Доходность к погашению облигации – Как посчитать доходность облигаций? — вопросы от читателей Т—Ж

Как определить текущую доходность облигации? — вопросы от читателей Т—Ж

У меня возник ряд вопросов по облигациям, в частности по ОФЗ 46020. Сразу предупрежу, что не обладаю глубокими знаниями по финансовым инструментам.

Вопросы следующие:

1. Что такое текущая доходность и почему она изменяется? Как может быть текущая доходность ниже установленной для бумаги, если бумага торгуется с дисконтом от номинала?
2. Почему доходность бумаги ниже установленной 8,28% и по сумме купонов за год составляет всего 6,88% от номинала?

Юрий

У облигаций есть несколько видов доходности. Какая доходность получится у инвестора — зависит от суммы купона, цены покупки и срока владения бумагой. Подробно мы уже описывали варианты в статье «Как посчитать доходность облигаций?».

Дмитрий Печников

частный инвестор

Разберем, чем купонная доходность отличается от текущей, когда текущая будет выше купонной, а когда — наоборот.

Купонная доходность

При выпуске облигации эмитент определяет размер купонов. Если разделить их сумму за год на номинал облигации, получится купонная доходность.

В ОФЗ 46020 величина всех купонов заранее известна. На каждую облигацию выплачивается 34,41 Р два раза в год. Если купить облигацию по номиналу 1000 Р, то доходность составит 6,9%. Считаем по следующей формуле:

34,41 × 2 / 1000 = 6,9%

Эта доходность установлена эмитентом — ее получит инвестор, если купит облигацию по номиналу. Но купить облигацию по номиналу можно не всегда.

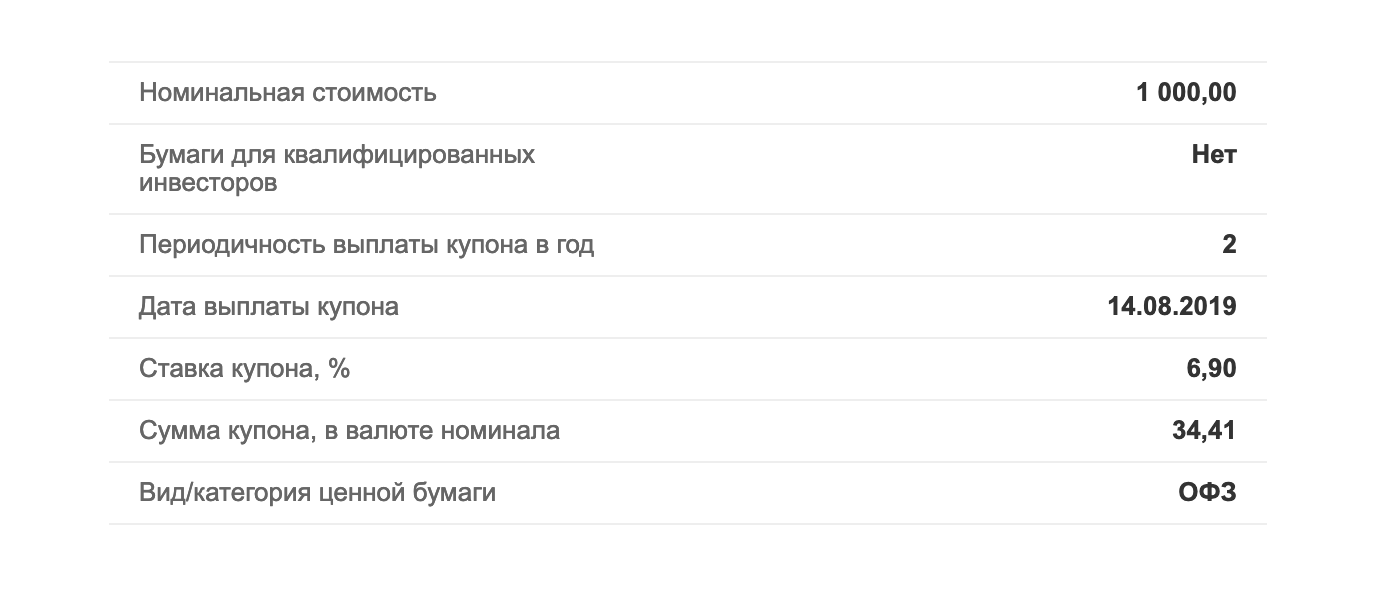Параметры ОФЗ 46020 на сайте Московской биржи

Текущая доходность

Те, кто купил облигацию у эмитента, могут продать ее на бирже по любой цене. Поэтому обычно рыночная цена облигации отличается от номинала. Величина купона, который будет получать новый владелец, при этом не меняется.

Если купить облигацию на вторичном рынке, доходность будет отличаться от купонной. Чтобы узнать насколько, нужно разделить сумму купонов на текущую стоимость облигации. Это и будет текущая доходность.

Сейчас на бирже ОФЗ 46020 можно купить дешевле номинала. Например, 5 марта 2019 года она стоила 870 Р.

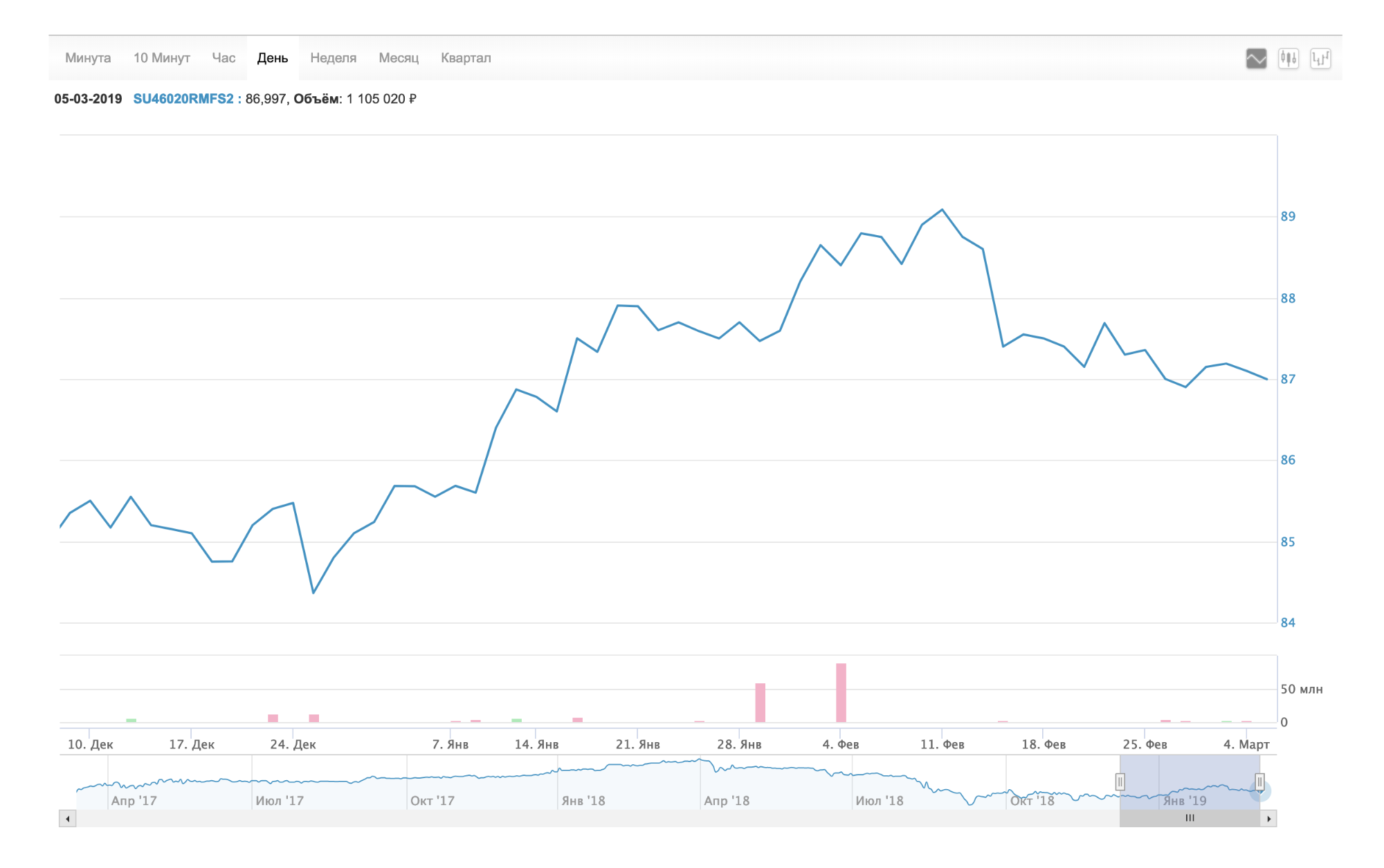График изменения цены ОФЗ 46020 на сайте Московской биржи

Размер купона тот же — 34,41 Р. Рассчитаем текущую доходность:

34,41 × 2 / 870 = 7,9%

Если цена облигации ниже номинала, то текущая доходность всегда выше купонной. И наоборот, если облигация торгуется дороже номинала, текущая доходность будет ниже купонной.

В своем вопросе вы сказали, что «установленная» доходность ОФЗ 46020 составляет 8,28%, но это не совсем так. На самом деле изначально установленной можно считать только купонную доходность — в этом случае это 6,9%. Соответственно, все изменения текущей доходности стоит смотреть относительно купонной доходности.

Для проверки представим, что ОФЗ 46020 стала стоить 1100 Р. Посчитаем текущую доходность в этом случае:

34,41 × 2 / 1100 = 6,3%

Как и ожидалось, получили доходность меньше купонной. Это обязательно нужно учитывать, если покупаете облигацию дороже номинала.

А зачем другие доходности?

Текущая доходность отражает только купонные выплаты. На итоговый доход от владения облигацией влияет еще и цена продажи или погашения.

Посчитаем, какой доход принесет ОФЗ 46020, если держать ее до погашения в 2036 году.

В конце срока действия эмитент обязан погасить облигацию по номиналу. Даже если вы купили ее за 870 Р, после погашения на счет поступит 1000 Р за каждую бумагу. Прибыль от продажи в этом случае составит 13%:

(1000 — 870) / 870 = 14,9%

Чтобы рассчитать годовую доходность, нужно разделить прибыль на срок владения облигациями:

14,9% / 6182 × 365 = 0,88%

Итоговая доходность — это сумма доходности от получения купонов и доходности от продажи:

Предполагаю, что доходность 8,28%, которую вы назвали установленной, на самом деле как раз и есть доходность к погашению: в ней учтены и купоны, и доход от погашения облигации по номиналу.

Все эти доходности необязательно считать самостоятельно. Все виды доходностей можно найти на сайтах с информацией по облигациям. Например, на rusbonds.ru, cbonds.ru или bonds.finam.ru.

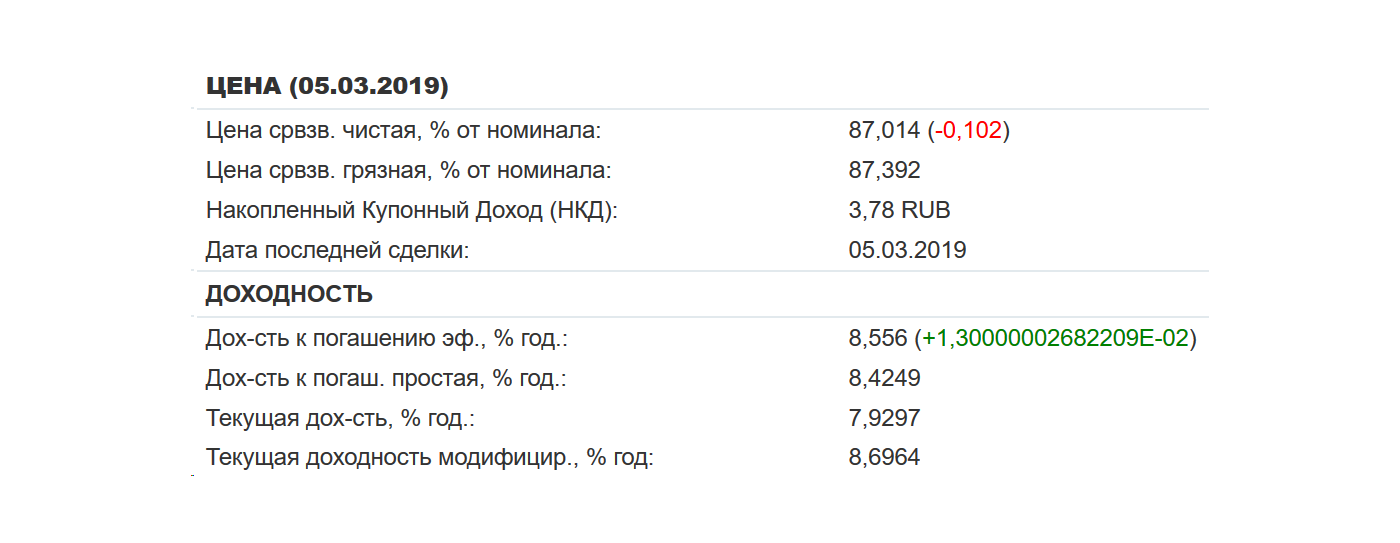Цена и текущая доходность ОФЗ 46020 на 05.03.2019. Источник: rusbonds.ru

В облигациях еще много нюансов. Про них можно почитать в нашей статье «Дать денег Минфину».

Если у вас есть вопрос об инвестициях, личных финансах или семейном бюджете, пишите. На самые интересные вопросы ответим в журнале.

journal.tinkoff.ru

Дюрация облигаций

Дюрация — это эффективный срок до погашения облигации. Простыми словами — это количество лет или дней, через которые инвестор вернет вложенные в облигацию деньги. Эффективный срок учитывает все купонные платежи, выплаченные в разное время, и различные особенности облигации, такие как амортизация или оферта. Если купонных платежей, амортизации и оферты нет, то дюрация совпадает со сроком до погашения облигации.

Юлия Семенюк

частный инвестор

Для чего нужна и где используется

С помощью дюрации инвесторы и аналитики измеряют средний срок возврата инвестиций. Дюрация показывает зависимость облигаций от изменения процентных ставок, и это полезно при выборе облигаций.

Также дюрация позволяет оценить другие финансовые активы с фиксированными выплатами. Например, банки могут рассчитывать дюрацию кредитов и кредитных портфелей.

Как узнать дюрацию

Необязательно считать самостоятельно: значение можно посмотреть на справочных сайтах, например в облигационном разделе «Смарт-лаба», на cbonds.ru или rusbonds.ru.

Но мы все же рассмотрим несколько методик расчета.

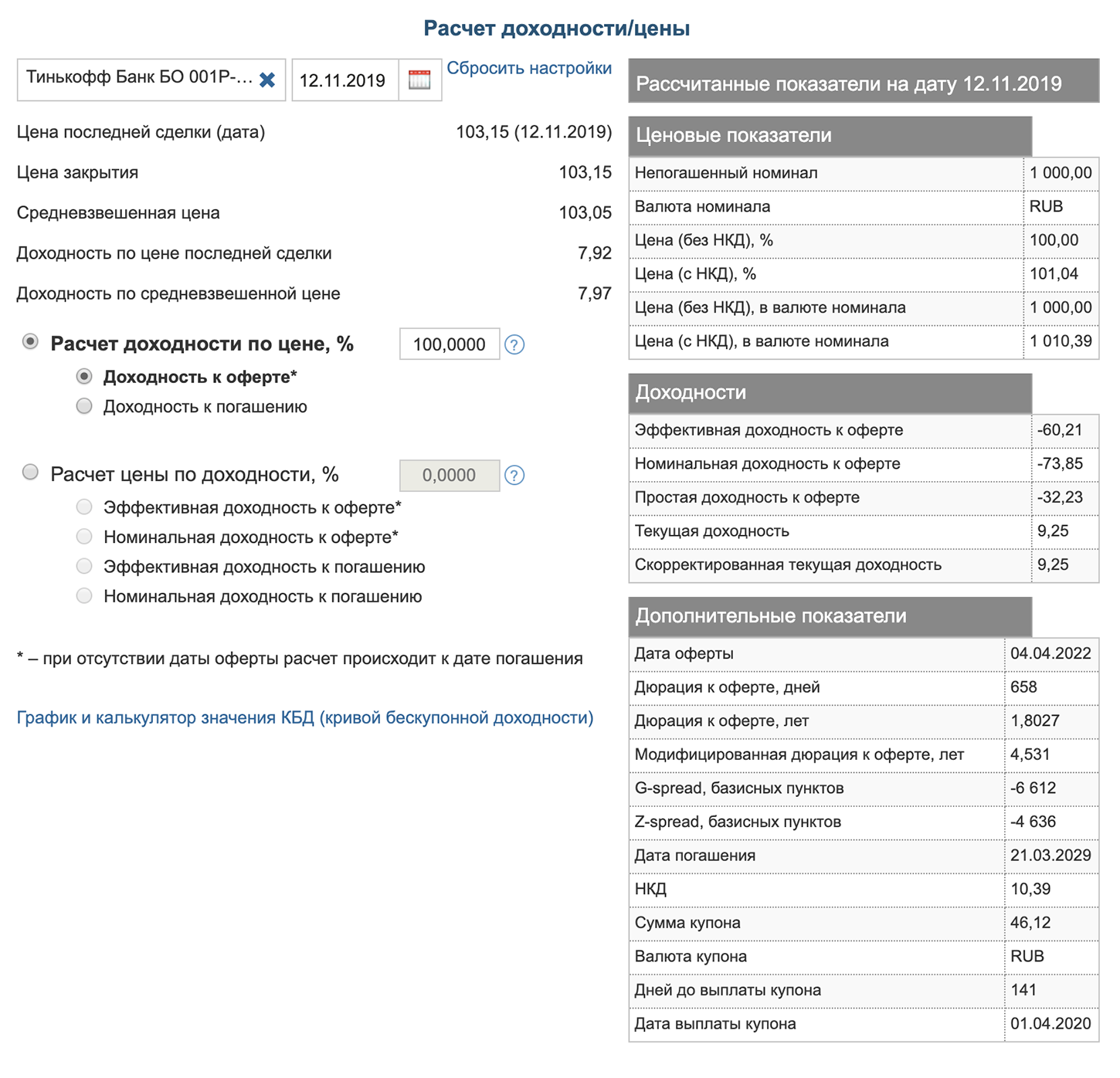Сведения об облигации Тинькофф 001Р-02R в калькуляторе на сайте Московской биржи. В правом нижнем углу — данные о дюрации

Дюрация Маколея: формула расчета

Первый и наиболее известный способ расчета дюрации — формула Маколея. Дюрация Маколея показывает эффективный срок до погашения облигации.

Чтобы рассчитать дюрацию, надо сложить все будущие платежи с учетом срока их поступления и поделить результат на рыночную цену облигации с учетом накопленного купонного дохода. Будущие платежи по облигации — это купоны и погашение номинала частями или в конце срока.

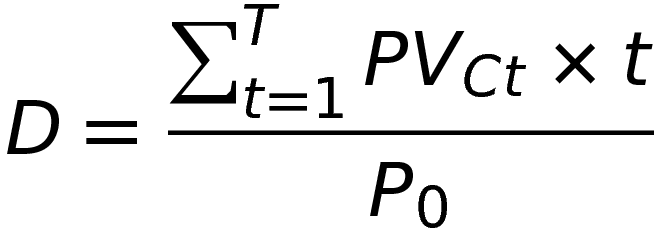
Пример расчета дюрации. Допустим, номинал и текущая цена облигации с учетом НКД равны 1000 Р, купон в 10% выплачивается раз в год. До погашения облигации осталось 4 года, доходность до погашения — 10%.

В числителе мы складываем все денежные потоки: четыре купонных платежа и погашение номинала облигации. Так как это будущие платежи разного времени, нужно каким-то образом привести их к сегодняшнему дню. С точки зрения математики эти платежи надо освободить от 10% доходности, то есть дисконтировать. Дисконтирование — это процесс, обратный начислению процентов. В нашем случае ставка дисконтирования — это годовая доходность, то есть 10%.

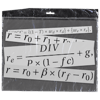
Что такое ставка дисконтирования

Далее надо поделить это на цену облигации с НКД — и мы получим дюрацию.

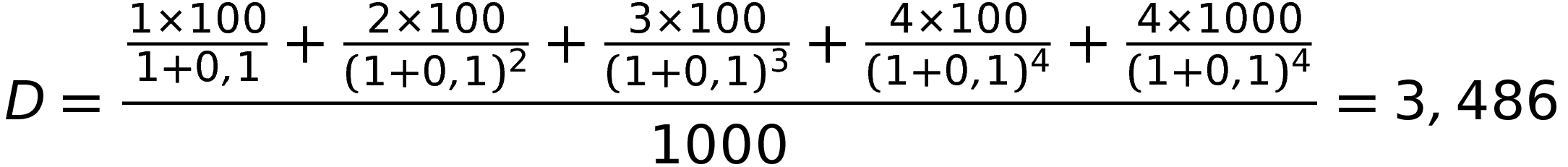
Если купоны выплачиваются чаще раза в год, то расчет усложнится. Квартальных или полугодовых платежей больше, и их надо дисконтировать по квартальной или полугодовой ставке.

Как вложиться и не облажаться

Расскажем в еженедельной рассылке для инвесторов. Подпишитесь и получайте письма каждый понедельник

Модифицированная дюрация

Модифицированная дюрация — это второй способ измерения дюрации. С ее помощью инвестор определяет, на сколько процентов изменится цена облигации, если изменятся процентные ставки.

MD = Дюрация Маколея / (1 + процентная ставка)

Для небольших изменений работает следующая формула:

Изменение цены / Рыночная цена с НКД = −MD × Изменение ставок

Например, MD равна 3, цена облигации с учетом НКД — 95%, доходность к погашению — 8% годовых. Мы можем определить, как изменится цена, если доходность вырастет на 0,5 процентного пункта и станет равна 8,5%.

Х / 0,95 = −3 × 0,005

Х = −3 × 0,005 × 0,95 = −0,01425

Если доходность вырастет на 0,5%, цена облигации снизится на 1,4%.

Эффективная дюрация и оферта

Эффективная дюрация — третий способ измерить дюрацию. Подходит для облигаций, которые содержат встроенные условия — то есть эмитент может их выкупить раньше срока погашения по оферте. Вероятность того, что облигация будет выкуплена, сокращает ее дюрацию.

Дюрацию облигаций с офертой рассчитывают по формуле эффективной дюрации:

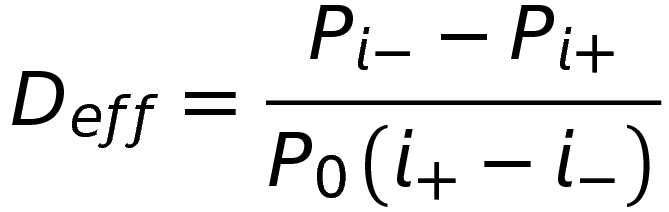
В числителе стоит разница между ценой облигации в условиях падения ставок и ее ценой при росте ставок. В знаменателе — первоначальная цена, умноженная на разницу ставок.

Например, у облигации Тинькофф 001Р-02R дюрация на 23 октября 2019 года составляет 674 дня, хотя срок обращения облигации — 3640 дней. Дюрация существенно меньше срока обращения, потому что по облигации предусмотрена оферта 4 апреля 2022 года и дюрация рассчитывается на момент оферты.

Дюрация портфеля облигаций

Дюрация портфеля облигаций — это средневзвешенная дюрация отдельных облигаций.

Например, в портфеле инвестора два вида облигаций — РЖД 001P-12R с дюрацией 1308 дней и ПИК БО-П03 с дюрацией 866 дней. Доли в портфеле — 70 и 30% соответственно.

Как я выбираю корпоративные облигации

ДПорт = 1308 × 0,7 + 866 × 0,3 = 915,6 + 259,8 = 1175,4 дня

Дюрация проекта

По экономическому смыслу дюрация проекта близка к показателю срока окупаемости проекта, но она учитывает только дисконтированные денежные потоки и не учитывает размер инвестиций.

Формула дюрации проекта:

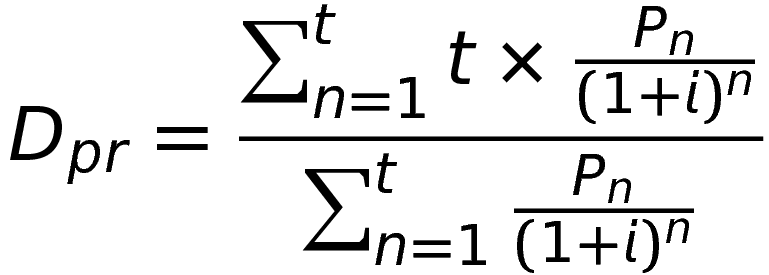
Например, есть проект, который принесет по 500 Р в четвертый и пятый годы существования. Ставка дисконтирования зависит от многих факторов, например от риска инвестиций. В данном случае она составляет, допустим, 20%. Скорее всего, проект рискованный, поэтому по нему предлагают доходность выше, чем по надежным банковским депозитам. Рассчитаем дюрацию этого проекта.

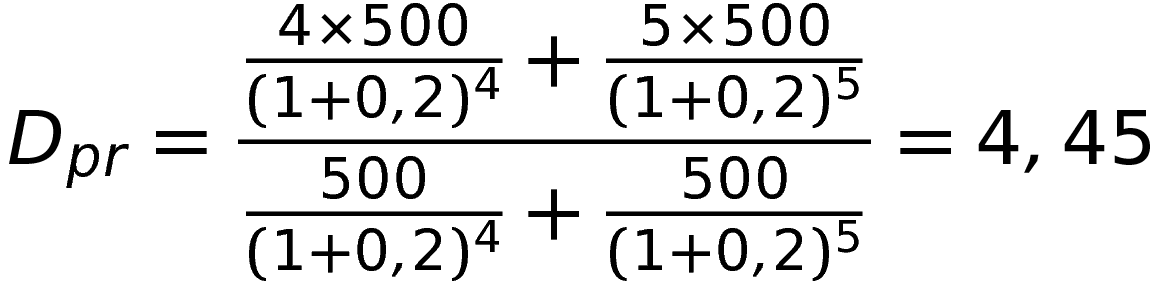
Таким образом, без учета первоначальных вложений проект окупится через четыре года и пять с половиной месяцев.

Свойства дюрации

Дюрация купонных облигаций меньше времени до погашения, потому что инвестор регулярно получает купонные платежи.

Дюрация дисконтных облигаций равна времени до погашения, потому что по дисконтным облигациям инвесторы не получают купоны. Если купон один и выплачивается при погашении, дюрация также будет равна сроку до погашения.

При прочих равных чем меньше купон по облигации, чем реже его выплачивают или чем больше времени до погашения, тем больше дюрация: инвестор будет дольше возвращать свои деньги. И наоборот: если купонные платежи большие и более частые, а времени до погашения немного, то дюрация будет меньше, потому что инвестор быстрее вернет свои деньги.

Если рыночная цена облигации падает, то ее доходность растет и дюрация уменьшается, потому что инвестор покупает облигацию дешевле и возвращает вложения быстрее. И наоборот: если рыночная цена облигации растет, то ее доходность падает, а дюрация увеличивается, потому что инвестор больше платит за покупку и медленнее возвращает вложенные деньги.

Что делать? 03.10.18

Как посчитать доходность облигаций?

Зависимость от процентных ставок

Если купонные платежи по облигациям зафиксированы, то риск для инвесторов заключается в колебаниях цены облигации. Цена облигации и процентные ставки связаны обратной зависимостью: если процентные ставки в экономике растут, то цена ранее выпущенных облигаций падает, и наоборот.

Чем меньше дюрация, тем меньше цена облигации изменится при изменении процентных ставок. Например, по облигациям Тинькофф БО-07 на 23 октября 2019 года дюрация всего 64 дня, потому что 30 декабря банк погасит облигации по номиналу. Скорее всего, за оставшиеся несколько месяцев цена облигации практически не поменяется.

И наоборот: чем выше дюрация, тем больше вероятность того, что цена облигаций существенно изменится при изменении процентных ставок. Например, по облигациям РЖД 001P-12R на 23 октября дюрация составляет 1308 дней, или 3,6 года. За несколько лет ставки могут измениться, а значит, и цена облигации изменится.

Что такое выпуклость облигаций и как она связана с дюрацией

Зависимость цены облигации от ее доходности не линейная, а выпуклая. Выпуклость облигаций бывает позитивной и негативной, а точное значение выпуклости для конкретных облигаций можно посмотреть на rusbonds.ru. В некоторых источниках выпуклость называют конвекцией.

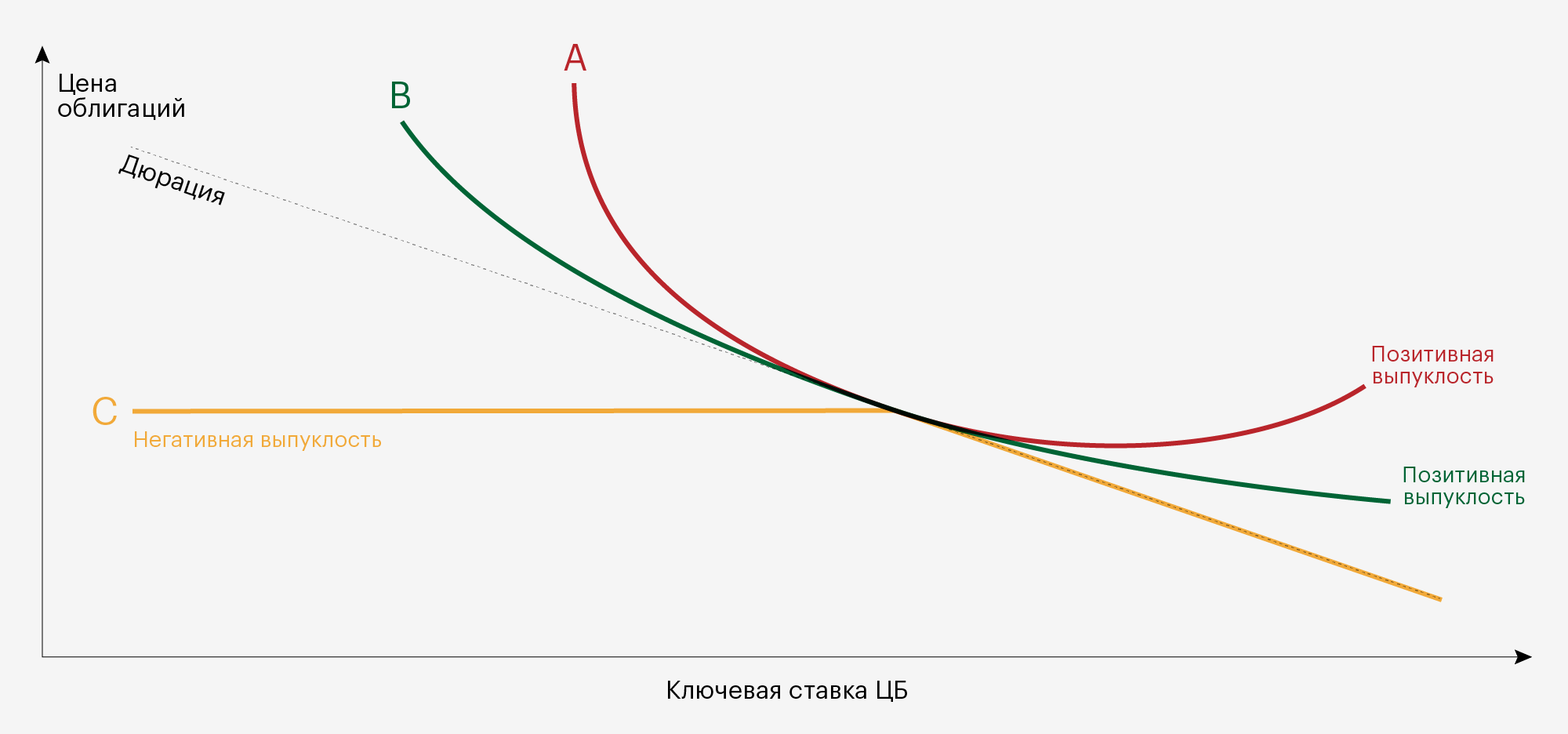Красная и зеленые линии — графики цены двух облигаций с позитивной выпуклостью. Желтая линия — график цены облигации с негативной выпуклостью. Пунктирная линия — дюрация облигаций. Выпуклые линии отклоняются от пунктирной линии при изменении процентных ставок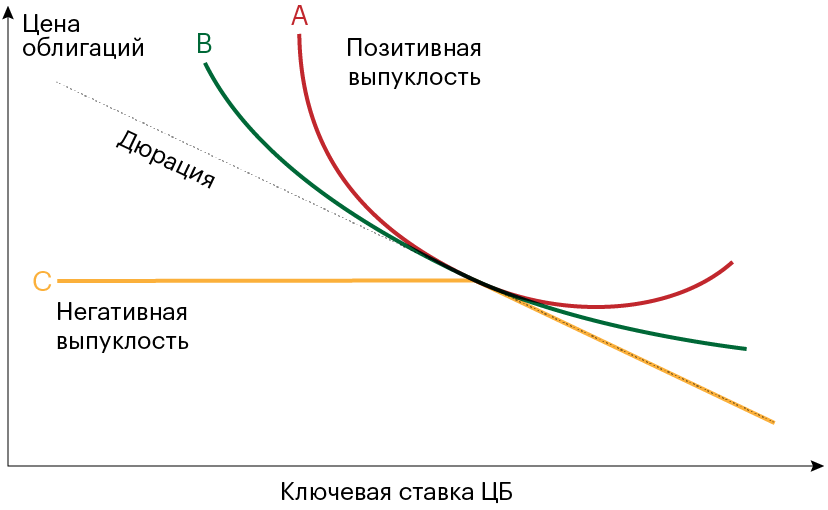Красная и зеленые линии — графики цены двух облигаций с позитивной выпуклостью. Желтая линия — график цены облигации с негативной выпуклостью. Пунктирная линия — дюрация облигаций. Выпуклые линии отклоняются от пунктирной линии при изменении процентных ставок

На графике цена облигации C с негативной выпуклостью — желтая линия — при росте ставки меняется, а при падении ставки остается стабильной. Оценка таких облигаций с помощью дюрации дает очень большую погрешность из-за асимметрии между ценой и доходностью облигации. На графике асимметрия — это расстояние между пунктирной и сплошными линиями, которое увеличивается из-за выпуклости. Поэтому при больших изменениях процентной ставки используют выпуклость.

Профессиональные управляющие используют выпуклость для оценки инвестиционных портфелей. Частным инвесторам выпуклость может быть полезна, если дюрация облигаций одинаковая.

На рисунке дюрация двух облигаций с позитивной выпуклостью — красная и зеленая линии — одинаковая, но выпуклость облигации А больше, чем у облигации В. При падении ключевой ставки ЦБ цена облигации А вырастет больше, чем цена облигации В. При росте ключевой ставки ЦБ цена облигации А упадет меньше, чем цена облигации В. Таким образом, более выпуклая облигация А выгоднее для инвестора.

Что делать? 08.08.19

Как ставка ЦБ влияет на доходность облигаций?

Как применять дюрацию на практике

На практике с помощью модифицированной дюрации вычисляют, как изменится цена облигации при изменении рыночных процентных ставок.

Например, доходность облигации к погашению — 12%, а модифицированная дюрация — 3,469. Мы можем определить, как изменится цена облигации при росте рыночных ставок на 1%:

−3,469 × 0,01 / 1,12 = −0,031 = −3,1%

При росте ставок на 1% цена этой облигации снизится на 3,1%.

С помощью обычной дюрации инвесторы сравнивают похожие облигации и выбирают ту, у которой дюрация меньше. Так можно уменьшить процентный риск.

Например, у облигаций Мегафон БО-001Р-03 и МТС 001P-01 по 10 купонных периодов и одинаковый срок обращения — 1820 дней. Но у облигаций МТС купон равен 44,88 Р, а у облигаций «Мегафона» — 39,14 Р. Соответственно, дюрация у облигаций МТС — 836 дней, а у бумаг «Мегафона» — 1016. При других похожих параметрах инвестору безопаснее купить облигации с меньшей дюрацией.

Если инвестор полагает, что процентные ставки в экономике будут снижаться, разумно купить облигации с большим сроком погашения и, соответственно, большей дюрацией. Цена таких облигаций вырастет, а кроме того, по ним по-прежнему будут выплачиваться более высокие купоны, чем по новым облигациям.

Напротив, если ожидается повышение процентных ставок, облигации с меньшей дюрацией могут оказаться более подходящими, так как их цена снизится в меньшей степени.

Использование дюрации для оценки риска облигаций. Чтобы уменьшить процентный риск, инвестор выбирает облигации с низкой дюрацией или формирует портфель с заданной дюрацией.

Как измерить риск инвестиций

Например, инвестор хочет составить портфель из двух видов облигаций — с дюрациями 3,4 и 5,6 года — и застраховаться от риска изменения процентных ставок на 5 лет. Инвестор не может повлиять на изменение рыночных процентных ставок, но на время дюрации он получает гарантированный купонный доход. Если рыночные ставки растут, то цена облигаций падает. Инвестор реинвестирует купоны под более высокий процент и этим компенсирует падение цены облигации. Таким образом, для страхования риска инвестор должен составить портфель с дюрацией 5 лет и определить доли облигаций.

Доля облигаций А + Доля облигаций В = 100%

Дюрация портфеля = Доля А × 3,4 + Доля В × 5,6 = 5 лет

Доля облигаций А = 27%

Доля облигаций В = 73%

Эта техника называется иммунизацией портфеля, и она работает для небольших изменений процентных ставок.

journal.tinkoff.ru

Доходность к погашению (Yield to maturity, YTM)

Давно хотел понять, что такое доходность к погашению, но всё никак руки не доходили. Одно дело, когда тебе квик/сайт ММВБ показывает какое-то число, типа 5.25%, и вроде оно и должно быть правильным, но что за этим стоит? И что это означает на практике? В инете есть сложные формулы доходности, и (если сможешь разобраться) они вроде считают приблизительно то же самое, но, опять же, почему они именно такие, как они получены? Хочется, чтобы этот процент, какой бы он ни был, можно было напрямую сравнивать со ставками банковских вкладов, потому что это просто и понятно.

Зачем нужно уметь считать доходность самому? 

1. Чтобы проверить, что она на самом деле такая.
2. Чтобы учесть налог на купон для корпоративных бумаг, т.к. в квике он не учитывается.
3. Чтобы учесть комиссию.
4. Чтобы посчитать доходность для бумаг, по к-м нет торгов на бирже (есть на внебирже) и поэтому в квике показывается 0.
5. Можно посчитать для любой цены или даты.

Сразу скажу, что самый простой способ посчитать доходность – это использовать функцию ДОХОД в Excel. Для примера я буду использовать еврооблигацию GAZPR-34 на 10.01.18 с ценой 137.5 и НКД 17,7292. В данном случае ф-я ДОХОД получает 4,284% (тут учитывается налог), но при этом она требует очень мало параметров:

ДОХОД(дата покупки; дата погашения; ставка купона; цена;100; 2; 0)*100.

НКД она считает сама. Есть и отдельная функция для подсчета НКД — НАКОПДОХОД(). Кроме того, в Excel есть и другие функции, к-е могут оказаться полезными:
ДАТАКУПОНДО/ДАТАКУПОНПОСЛЕ – определяют дату предыдущего/следующего купона
ЧИСЛКУПОН — число оставшихся купонов. 

Сначала я (наверное, как и многие) предполагал, что тут весь фокус в капитализации и реинвестировании купонов, и даже стал считать таким образом доходность в Excel. Цифры получались близкие к тем, что показывал квик, но всё же не те, тем более, что по некоторым бумагам они отличались значительно.

Затем я придумал интервальный способ подсчета, в котором весь период времени до погашения разбивается на интервалы длиной полгода (между купонами), и доходность считается для каждого из них, а затем получается средневзвешенная дох-ть для всего периода. Здесь делается предположение, что цена с момента покупки до погашения равномерно снижается (или увеличивается) до номинала. Зная количество дней до погашения и текущую цену, можно получить предполагаемое изменение цены за 1 день, и за любое число дней, а значит – и в день выплаты каждого купона. А зная последние, можно для каждого интервала получить:

• Сумма вначале (цена)
• Сумма в конце (цена в конце + купон)
• Разница, процент и годовой процент

Для самого 1-го периода ситуация несколько усложняется НКД, но это не принципиально. Далее, получив для каждого интервала годовой процент и зная цену в его начале, можно получить средневзвешенный годовой процент за всё время (используя цену как вес т.к. она всё время меняется). Полученное значение уже больше похоже на то что показывает квик, но и оно немного отличается. Проблема в том, что оно начинает заметно меняться, когда от даты покупки до первого купона остается мало времени, особенно, если учесть комиссию. Причина оказывается в том, что т.к. длина интервала в днях тоже разная её тоже надо учитывать как вес. При добавлении её в расчеты результат перестает зависеть от длины первого интервала. В Excel всё это выглядит примерно так (здесь не учитывается НДФЛ):

Проблема с этим способом состоит в том, что он основан на предположении, что цена идет к номиналу равномерно, а в реальности это не так, и в идеале определение доходности от цены зависеть не должно.

В какой-то момент попался пост на эту тему anatolyutkin «Еврооблигации и депозиты», к-й дал подсказку. На самом деле там всё написано, но т.к. у меня в финансовой области образования нет, то я его сразу осилить не смог, тем более что там в расчётах используется Бином Ньютона и т.п., но всё же я понял основную идею – текущая стоимость. Оказывается, это такой финансовый термин, к-й означает сколько нужно вложить сегодня, чтобы через какое-то время получить заданную сумму. Фокус в том, что обычно расчет производится наоборот – имеем сумму, например 1000р, процент (8%), и через год получаем 1080р. А здесь известно, сколько будет в конце и процент, а найти надо, сколько было вначале.

Ну а дальше основной финт мозгами состоит в том, чтобы понять, что когда вы покупаете облигацию (затраты = текущая цена + НКД), вы как бы открываете много маленьких вкладов на разные сроки. Вкладов столько, сколько вы получите купонов + еще 1 для номинала. Каждый вклад закрывается, когда вы получаете по нему купон, и все вклады имеют одинаковый процент.

Но здесь есть 1 нюанс – считать нужно так, как будто эти вклады имеют капитализацию. Её на самом деле конечно нет, но это нужно делать для того, чтобы полученный процент соответствовал каким-то общепринятым ориентирам. Если нам нужно сравнить доходность с обычными вкладами, то можно использовать годовую капитализацию. С другой стороны,

In a number of major markets (such as gilts) the convention is to quote annualised yields with semi-annual compounding

Что означает, что существует соглашение указывать доходность с полугодичной капитализацией, так что можно посчитать и так. Понятно, что из-за более частой капитализации процент доходности будет немного ниже. В квике, на сайте ММВБ и в функции ДОХОД доходность вычисляется именно так. Формула для расчета начальной суммы отдельного вклада для годовой капитализации выглядит так:

Sum=EndSum / ((1+Rate/100)^Years) / (1+Rate/100*YearPart)

Здесь EndSum – купон или номинал, Rate – искомый процент, Years — число полных лет вклада, YearPart – дробная часть лет. Для полугодичного варианта:

Sum=EndSum / ((1+Rate/200)^YearHalves) / (1+Rate/100* YearHalfPart)

Здесь YearHalves – число полных полугодий, YearHalfPart — дробная часть полугодий. Далее, если просуммировать все начальные суммы этих вкладов, то должно получиться число, равное первоначальным затратам, т.е. текущая цена + НКД. Другими словами, тут нельзя получить формулу типа Rate=… где доходность вычисляется одним выражением – нужно подбирать разные значения до тех пор, пока результат не будет отличаться от требуемого на величину типа 0.00001. В Excel это выглядит так (здесь НДФЛ уже учтен, при этом для простоты в НКД он тоже учтён):

Конечно, так рассчитывать доходность не нужно, это просто для понимания. В интернете также можно найти более простые формулы для расчета доходности без суммирования, в к-х присутствует параметр «общее количество купонных платежей», но при этом не учитывается НКД. Кроме того, на сайте ММВБ есть документ «Методика расчета НКД и доходности», содержащий формулу доходности с параметром «число дней». Этот параметр делится на число дней в году, т.е. получается число лет, т.о., данная формула получает доходность с годовой капитализацией, и это не та величина, к-я показывается на этом же сайте для конкретных бумаг.

Еще раз скажу про заблуждение насчет реинвестирования – оно в расчете ДП не учитывается:

A common misconception is that the coupons must be reinvested at the yield to maturity… making this assumption is a common mistake in financial literature and coupon reinvestment is not required for YTM formula to hold.
(Вики)

It is a chronic error in that it persists in spite of continued attempts to correct it. For example, Renshaw addressed this error fifty years ago … but the reinvestment assumption continues to be replicated. … successive generations of financial professionals educated with the erroneous text have restated the claim in materials intended to educate investors….

Among the sites containing this claim are Bloomberg.com,… Investopedia.com, Morningstar.com, and even the popularly edited Wikipedia.org…
(«Yield-to-Maturity and the Reinvestment of Coupon Payments»)

Получаемая величина ДП, например 4.3%, означает только процент, к-й начисляется на вложенные средства только пока вы владеете данной ЦБ. Как только вы получили деньги (купон) назад, этот процент начисляться перестает а его новые инвестиции к нему никакого отношения не имеют. Разница только в том, что в случае обычного вклада вы получаете сразу всю сумму назад с процентами, а здесь как бы есть много маленьких вкладов под одинаковый процент и вы получаете их по одному постепенно.

Т.к. нам более привычна ситуация когда вся сумма возвращается сразу, можно попытаться посчитать и т.н. реальную доходность с учетом последующего (ре)инвестирования купонов (необязательно в ту же ЦБ) до погашения. Для каждого купона срок его реинвестирования равен

ReinvDays=EndDate-CouponDate

где EndDate – дата погашения и CouponDate – дата выплаты купона. Сумма, к-я получается в результате реинвестирования купона рассчитывается по формуле:

ReinvSum = Coupon * ((1+ReinvRate/100)^ReinvYears) * (1+ReinvRate/100*ReinvYearPart)

(здесь подразумевается ежегодная капитализация). Если просуммировать все такие суммы, а также последний купон и номинал, то получится итоговая сумма за весь срок до погашения. Зная начальную (Sum1=цена + НКД) и конечную сумму EndSum, а также срок, можно подобрать ставку, к-я даст такой результат, используя ту же формулу:

EndSum = Sum1 * ((1+RealRate/100)^TotalYears) * (1+RealRate/100*TotalYearPart)

Очевидно, что на практике реинвестировать под ту же ставку не получится, поэтому можно просто рассмотреть разные варианты для оценки. Для того же примера с ДП = 4,3263%:

• Если ReinvRate=0 (купоны вообще не инвестируются), то RealRate=2,96%
• Если ReinvRate=3%, то RealRate=3,876%
• Если ReinvRate=Rate=4,3263%, то реальная дох-ть будет такой же
• Если ReinvRate=5%, то RealRate=4,567%

Как видим, ставка реинвестирования влияет на итоговую реальную доходность.

smart-lab.ru

Можно ли заработать 10% в год на облигациях? — вопросы от читателей Т—Ж

Можно ли вывести облигации на постоянный денежный поток — за счет купонного дохода — с доходностью до 10% в год? Неважно, какие облигации: корпоративные, государственные или и те и другие вместе. И как ЦБ может повлиять на доходность облигаций?

Рамиль

Облигации — полезный финансовый инструмент. Их доходность определена заранее и обычно выше, чем у вкладов. Сейчас средняя ставка по депозитам в надежном банке немного меньше 7,75%. На облигациях можно заработать и 10%, и даже больше. Но нужно помнить, что чем больше доходность, тем выше риск потерять деньги.

Дмитрий Печников

частный инвестор

По каким облигациям можно получить 10%

Посмотрим, как доходность облигации зависит от надежности эмитента. Будем считать, что после покупки бумаги удерживаются до погашения. Чтобы доходность была постоянной на весь срок действия, величина купона должна быть зафиксирована заранее. Будем искать облигации с текущей доходностью к погашению выше 10%.

Начнем с государственных облигаций — самых надежных. Сейчас наибольшая доходность у ОФЗ 26225 с погашением в 2034 году — 8,4%. Не 10%, но и риск потерять деньги минимален.

Что делать? 03.10.18

Как посчитать доходность облигаций?

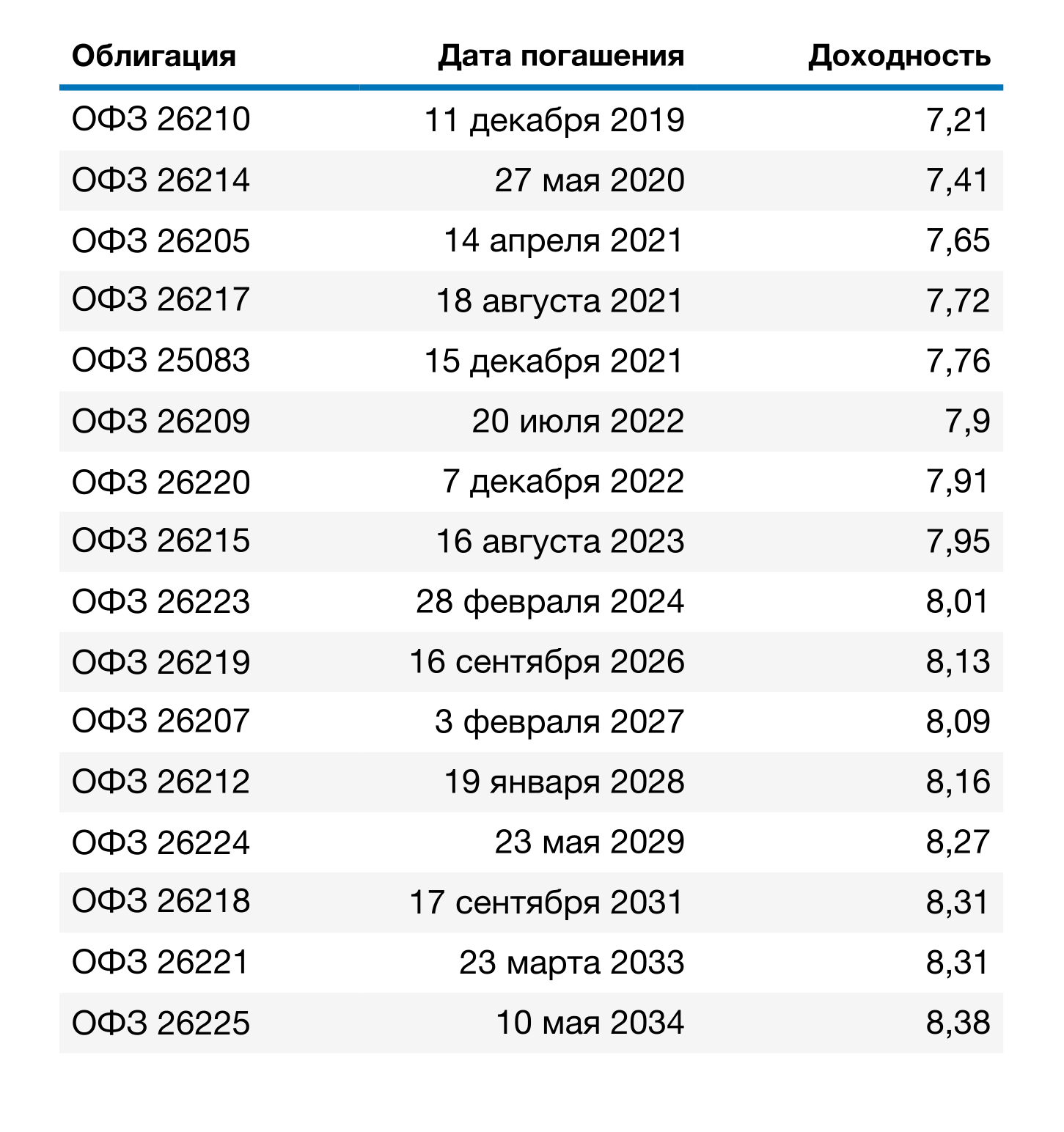Доходность к погашению ОФЗ в зависимости от срока действия. Данные с сайта Московской биржи

Корпоративных облигаций гораздо больше, чем государственных. На них можно заработать даже 15% годовых. Но и риск банкротства компании выше, чем у государства. Чтобы было проще выбрать надежного эмитента, можно использовать кредитные рейтинги.

Существуют рейтинговые агентства, которые оценивают риск банкротства эмитентов. Они присваивают кредитный рейтинг, который показывает, насколько рискованно давать в долг компании или государству. Известные международные агентства: Standard & Poor’s, Moody’s и FitchRatings, российские: АКРА и «Эксперт РА». Используя их данные, можно быстро оценить платежеспособность эмитента. Например, кредитный рейтинг компании «Окей» — ruA−, а «Обуви России» — ruBBB+. Значит, первый с большей вероятностью сможет платить по долгам.

Шкала кредитных рейтингов агентства «Эксперт РА»

Кредитный рейтинг есть не у всех компаний. Это не значит обязательно, что эмитент ненадежный, но требует времени на самостоятельную оценку его финансового положения. Если нет желания этим заниматься, лучше сделать выбор в пользу компании с известным рейтингом.

Как пример облигации с требуемой доходностью и неплохим кредитным рейтингом — ФПК Гарант-Инвест-001Р-05.

О чем еще важно помнить при покупке облигаций

Доходность к погашению подразумевает, что вы не продадите бумаги раньше даты погашения. У бумаг с устраивающей вас доходностью может быть очень далекая дата погашения — 5 или 10 лет. Если вы продадите бумаги до погашения, не факт, что реальная доходность получится на ожидаемом уровне.

Эффективная доходность к погашению учитывает реинвестирование. На практике это значит, что заявленной доходности получится достичь, если на все полученные купоны тут же покупать облигации с такой же доходностью. И если тело облигации постепенно амортизируется, вырученные деньги также нужно реинвестировать. В реальности это не всегда может получиться: к моменту выплаты купонов или амортизации бумаг с нужной доходностью может просто не оказаться в продаже.

В доходности не учтены комиссии брокера. Их нереально учесть, потому что у каждого брокера свои условия. Особенно важно помнить об этом при покупке бумаг с коротким сроком — комиссия может ощутимо повлиять на реальную доходность. Также, если вы рассчитываете держать облигации до оферты, а не до погашения, важно помнить, что за выставление оферты брокеры могут брать дополнительную комиссию.

Как ЦБ может повлиять на доходность облигаций

Центральный банк России устанавливает ключевую ставку: она определяет, под какой процент коммерческие банки могут получить деньги в кредит. Доходность облигаций напрямую зависит от ключевой ставки. Выше ставка ЦБ — выше доходность облигаций, и наоборот.

После того как вы купили облигации, ЦБ может повысить ставку. Инвесторы захотят скидку, и стоимость бумаг на бирже понизится — они могут торговаться дешевле номинала. Чтобы не получить убыток при продаже, можно держать облигации до погашения. В конце срока действия эмитент погасит их по номиналу, и вы получите ожидаемую доходность.

Если ЦБ понизит ставку, произойдет обратное: облигации подорожают, а их доходность понизится. В этот момент можно продать их и получить дополнительную доходность. Но нужно помнить, что вложить полученную прибыль в облигации с такой же высокой доходностью станет сложнее. Если текущий доход вас устраивает, лучше просто держать бумаги до погашения.

Выше я писал, что гособлигаций с доходностью 10% нет. Дело в том, что доходность ОФЗ обычно ненамного отличается от ключевой ставки. Сейчас ставка ЦБ составляет 7,75%. Если она вырастет, например, до 10%, будет легко найти облигации с такой доходностью, даже ОФЗ. С другой стороны, это будет означать повышенную инфляцию и пониженную реальную доходность вложений.

Помните о рисках

Сейчас 10% можно получить по облигациям компаний с кредитным рейтингом BBB+ и выше. У таких эмитентов достаточно высокая платежеспособность — значит, и дефолт менее вероятен. И все же риски вложений в корпоративные облигации выше, чем в ОФЗ или в региональные. Чтобы снизить вероятность потери денег при банкротстве эмитента, можно использовать несколько правил.

Корпоративные облигации
на Московской бирже

Не гнаться за доходностью. Чем надежнее компания, тем проще ей получить заем по низкой ставке и не выпускать облигации с большим купоном. Поэтому в большинстве случаев работает закономерность: чем ниже доходность облигаций, тем надежнее компания. Если для достижения финансовых целей вам достаточно 10%, сначала стоит посмотреть на облигации именно с такой доходностью.

Покупать облигации разных эмитентов вместо одного. Диверсификация вложений помогает не потерять всё при банкротстве конкретной компании. Для этого необязательно выбирать всех эмитентов самостоятельно — можно вложиться в ETF. Подробнее о том, как это работает, можно почитать в нашей статье.

Посмотреть, сколько денег у компании. Каждый эмитент раз в квартал рассказывает о своих финансах. Сколько зарабатывает и тратит, сколько на счете своих денег и заемных и так далее. Чтобы оценить компанию, прочитайте ее финансовую отчетность. Если прибыль в ней покрывает платежи по процентам, а долгов меньше, чем собственного капитала, у эмитента вряд ли возникнут проблемы с платежами.

Если у вас есть вопрос о личных финансах, правах или законах, пишите. На самые интересные вопросы ответим в журнале.

journal.tinkoff.ru

Доходность облигаций – их типы и формулы расчета

Доходность облигаций это параметр, который отражает прибыльность той или иной бумаги и обычно выражается в процентах годовых. Вообще доход по облигациям может быть двух типов:

1. Ежегодные купонные платежи;
2. Разница в цене (купил дешевле номинала, а в дату погашения реализовал облигацию по номиналу).

В связи с этим существует множество формул, по которым рассчитывается доходность облигаций, и разные формулы по-разному учитывают типы доходов, перечисленные выше. Обычно в облигационном калькуляторе имеют место четыре основные доходности, которые мы подробно рассмотрим в этой статье и проясним, что означает каждая из них.

Все виды доходностей, которые мы будем рассматривать, рассчитываются автоматически и инвесторам предлагаются уже в виде готового результата (не важно где, либо в терминале Квик, либо в облигационном калькуляторе, либо где-то еще). Но я все равно приведу формулы расчета данных показателей для более глубокого понимания сути вопроса.

1. Текущая доходность облигаций

Учитывает только выплату текущего купона. Например, облигация с номиналом 1000р. торгуется по 90%. Купонная дох-сть составляет 12% или 120р. в год. Следовательно, текущая дох-сть будет равна 120р./900р. = 13,33%.

Экономический смысл данной доходности в том, чтобы показать инвестору сколько процентов он будет получать в виде купонных выплат в зависимости от вложенных средств. То есть, когда человека интересует именно денежный поток без учета выплаты номинала в дату погашения, тогда нужно смотреть на это значение.

В этой цифре не учитывается тот факт, что приобрели вы облигацию по 90%, а погашать будете по 100%. Допустим, рассмотренная выше облигация погашается через 5 лет. Разница 10% между покупкой 90% и погашением 100% безусловно увеличит вашу итоговую доходность, но это произойдет только к концу срока погашения, а каждый год вы будете получать именно вот эту текущую дох-сть, которая в нашем примере равна 13,33%.

2. Текущая доходность модифицированная

В данной доходности учитывается и доход от разницы в цене и купоны. Данный тип не совсем корректен, т.к. полученное значение необходимо делить на количество лет, в течение которых мы владеем бумагой. Практического использования данная формула не имеет, однако во всех калькуляторах она есть, поэтому знать ее тоже нужно.

3. Простая доходность облигаций к погашению

В данной формуле учитывается прибыль и от покупки ниже номинала и купонные платежи. Например, облигацию мы купили по 90%, купон 12%, текущая дох-сть 13,33%, срок до погашения 4 года, т.е. за 4 года мы получаем 10% в виде разницы (100%-90%). Разделив эти 10% на 4 года, получаем 2,5% годовых, которые прибавим к 13,33% и получим простую дох-сть к погашению 15,83%. Однако, чем длиннее срок до погашения, тем сильнее доход от разницы размывается в годовой доходности. Так, при сроке 10 лет простая дох-сть будет эквивалентна 14,33%.

Используя данный показатель, облигации уже можно сравнивать между собой. Если при инвестировании вы планируете держать облигации до конца срока их обращения, при этом намерены забирать купоны себе, т.е. не реинвестировать купонный доход в эти же бумаги, то смотреть нужно именно на простую доходность облигаций.

4. Эффективная доходность

Если же вас интересует абсолютная доходность с учетом всей возможной прибыльности (т.е. купонные выплаты, разница в цене, а также прибыль от реинвестирования купонных платежей), тогда смотреть нужно на эффективную доходность облигаций.

Данный тип доходности является самым полным, именно это значение применяется биржей и транслируется в программе Квик в столбце «Доходность облигаций». Еще раз… данный тип доходности помимо купонных платежей и разницы в цене учитывает реинвестиции купонного дохода в те же самые облигации.

Как показывает практика, 95% инвесторов реинвестируют купоны, поэтому данную дох-сть приняли в качестве основного ориентира прибыльности облигаций. Помимо этого на базе указанного значения строится кривая доходности по облигациям.

Таким образом, мы рассмотрели типы доходностей облигационного рынка. Самой главной является эффективная доходность облигаций, она отражается в программе QUIK и именно ее использует биржа для расчета. На базе данного значения облигации можно сравнить друг с другом, и это даст ясную картину того, какая бумага более привлекательна для инвестиций с точки зрения возможной прибыльности.

stock-list.ru

Простая доходность облигации | Excel для финансиста

Простая доходность облигации — это доходность, рассчитанная в %годовых и зависящая от суммы купонного дохода по облигации и разницы в стоимости самой облигации в моменты покупки и продажи. От эффективной доходности отличается тем, что в расчёт не принимается возможность реинвестирования полученного купонного дохода в данную облигацию.

Считаю, что

простую доходность облигации уместно использовать, если выбранный срок инвестирования в облигацию невысок (например, до 2 лет) и сумма инвестирования невелика. В таком случае полученного купонного дохода просто не хватит для реинвестирования, и эффективную доходность считать нет смысла.

В данном примере разберём расчёт простой доходности облигации к погашению на примере одной из популярных государственных облигаций (ОФЗ)  ОФЗ-26218-ПД. Расчёт других облигаций (муниципальных и корпоративных) ничем принципиально не отличается от расчёта доходности ОФЗ.

Пример представлен для случая покупки ОФЗ через брокерскую контору, принцип расчёта доходности так называемых «народных ОФЗ«, приобретаемых через банки, немного другой (есть дополнительные комиссии и условия досрочного возврата) и будет рассмотрен отдельно.

Для расчёта необходимо знать следующие данные:

• номинал облигации (с учётом прошедшей амортизации),
• дату погашения облигации (в этом простом примере не будем рассматривать доходность к оферте),
• ставка купонов (в % годовых),
• сколько купонов в год выплачивается (при равномерной выплате),
• дату последнего выплаченного купона,
• текущая рыночная цена (в % от номинала).

Всю эту информацию можно найти на специализированных сайтах типа rusbonds.ru, cbonds.info, bonds.finam.ru и многих других.

Итак, расчёт простой доходности облигации к погашению ОФЗ-26218-ПД. Это облигация подходит для простого расчёта, так как есть постоянная доходность (размер купона не меняется) и нет амортизации (то есть номинал неизменен). Для случаев амортизируемых облигаций и переменных купонов лучше использовать другие способы, которые рассмотрим отдельно.

В первых строках размещена общая информация об облигации. В ячейке С7 рассчитывается срок до погашения простой формулой «

=C6-СЕГОДНЯ()«.

Обратите внимание, что пример сохранён 25.05.2017, в другой день все расчёты будут иными.

В строке 11 рассчитывается число купонов для погашения формулой «=ОКРУГЛВНИЗ(C7/365;0)*C10+1«: вычисляем количество полных лет до погашения, умножаем на количество купонов в год и добавляем 1 (так как последний купон выплачивается в момент погашения).

В строке 13 рассчитывается накопленный купонный доход (НКД) формулой «=(СЕГОДНЯ()-C12)/365*C9*C5«: он зависит от текущей даты, даты последней выплаты купона, купонной доходности и номинала.

С помощью рассчитанного НКД и цены, по которой облигация торгуется на рынке («чистой цены»), рассчитывается так называемая «грязная цена» — стоимость, которую необходимо заплатить за покупку облигации (без учёта брокерских комиссий). Это сумма инвестиций.

В строках 17-20 рассчитывается доход от инвестирования в облигацию ОФЗ, равный доходу от погашения облигации плюс купонный доход за всё время инвестирования.

В строке 22 рассчитана прибыль, равная разности дохода и сумме инвестиций. В строке 23 — она же в процентном виде. Видим, что за время инвестирования сумма инвестиций более чем удвоилась, но срок очень долгий (14 лет) и простая доходность к погашению составила всего лишь 7,35%.

Эту таблицу можно использовать для расчёта простой доходности к погашению любых облигаций, которые имеют фиксированный купон и не предусматривают амортизацию номинала. Для более сложных случаев стоит составить таблицу платежей и поступлений (финансовых потоков) и использовать функцию Excel ЧИСТВНДОХ, как это сделано в следующем примере расчёта эффективной доходности облигации ОФЗ, смотрите соответствующую статью Расчёт эффективной доходности облигации к погашению.

Скачать пример расчёта простой доходности облигации ОФЗ к погашению: doh_obl_prost

finexcel.ru

HELP? Как же все таки считать доходность субфедеральных облигаций?

Добрый день, Всем!

Помогите разобраться, как считается доходность субфедеральных облигаций на СмартЛабе, а именно «Доходность облигации к погашению при текущей рыночной цене».

 И так согласно таблице самая «жирная» на текущий момент является облигация «Мордовия03» с доходностью 10,4%

Как считаю я:

Беру информацию с сайта RUSBONDS.

Анкета выпуска: Мордовия Респ-34003-об (в обращении)

Общие сведения:

Дата погашения:       03.09.2021

Размер купона, % годовых:  11,7

НКД:   19,23 RUB – как видим НКД не совпадает.

Мой расчет НКД:

= (Сегодня – Дата последнего выплаченного купона) / 365 * размер купона * номинал

= (06.02.2019 – 07.12.2018) / 365 * 11,7% *1000 = 19,55

Учитывая, что я живу во Владивостоке, корректирую на один день.

= (Сегодня – 1 день – Дата последнего выплаченного купона) / 365 * размер купона * номинал

= (05.02.2019  – 07.12.2018) / 365 * 11,7% *1000 = 19,23

Все как на сайте RUSBONDS.

У Тимофея 18,91 почему-то?

Предположу, что режим Т2, а смысл?

Поехали дальше.

Расчет доходности:

Считаю купонный доход:

= 3 * 29,17 + 4 * 20,42 + 4 * 11,67 = 215,87

Годовая доходность:

Начало: 06.02.2019

Конец: 03.09.2021

Срок: 940 дней или 2,6 года

Годовая доходность: = 16,5% / 940 * 365 = 6,4%

 Делаю пересчет с учетов амортизации:

Получаю годовая доходность с учетом амортизации: = 16,5% / 612 * 365 = 9,8%

На Смар Лабе 10,4%.

Предположу (хотя могу ошибаться, просто цифры совпали), что Тимофей в расчете купонного дохода считает 11 выплат * 29,17 = 320,87

тогда доходность облигации 26,5%, а годовая 26,5/940*365 = 10,3% что очень близко к цифрам на сайте, там 10,4%, но при этом не учитывается амортизация. Хотя это может быть просто совпадение цифр.

Соответственно вопрос, так как-же все таки считать правильно доходность субфедеральных облигаций?

HELP?

smart-lab.ru