Формулы фишера: ХиМиК.ru — ФИШЕРА ФОРМУЛЫ — Химическая энциклопедия

Фишера формулы формил — Справочник химика 21

    Сахара содержат несколько хиральных центров, и различным диастереомерам даны разные названия. Так, глюкоза, манноза и галактоза— это попросту три из восьми возможных диастереомерных альдо-гексоз (другими являются аллоза, альтроза, гулоза, идоза и талоза) [6]. Каждый из этих сахаров представлен парой форм (энантиоме-ров)—О и Ь, являющихся зеркальным отображением одна другой. Для иллюстрации взаимоотношений между сахарами часто пользуются проекционными формулами Фишера (разд. А.4), как это показано на рис. 2-13. Проекционные формулы удобны для сопоставления структур сахаров, но они дают весьма смутное представление о их трехмерной структуре. Согласно указанию Фишера, вертикальные связи при каждом атоме углерода следует представлять уходящими за данный атом. В действительности молекула такую конформацию иметь не может. Сравните, например, трехмерную структуру рибита (разд. А.6), образующегося при восстановлении глюкозы, с его формулой Фишера.  [c.108]

    Фишера формула — открытая форма моносахарида (глюкозы). [c.497]

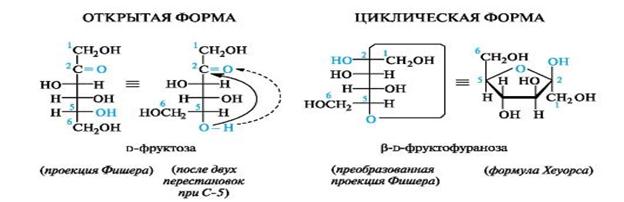
    Результаты анализов указывают на то, что данное вещество — Д-фруктоза, составная часть тростникового сахара. Ее пространственное строение в открытой (нециклической) форме можно изобразить с помощью проекционной формулы по Фишеру. [c.175]

    Правила ШРАС по номенклатуре углеводов выработаны для того, чтобы, во-первых, дать название родоначальному моносахариду в ациклической форме, представленной проекцией Фишера, затем назвать циклическую форму и производные. Тщательно изучите прежде всего ациклические формы. Поскольку все углеводы имеют по крайней мере один хиральный центр, совершенно необходимо правильно использовать проекционные формулы Фишера. [c.231]

    Перспективные формулы Хеуорса Недостатки проекционных формул Фишера очевидны и связаны, во-первых, с неестественным изображением связи, образуемой атомом кислорода в цикле, во-вторых, с далеким от наглядности и действительной геометрии изображением циклической формы моносахаридов Хеуорс предложил изображать циклические формы моносахаридов в виде плоских шести- и пятичленных колец 

[c. 760]

    Взаимосвязь проекционных формул Фишера открытых цепей сахаров и формул Хеуорса кольцевых форм сахаров показана ниже на примере о-глюкозы и ее пиранозной кольцевой формы. [c.123]

    Более целесообразной формой записи проекционных формул Фишера представляются формулы (116) и в особенности (Ив). Их преимущество, во-первых, в том, что они наглядно изображают ту ориентацию заместителей относительно плоскости чертежа, о которой речь была в предыдущем абзаце. Во-вторых, именно условная (без изображения самих асимметрических атомов) форма записи (Ив) наглядно свидетельствует 

[c.155]

    Циклические формы моносахаридов принято изображать в перспективных формулах, предложенных У. Хеуорсом. Например, пиранозная форма О-глюкозы в формулах Э. Фишера и У. Хеуорса. [c.449]

    Конформации моносахаридов Формулы Хеуорса, несмотря на преимущества по сравнению с формулами Фишера, все-таки не отражают истинного пространственного строения циклических форм моносахаридов Если пятичленный цикл близок к плоской форме и формулы Хеуорса достаточно удовлетворительно описывают строение фураноз, то пиранозы имеют в основном конформацию кресло  [c.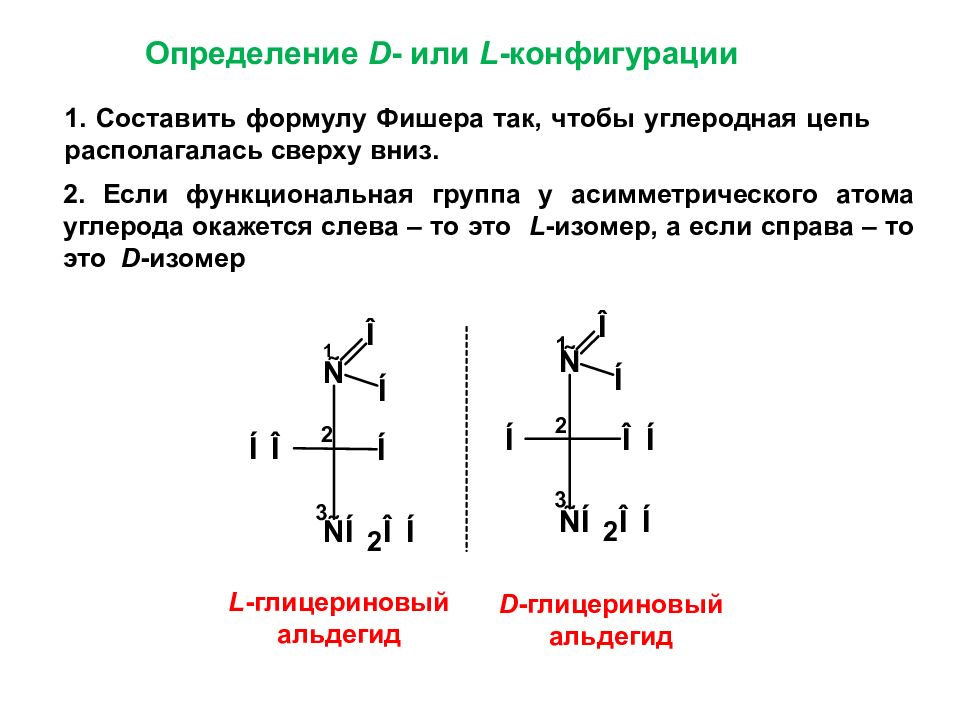 762]

    От названий эритрозы и треозы произошли терминологические приставки эритро-ч трео-, употребляющиеся для обозначения относительного расположения одинаковых (или родственных) заместителей у двух хи()альных атомов углерода. Если в проекционной формуле Фишера эти заместители находятся по одну сторону углеродной цепи, то такой стереоизомер называют эритро-формой, если по разные — то трео-формой. 

[c.78]

    Циклические таутомерные формы этих трех сахаров изображены ниже в проекциях Фишера и в перспективных формулах Хеуорса (в этих формулах плоскость шестичленного цикла следует рассматривать как лежащую перпендикулярно плоскости рисунка). Асимметрические атомы углерода в формулах Хеуорса, как и в проекциях Фишера, не указываются. [c.451]

    Эти противоречия открытым формулам Фишера можно объяснить, если принять, что истинное строение моносахаридов не отражается открытыми формулами и они являются таутомерными смесями открытой и циклической форм с преобладанием последних Так, в растворе глюкозы содержится около 0,024% открытой, альдегидной формы, в растворе рибозы — 8,5% альдегидной формы Кетозы содержат открытую форму в большей степени, чем альдозы Впервые предположение о внутримолекулярном присоединении гидроксильной группы по карбонильной группе глюкозы с образованием трехчленного этиленоксидного цикла сделал в 1870 году А Колли, позже Б Толленс (1883) предложил формулу с пятичленным кольцом, но только У Хеуорс в 1925-1930 годах экспериментально определил размер цикла для некоторых моносахаридов Хеуорс предложил называть моносахариды с пятичленным циклом фу- 

[c. 758]

    Хеуорс пересмотрел также способ написания формул моносахаридов. Формулы Э. Фишера при всех их достоинствах плохо отражают реальную форму молекул моносахаридов и громоздки. Хеуорс предложил свои так называемые перспективные формулы. Согласно его предложению, циклическую молекулу моносахарида условно считают плоской. Для изображения на бумаге ее мысленно располагают таким образом, чтобы кислородный атом пиранозного кольца находился на наибольшем расстоянии от глаза наблюдателя справа (у фуранозного кольца — посередине), а углеродная цепь была бы обращена выпуклой стороной к наблюдателю. Затем расположенную таким образом молекулу изображают по законам перспективы, как это представлено ниже, причем обычно часть молекулы, приближенную к наблюдателю, показывают жирной линией. 

[c.29]

    Для рассмотрения относительных и абсолютных конфигураций удобны формулы Фишера, но они сознательно игнорируют реальную форму молекулы формулы Ньюмена мало наглядны для суждения о конфигурации того или иного атома, но удобны в тех случаях, когда нужно продемонстрировать реальное положение тех или иных групп в пространстве, т.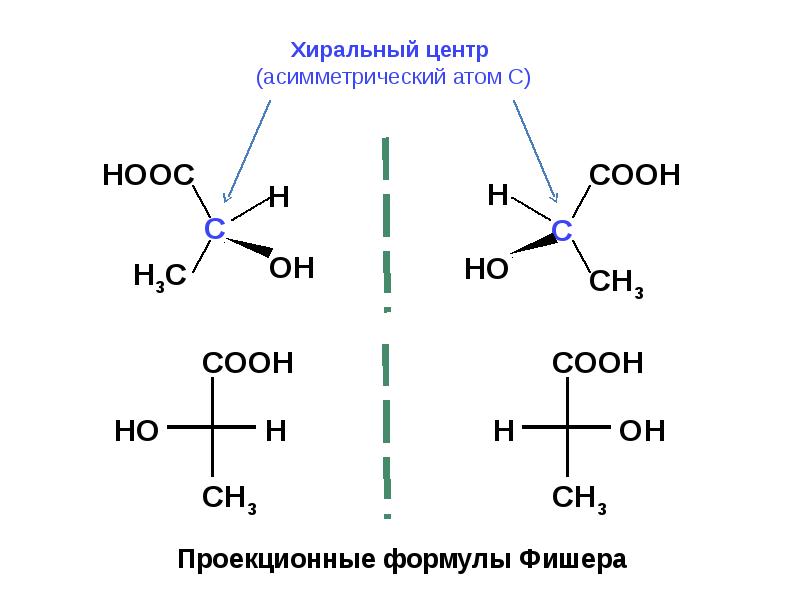 е. конформацию. [c.36]

    Открытая форма Формула Фишера [c.761]

    Это противоречие впервые объяснил Э Фишер, который, используя стереохимические представления Вант-Гоффа, определил относительные конфигурации ряда моносахаридов (глюкозы, фруктозы, маннозы, арабинозы) Графическое изображение пространственных конфигураций моносахаридов в открытой форме, например, методом проекции формул Э Фишера, имеет следующий вид [c.754]

    Формулы Фишера не отражают точно пространственное расположение молекулы в циклической форме. Например, в случае цикли- [c.106]

    При написании открытых форм кетоз пользуются проекционными формулами Фишера. Для циклических форм применяют формулы Хеуорса  [c.468]

    Вернемся к глюкозе, отвлекшись от проекционных формул Фишера и Хеуорса, и проанализируем ее пространственную структуру, так сказать, в окончательном варианте. Поскольку все шестичленные циклы, включая гетеро-атомные, предпочтительно существуют в форме кресла, так же изобразим и глюкозу.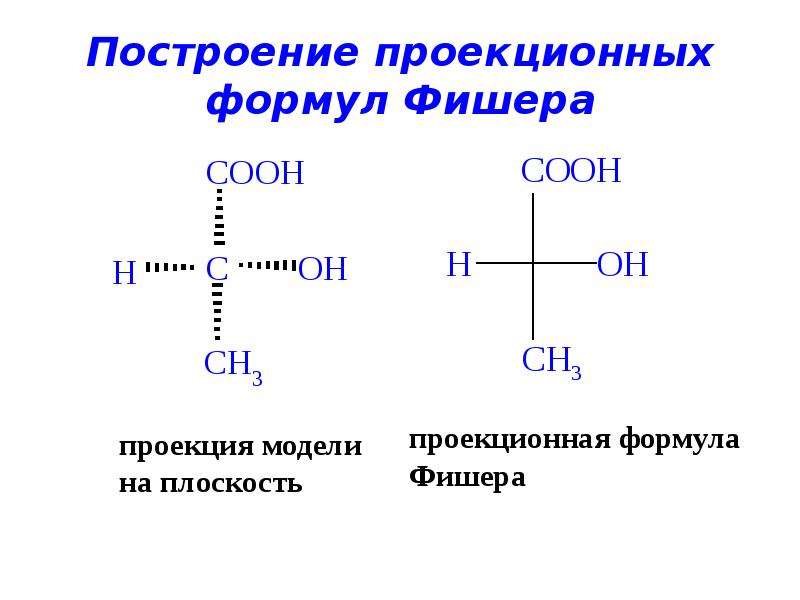

В таком случае, р-глюкопира-ноза окажется термодинамически предпочтительной и по стереохимичес-кому расположению всех заместителей цикла —они расположены экваториально. В связи с этим, становится понятным предпочтение, отданное Природой р-форме глюкозы при построении различных биологических структур, которые, [c.36]

    Открытые (незамкнутые) формы моносахаридов изображают в виде проекционных формул Фишера (см. 3.2.4). Углеродная цепь в них записывается вертикально. У альдоз наверху поме-щак т альдегидную группу, у кетоз — соседнюю с карбонильной первичноспиртовую группу. С этих групп начинают нумерацию цепи (табл. 12.1). [c.380]

    Формулы, а. Классические проекционные формулы Э. Фишера, которыми пользовались на предыдущих страницах, обладают тем преимуществом, что они очень наглядны и просты. Однако они довольно далеки от реальной формы молекулы. 

[c.214]

    Углеродные атомы в соединении I, помеченные звездочкой, асимметричны, и возможно, таким образом, существование 2, т. е. 16 оптически активных форм. Все они известны некоторые встречаются в природе, а другие были получены синтетическим путем. Проблема определения строения глюкозы как одного из шестнадцати возможных изомеров была разрешена Э. Фишером в конце XIX века. Конфигурации, установленные им для каждого из асимметрических атомов углерода от Сг до Сд показаны в проекционной формуле II [c.546]

    Количество диастереоизомерных моносахаридов. Если исходить из формул Фишера, то для альдогексоз должно существовать 16 диастереоизомеров. Действительно, это количество альдоз было найдено в природе или синтетически получено Фишером. Однако дальнейшие исследования показали, что каждый нз этих моносахаридов способен существовать в двух совершенно индивидуальных кристаллических формах с различными константами, в том числе с резко различными углами вращения. Так, например, были получены две О-глюкозы с углами вращения +106° и +22,5 . Характерно, что при растворении обеих форм моносахарида всегда получался раствор, угол вращения которого менялся вследствие мутаротации и постепенно достигал для обеих форм одной и той же всегда строго постоянной величины, которая для глюкозы составляла +52,5°.

Таким образом, число реально существующих альдоз ровно вдвое превышало число предсказанных на основе законов стереохимии. Удвоение числа диастереоизомерных форм говорило [c.224]

    Проекции Фишера очень удобны для установления связи между структурой и названиями моносахаридов и их производных однако они не дают представления о действительной форме колец Для этих целей получили распространение формулы Хеворта В них углеродная цепь изображается горизонтальной, потен циальная карбонильная группа должна находиться справа Углеродная цепь как бы находится перед плоскостью бумаги кислородный мостик — за ней. 

[c.238]

    Проекционные формулы Фишера не дают наглядного представления о пространственном строении полуцетальных форм, поэтому циклические структуры удобнее изображать с помощью проекционных формул Хеуорса (в приводимых далее формулах атомы Н не указаны, чтобы не загромождать рисунок)  [c.78]

    Для изображения циклических форм могут применяться и проекционные формулы Э.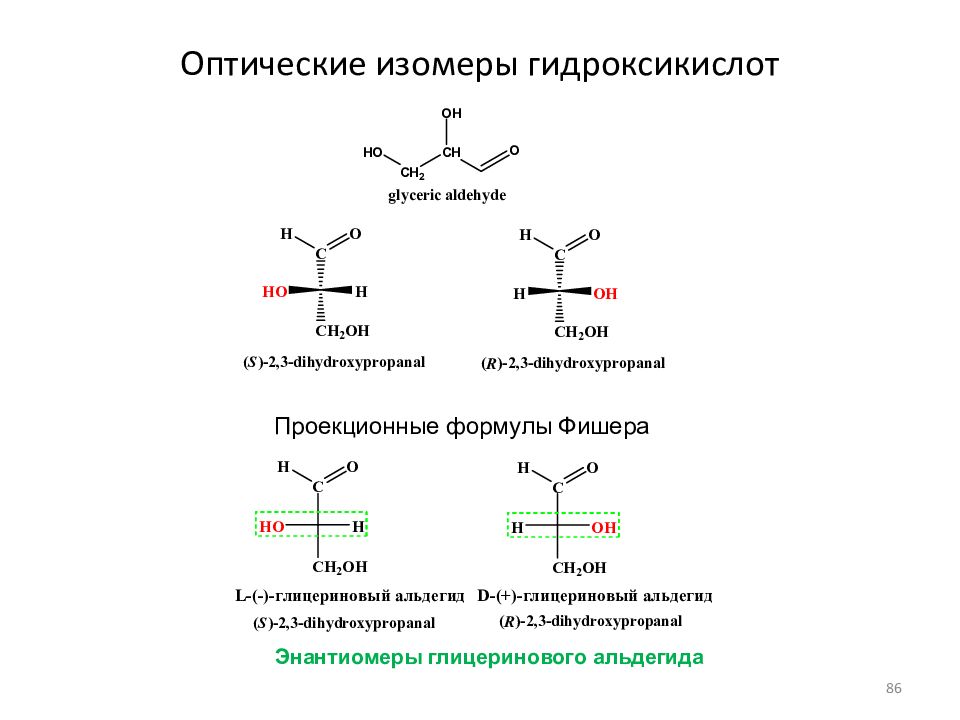 Фишера, но это не дает наглядной картины. Лучше всего пользоваться перспективными формулами У. Хеуорса (W. Haworth, 1929), как плоскими, так н изогнутыми. Ниже приведены все три способа изображения для a-D-глюкоииранозы  [c.509]

    Э. Фишер подробно изучил строение и свойства глюкозы, в том числе стереохимию этого моносахарида. Он установил, что значительная часть свойств глюкозы может быть понята в терминах открытой формы. Вместе с тем следует иметь в виду возможность перехода открытой формы формула Фишера) в циклическую форму формула Толленса). Шестичленные циклические формы моносахаридов называют пиранозами (в основе этого термина лежит название оксациклогексадиенов — пиранов). [c.475]

    В циклических формах моноз на один асимметрически атом углерода больше, чем в открытых, поэтому у них в два р за большее число оптических изомеров (за счет а- и Р-форм что объясняет несоответствие между количеством реально сз ществующих изомеров и предсказанных по формуле Фишера.  [c.462]

    Способы изображения циклических форм моносаха-идов Графическое изображение циклических форм вызы-ает определенные трудности Самый простой способу с по-ющью проекционных формул Фишера, предполагает тран-формацию проекционной формулы открытой формы мо-озы в циклическую и применение изогнутой линии для зображения химических связей, образуемых атомом кис-орода, входящим в цикл [c.759]

    Капиллярная конденсация описывается обычно уравнениями Томсона, применимыми для круглых цилиндрических капилляров. В действительности, структура пор адсорбентов весьма сложна и не отвечает представлению о таких капиллярах. Кистлер, Фишер и Фримен в 1943 г. сделали важную попытку обобщить представления о капиллярной конденсации паров на поры любой формы при помощи уравнения Больцмана и получили формулу для определения поверхности адсорбционной пленки на которой начинается капиллярная конденсация. [c.186]

    Углеродные атомы 2 и 4 — это обычные центры асимметрии, но углерод 3 ваг5ывается псевдоасимметрическим, так как его сво11ства симметрии зависят от конфигурации вокруг атомов 2 и 4.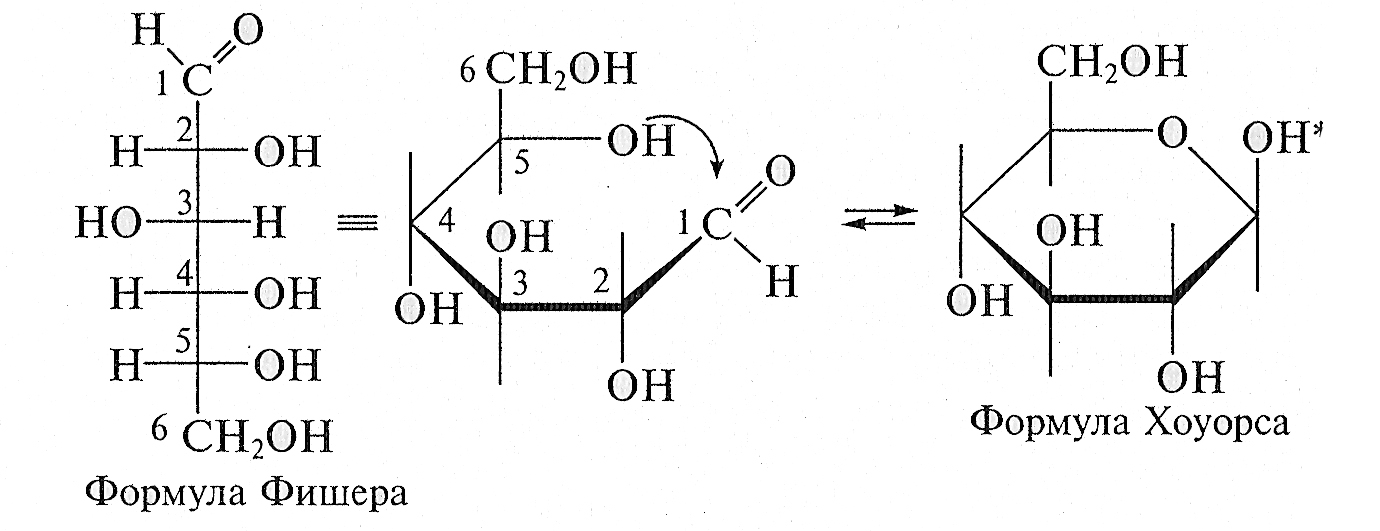 Можно написать четыре стереомер-ные конфигурации, обладающие структурой XXV. Две из них — симметричные, или лез , формы, которые имеют зеркальные плоскости, проходящие через углерод 3 и связанные с ним водород и гидроксил. Два других стереоизомера энантиоморфны и в смеси образуют рацемат. Эти соотношения представлены на следующих проекционных формулах Фишера  [c.141]

    Указания на существование фуранозиых форм в растворах моносахаридов были получены, например, в случае образования метилглюкозидов D-глюкозы, при обработке метанолом и хлористым водородом. Если эта реакция проводится при комнатной температуре, то наряду с кристаллическими а- и р-метил-О-глюко-пиранозидами, о которых сказано выпю, образуется также в меньшем количестве изомерный жидкий метилглюкозид, названный открывшим его Э. Фишером (1914 г.) у-метилглюкозидом. Это соединение перегоняется в вакууме без разложения и отличается чрезвычайной легкостью, с которой оно гидролизуется даже очень слабыми кислотами, регенерируя D-глюкозу и метанол. Методом метилирования было доказано, что это соединение представляет в действительности смесь а- и р-метил-D-глюкофуранозидов, соответствующих приведенной выше формуле. [c.214]

    Имеет значение то, что все четыре пиррольных ядра порфина эквивалентны, причем место атомов водорода неопределенно. Если бы атомы водорода были локализованы при определенных атомах азота, то однозамещенные производные порфина должны были бы возникать в изомерных формах, которые не были обнаружены в действительности (та же проблема, что и в случае бензола). Порфиновое кольцо изображается, как правило, формулой 1а (по В. Кюстеру и Г. Фишеру), имеющей то же значение, что только одна из двух формул Кекуле для бензола [c.622]

---

Пространственные формулы Фишера — Справочник химика 21

    Конфигурацию протеиногенных аминокислот соотносят с о-глюкозой такой подход предложен Э. Фишером в 1891 г. В пространственных формулах Фишера заместители у хирального С-2 атома занимают положение, которое соответствует их абсолютной конфигурации (это было доказано через 60 лет).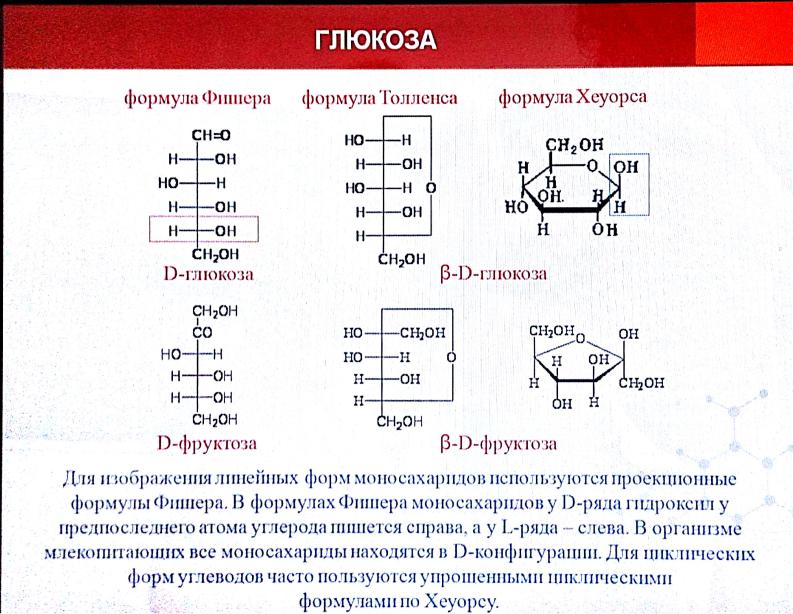  [c.26]

    ПРОСТРАНСТВЕННЫЕ ФОРМУЛЫ ФИШЕРА [c.308]

    Существование пары оптических антиподов — проявление пространственной изомерии (стереоизомерии) молочной кислоты. С помощью проекционных формул Фишера строение оптических антиподов молочной кислоты изображается так  [c.263]

    Используя пространственную формулу правовращающей глюкозы в качестве опорной точки и обозначив пространственную конфигурацию, присущую этому веществу, знаком с1, Э. Фишер предложил относить к -ряду все соединения, которые можно получить из правовращающей глюкозы, например  [c.296]

    Фишеровские проекции. Для того чтобы выяснить отношения между относительной и абсолютной конфигурацией, необходимо сначала ознакомиться с изображением на плоскости (в двух измерениях) стереохимических формул, которые имеют пространственный смысл (три измерения). Приводим два способа изображения.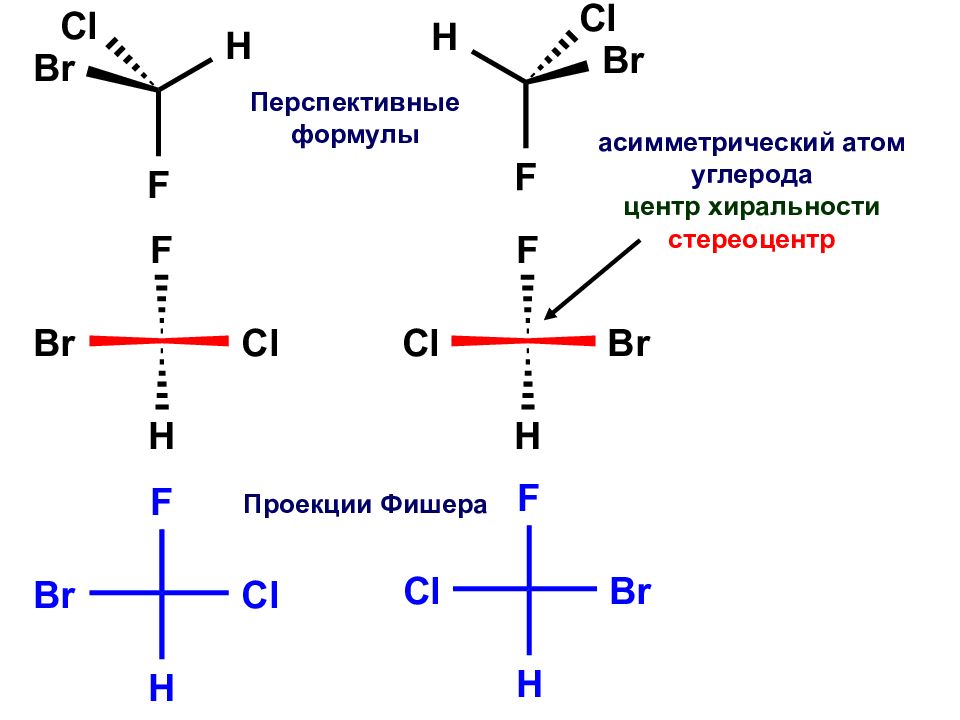 Слева (формула а и 16) — это, по существу, перспективный рисунок, который мало применим для случаев с многими асимметрическими атомами, справа — проекционные формулы Фишера (Па и б)  [c.383]

    Поскольку на тетраэдр можно смотреть с разных сторон, одна модель может дать 12 внешне непохожих формул Фишера. Чтобы получить правильные результаты, необходимо помнить, что формулы Фишера являются проекциями на плоскость, и их нужно рассматривать иначе, чем пространственные модели. Поэтому вводится ряд ограничений. Формулу нельзя выводить из плоскости чертежа и нельзя поворачивать на 90 , хотя поворот на 180° допустим  [c.36]

    Имея в виду пространственную ориентацию вертикальных и горизонтальных линий связей в проекционной формуле Фишера, с этой формулой можно обращаться как с тетраэдрической моделью и определять по ней тин энантиомера в / ,5-номенклатуре. Существует и более формализованная процедура определения абсолютной конфигурации по формуле Фишера.  [c.191]

    Конформации моносахаридов Формулы Хеуорса, несмотря на преимущества по сравнению с формулами Фишера, все-таки не отражают истинного пространственного строения циклических форм моносахаридов Если пятичленный цикл близок к плоской форме и формулы Хеуорса достаточно удовлетворительно описывают строение фураноз, то пиранозы имеют в основном конформацию кресло  [c.762]

    Формулы Фишера не отражают точно пространственное расположение молекулы в циклической форме. Например, в случае цикли- [c.106]

    Циклические формулы в том написании, которым мы пользовались до сих пор проекционные формулы Фишера), недостаточно наглядно передают пространственное строение молекулы. Гораздо нагляднее иной способ написания с нормальным обозначением пяти- или шестичленного кольца. [c.371]

    Обозначения D- я L- в названиях гидроксикислот указывают условно НХ конфигурацию, т. е. пространственное расположение заместителей вокруг асимметрического атома углерода. Обозначение D- получают те гидроксикислоты, у которых гидроксильная группа в проекционной формуле Фишера стоит справа обозначение L-ставится, если гидроксильная группа в проекционной формуле оказывается слева. [c.323]

    Формула Фишера Формула Хеуорса В циклических формах моносахаридов появляется еще один асимметрический атом углерода (С-1 у альдоз и С-2 у кетоз). Этот асимметрический атом углерода называется аномерным. Изомеры углеводов, отличающиеся расположением атомов и атомных групп у аномерного атома углерода, называются аномерами. Стереоизомер (пространственный изомер), в котором группа —ОН у аномерного атома С располагается под плоскостью цикла, называется а-аномером, а стереоизомер с противоположным расположением ОН-группы называется Р-аномером  [c.664]

    Для изображения на бумаге конфигурации таких молекул в настоящее время применяют предложенные Фишером так называемые проекционные формулы, Для этого связанные в цепи углеродные тетраэдры представляют в виде развернутой прямой линии, приче. м все имеющиеся группы располагаются над плоскостью бумаги атомные группы, связанные с углеродными атомами, при этом оказываются вправо и влево от прямой, на которой находятся углеродные ато.мы. Проекция всех групп па бумагу позволяет представить их взаимное пространственное расположение. [c.140]

    Пространственное строение оптических антиподов мы выражали до сих пор лишь с помощью рисунков или проекционных формул по Фишеру, однако еще не научились давать им названия. Между тем формулы можно употреблять далеко не всегда — их нельзя применять в устной речи, нельзя включить в алфавитном порядке в словари, справочники. Любой предмет, в том числе и оптический антипод, должен иметь свое название в данном случае название должно отражать особенности пространственного строения молекул. [c.64]

    Результаты анализов указывают на то, что данное вещество — Д-фруктоза, составная часть тростникового сахара. Ее пространственное строение в открытой (нециклической) форме можно изобразить с помощью проекционной формулы по Фишеру.  [c.175]

    Фишера формулы (проекции Фишера) — способ изображения на плоскости пространственных структур молекул, имеющих хиральные центры. Проекции Фишера применимы для соединений с несколькими хи-ральными центрами, в том числе и дпя молекул, изображение которых в трехмерном пространстве затруднено. [c.324]

    Э. Фишер предложил следующий способ изображения пространственного строения оптических изомеров молекул на плоскости. Для написания проекционной формулы тетраэдрическую модель молекулы (рис. 79, а) располагают так, чтобы рассматриваемый асимметрический атом углерода лежал в плоскости чертежа, связи С —Ь и С —с лежали в горизонтальной плоскости, выступая на нас из плоскости чертежа. При этом связи С —а и С —(1 располагаются в вертикальной плоскости, уходя за плоскость чертежа (рис. 79, б). Видимую в таком положении картину проецируют на вертикальную плоскость (рис. 79, в). Схема обратного перехода от фишеровских формул к тетраэдрической модели заключается в том, что связи, образуемые асимметрическим атомом с группами Ь и с (находящимися в горизонтальной плоскости), считаются направленными вперед, выступают из плоскости бумаги, а связи с группами а и (1 (находящимися в вертикальной плоскости) как бы уходят за плоскость бумаги.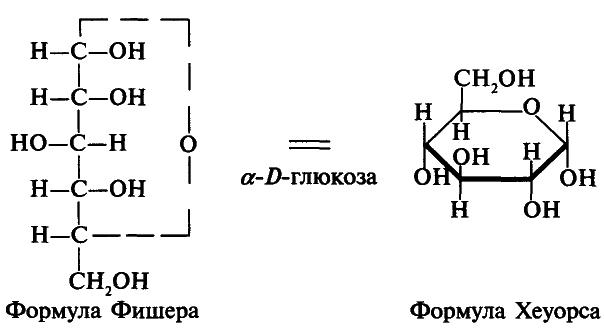 Проекционные формулы, отвечающие одному из оптических изомеров, нельзя выводить из плоскости чертежа, поворачивать в плоскости на 90 и 270° и [c.436]

    Для более быстрого и удобного написания конфигурации моноз Э. Фишер предложил изображать их проекционными формулами. Углеродная цепь изображается вертикальной линией, на концах которой пишут первую и последнюю функциональные группы (альдегидную группу всегда пишут вверху). Группы Н и ОН пишут справа или слева от цепи, в соответствии с их пространственным расположением в молекуле. Например, глюкоза, по Фишеру, пишется так  [c.456]

    Это противоречие впервые объяснил Э Фишер, который, используя стереохимические представления Вант-Гоффа, определил относительные конфигурации ряда моносахаридов (глюкозы, фруктозы, маннозы, арабинозы) Графическое изображение пространственных конфигураций моносахаридов в открытой форме, например, методом проекции формул Э Фишера, имеет следующий вид [c.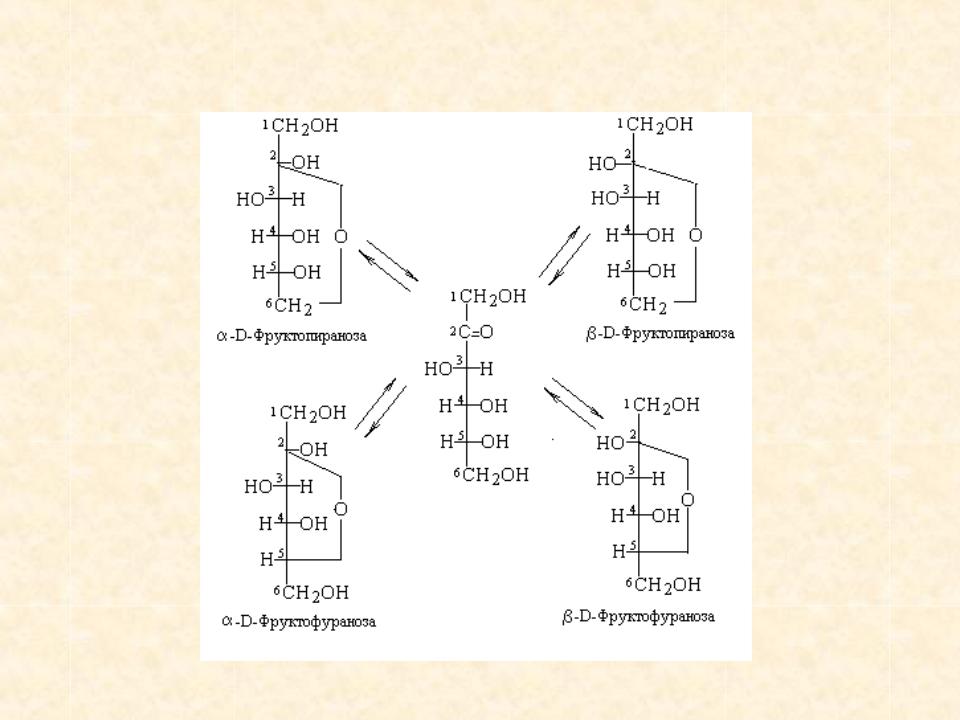 754]

    Все стереохимические формулы в Приложении даются либо в виде проекций Фишера, повернутых на 90°, либо в виде гипотетического выпрямленного зигзага. Второй вариант отображения иногда дает более ясное представление о пространственной структуре. Предпочтительно, чтобы гипотетические вытянутые зигзагообразные цепи были изображены в виде сплошной линии со связью в основной цепи крайней слева от формулы и идущей слева направо и пунктиром была обозначена связь от любого атома углерода в основной цепи влево от сплошной линии. [c.550]

    Пространственные конфигурации моносахаридов D- и L-ряды. Моносахариды содержат асимметрические углеродные атомы тетрозы — два асимметрических углеродных атома, пентозы — три, гексозы — четыре. Благодаря этому у моносахаридов мы встречаем большое число стереоизомеров, которые удобно изображать, пользуясь проекционными формулами Э. Фишера (см. стр. 577 сл.). Упрощенное проекционное [c.625]

    Для изображения пространственных антиподов приняты проекционные формулы Фишера. Д/[я этого выбирается главная цепь молекулы НСНХЙ так, чтобы наверху оказалась. самая старшая группа (старшинство учитывается по женевской номенклатуре, в частности, СООН > СНО > СН2ОН > СНд). Все тетраэдры располагаются так, чтобы их горизонтальные ребра лежали впереди вертикальных, как бы выступая из плоскости чертежа. Если при этом заместитель X окажется по правую сторону чертежа, то такая конфигурация обозначается правой О. [c.105]

    Вернемся к глюкозе, отвлекшись от проекционных формул Фишера и Хеуорса, и проанализируем ее пространственную структуру, так сказать, в окончательном варианте. Поскольку все шестичленные циклы, включая гетеро-атомные, предпочтительно существуют в форме кресла, так же изобразим и глюкозу. В таком случае, р-глюкопира-ноза окажется термодинамически предпочтительной и по стереохимичес-кому расположению всех заместителей цикла —они расположены экваториально. В связи с этим, становится понятным предпочтение, отданное Природой р-форме глюкозы при построении различных биологических структур, которые, [c. 36]

    С 1861 г., т. е. с момента опубликования А. М. Бутлеровым статьи О химическом строении тел , начались непрерывные поиски изображения структурных формул молекул. Оказалось, что для изображения молекул алканов, алкенов, алкинов, алленов не существует проблем. Здесь достаточно эффективны классические формулы строения — плоскостные формулы Бутлерова, пространственные формулы Вант-Гоффа, конформащгонные проек-щш Ньюмена, зеркально-симметричные проекционные формулы Фишера для оптических изомеров. Перечисленные способы изображения геометрического и электронного строения молекул пригодны также для всех функциональных производных вышеперечисленных углеводородов, если только функциональные группы не дают сопряженных химических связей. [c.76]

    Изобразить на бумаге пространственную формулу сложного анического соединения довольно трудно. Поэтому в 1891 г. Фишер предложил представлять пространственное строение в оекций, названных его именем. [c. 35]

    Проекционные формулы Фишера не дают наглядного представления о пространственном строении полуцетальных форм, поэтому циклические структуры удобнее изображать с помощью проекционных формул Хеуорса (в приводимых далее формулах атомы Н не указаны, чтобы не загромождать рисунок)  [c.78]

    Винные кислоты НООССН(ОН)СН(ОН)СООН — бесцветные, растворимые в воде кристаллические вещества с приятным кислым вкусом. Молекулы их содержат два асимметрических углеродных атома с одинаковым набором заместителей известны два оптически активных изомера (+) и (—), оптически неактпвная рацемическая ( )-винная кнслота и оптическая неактивная мезовинная кислота, которую невозможно расщепить на оптические антиподы (см. гл. VII. 3.3). Ниже изображено пространственное строение винных кислот при помощи формул Фишера, клиновидных проекции и формул Ньюмена. Клиновидные проекции изображают два кон( юрме-ра, один из которых соответствует ф ормуле Фишера. Для обозначения стереоизомеров применена / ,5-система  [c.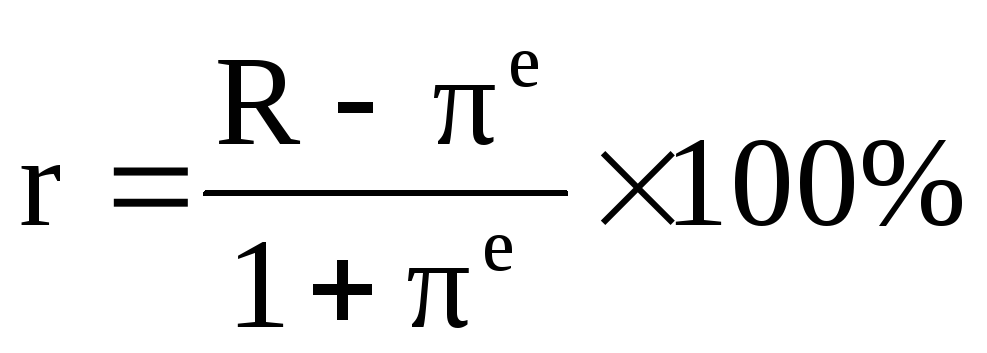 613]

    Так вот, если в прохиральном глицерине верхнюю группу (в приведенной формуле Фишера) пометить ( С, например, или С), то в реакции принимает участие всегда нижняя группа. Изобразив пространственную структуру глицерина и фрагмент участка фермента, в котором точка 3 соответствует прикреплению грзшпы СН2ОН, точка 2 — группы Н и точка [c.568]

    Выше два энантиомера в/пор-бутилового спирта (II и III) изображали с номош ью пространственных моделей, стремясь при этом показать тетраэдрическое расположение групп при асимметрическом углеродном атоме. Очевидно, что это неудобно, особенно для более сложных примеров. Необходимо поэтому располагать простым способом изображения, отражаюш им различие между оптическими изомерами. Для этой цели широко используются так называемые проекционные формулы Фишера с их помош ью энантиомеры епгор-бутилового спирта изображаются так, как это представлено формулами IV и V. [c.510]

    Когда в 1914 г.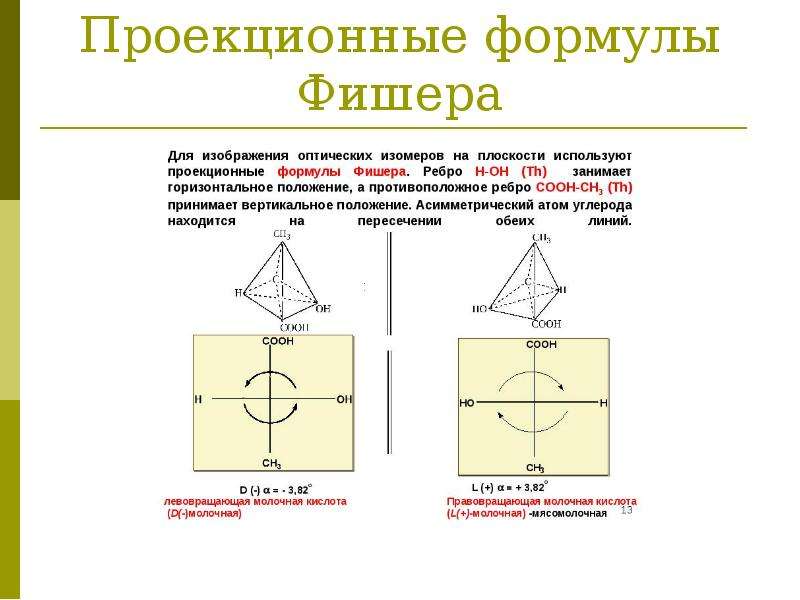 был впервые получен оптически активный ]лицериновый альдегид, появилась возможность экспериментально, а не только умозрительно установить конфигурации по этому простейшему оптически активному моносахариду. Для этого было необходимо выяснить связь глицеринового альдегида с конфигуративной системой сахаров и оксикислот, созданной на основе постулата Фишера о пространственной формуле правовраш,аюш,ей глюкозы. Эту задачу выполнили в 1917 г. Воль и Момбер , проведя синтез винной кислоты из глицеринового альдегида  [c.225]

    При прпведенныл схемах можно пользоваться упрощенной транскрипцией пространственных формул, введенной Э. Фишером, которая и в дальнейше.м окажет нам много услуг. Рис. 47 и 48 дают пространственное представление о двух связанных между собой углеродных атомах С ab  [c.220]

    После создания оксикарбонильных формул Э. Фишером (который одновременно разработал и дошедшую до наших дней номенклатуру сахаров) стало яспо, что для получения определенного сахара надо не только создать углеродную цепь соответствующей длины и не только присоединить к каждому углероду гидр-оксогрунпу, но и предусмотреть ее пространственное положение.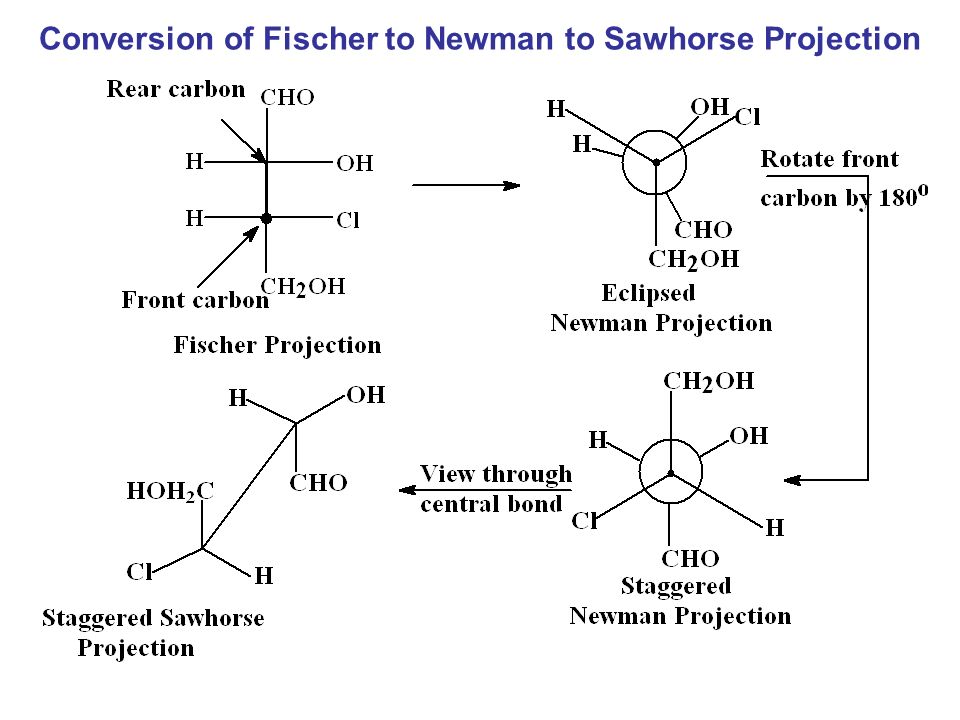 Возникла проблема стереоспецифического синтеза. [c.258]

    Заслуга точного установления структуры сахаров принадлежит Э, Фишеру, установившему строение и пространственное расположение атомов в молекулах простых сахаров — гексоз и пентоз. До работ Э. Фишера было известно несколько природных моносахаридов (гексоз), имеющих общую формулу СбН120в. Важнейшими из них являются глюкоза, фруктоза, галактоза и сорбоза. Изучение их состава обнаружило, что они содержат в молекуле по пять гидроксогр п и представляют собой либо альдегиды (глюкоза), либо кетоны (фруктоза). Г. Килиани (1855—1945), работавший в Мюнхене, а затем во Фрейбур-ге, пришел к выводу, что эти моносахариды представляют [c.182]

---

Проекционные формулы Фишера

Для изображения на iплоскости молекул с асимметрическими атомами углерода часто используют проекции, предложенные в 18Э1 году Э. Фишером.

Рассмотрим принцип их построения на примере молекулы бромфторхлорметана. Исходным пунктом при построении проекций Фишеоа служит^{пространственная модель молекулы или ее клиновидная проекция.
Расположим молекулу таким образом, чтооы в плоскости чертежа остался только атом углерода молекулы бромфторхлорметана, как это показано на рисунке:}

Спроектируем на плоскость чертежа все атомы (Вг и CL снизу вверх, так как они расположены под плоскостью чертежа, а F и H- сверху вниз). Для того, чтобы полученная проекция отличалась от структурной формулы, условимся не изображать асимметрический атом углерода. Он подразумевается в проекции Фишера на месте пересечения вертикальной и горизонтальной линий:

Как видно из приведенного примера, проекция Фишера строится таким образом, чтобы связи асимметрического атома с заместителями изображались вертикальными и горизонтальными (но не наклонными!) линиями.

При пользовании проекциями Фишера важно помнить, что вертикальная линия в них изображает связи, удаляющиеся от нас, а горизонтальная линия — связи, направленные к нам. Отсюда вытекают правила пользования проекциями Фишера:

НЕЛЬЗЯ:
1) Нельзя выводить проекцию из плоскости чертежа (например,просматривать ее «на просвет*, то есть с другойсторонылиста).
2) Нельзя поворачивать проекцию вплоскости чертежа на 90° и 270°.
3) Нельзя менять местами два любых заместителя при асимметрическом атоме.

МОЖНО:
1)Можно поворачивать проекцию в плоекостй чертежа на 180°. При таком повороте вертикальные линииостаются вертикальными, а горизонтальные — горизонтальными.
2)Можно производить четное число парных перестановок заместителей при асимметрическом атоме.
3) Можнопроизводить круговую перестановку трех заместителей при асимметрическом атоме. Четвертый заместитель при этом остается на своем месте.

N52

Асимметрический атом углерода связан с четырьмя неэквивалентными группами в молекуле глюкозы к числу таких атомов принадлежат атомы углерода с номерами от 1 до 5

Антиподы

вещество, характеризующееся противоположными по знаку и одинаковыми по величине вращениями плоскости поляризации света при идентичности всех других физических и химических свойств (за исключением реакций с другими оптически активными веществами и физических свойств в хиральной среде)

Рацемат — эквимолярная смесь двух энантиомеров(Энантиомеры (др. -греч. ἐνάντιος + μέρος — противоположный + часть, мера) — пара стереоизомеров, представляющих собой зеркальные отражения друг друга, не совмещаемые в пространстве). Рацематы не обладают оптической активностью, а также отличаются по свойствам от индивидуальных энантиомеров. Являются продуктами нестереоселективных реакций

Типы рецаматов

· Рацемический конгломерат представляет собой механическую смесь кристаллов двух энантиомеров соотношением 1:1, при этом каждый кристалл состоит из молекул только одного энантиомера.

· Рацемическое соединение (истинный рацемат) состоит из кристаллов, в каждом из которых находятся молекулы обоих энантиомеров и их соотношение равно 1:1. Такое соотношение энантиомеров в рацемических соединениях сохраняется до уровня кристаллической решётки.

· Псевдорацемат является твёрдым раствором двух энантиомерных соединений, то есть представляет собой гомогенную разупорядоченную смесь энантиомеров соотношением 1:1.

Физические свойства

· Оптическая активность. Рацематы не проявляют оптической активности, то есть не вращают плоскость поляризации света^[1]. Данное явление объясняется тем, что для энантиомеров оптическое вращение противоположно по знаку, но равно по величине. Поскольку вращение является аддитивной величиной, в случае рацемата из-за компенсации вкладов энантиомеров оно равняется нулю.

· Форма кристаллов. Поскольку энантиомеры образуют энантиоморфные кристаллы, рацемические конгломераты существуют в виде двух типов кристаллов, которые по форме являются зеркальными отражениями друг друга. Именно этот факт позволил Л. Пастеру вручную разделять кристаллы рацемических тартратов^[6].

· Плотность. Согласно правилу Валлаха, сформулированному в 1895 году, кристаллы рацематов имеют более высокую плотность, чем кристаллы индивидуальных энантиомеров. Это связывают как с термодинамическими факторами, так и с кинетикой нуклеации и роста кристаллов рацемического соединения.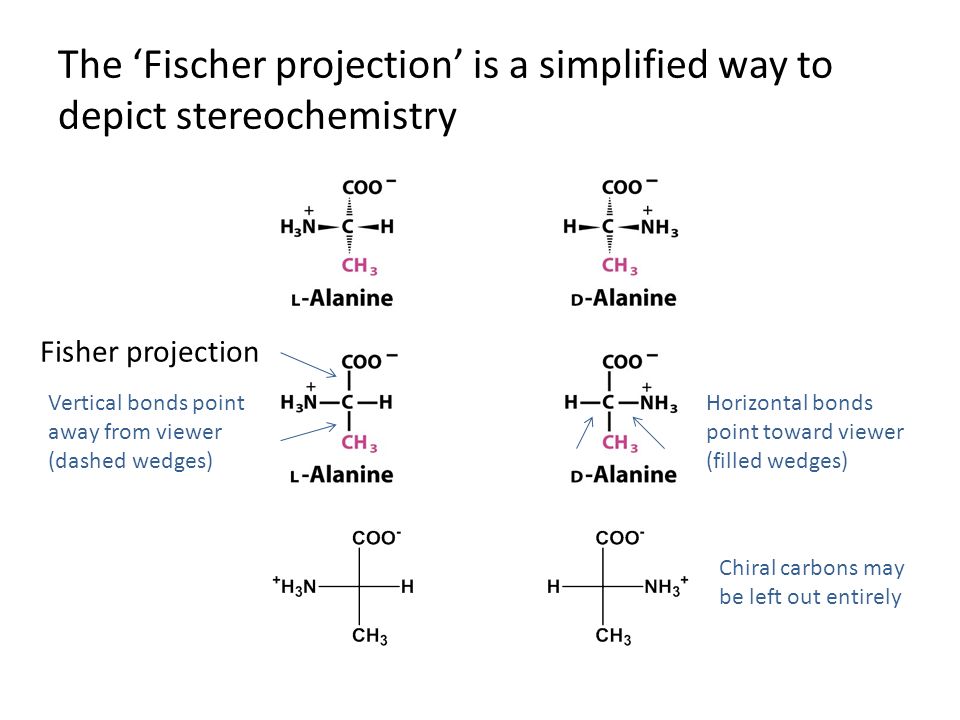 Данное правило было подтверждено анализом кристаллографической базы данных^[7].

· Температура плавления. Для рацемического конгломерата температура плавления всегда ниже температуры плавления индивидуальных энантиомеров, что видно по его диаграмме состояния. Например, энантиомерно чистый гексагелицен плавится при 265—267 °С, а рацемат — при 231—233 °С^[8].

Если рацемат является истинным, что характерно для большинства органических рацематов, то температура его плавления может быть как выше, так и ниже температуры плавления энантиомеров. Так, в случае диметилтартрата температуры плавления чистого энантиомера и рацемата равны соответственно 43,3 °С и 86,4 °С. Рацемат миндальной кислоты, напротив, плавится при более низкой температуре, чем энантиомерно чистое вещество (118,0 °С и 132,8 °С соответственно). Добавление индивидуального энантиомера к истинному рацемату всегда приводит к понижению температуры плавления, в отличие от того, что наблюдается для конгломератов^[9].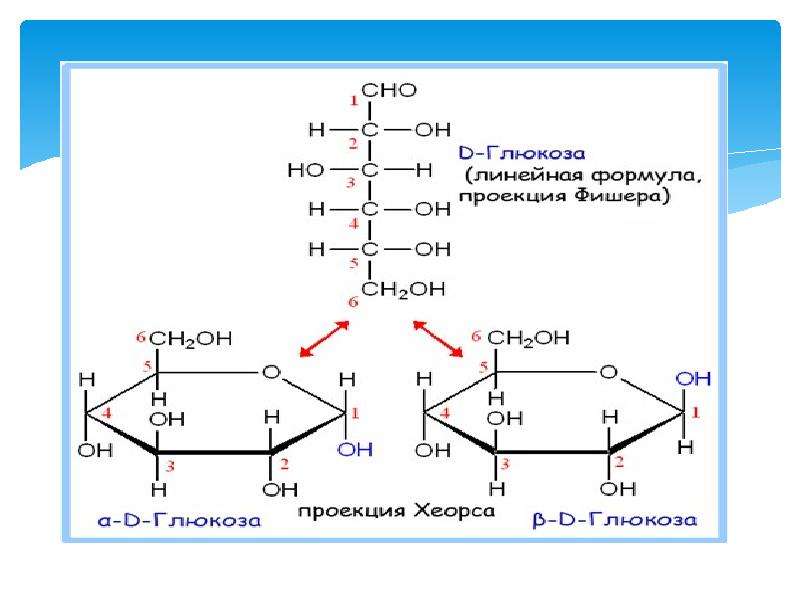

В редких случаях, когда рацематы проявляют свойства твёрдых растворов, они плавятся при той же температуре, что и индивидуальные энантиомеры (для камфоры — ≈178 °С)^[10].

· Растворимость. Для большинства хиральных соединений характерны различия в растворимости рацемата и индивидуальных энантиомеров. Растворимость рацемических конгломератов выше растворимости чистых энантиомеров. Эмпирическое правило Мейерхоффера, применимое к недиссоциирующим органическим соединениям, гласит, что растворимость рацемата вдвое больше растворимости энантиомеров. Для истинных рацематов растворимость может быть больше или меньше растворимости энантиомеров

N53

Реакции моносахаридов

 

N54

Глюко́за, или виноградный сахар, или декстроза (D-глюкоза), С₆H₁₂O₆ — встречается в соке многих фруктов и ягод, в том числе и винограда, от чего и произошло название этого вида сахара. Является моносахаридом и шестиатомным сахаром (гексозой). Глюкозное звено входит в состав полисахаридов (целлюлоза, крахмал, гликоген) и ряда дисахаридов (мальтозы, лактозы и сахарозы), которые, например, в пищеварительном тракте быстро расщепляются на глюкозу и фруктозу.

D-Фруктоза

Получают в виде β-формы. Очень гигроскопичные бесцветные призмы или иглы. tпл. 103-105 (разлагается).
Удельное оптическое вращение для D-линии натрия при температуре 20°С: [α]_D²⁰ -132,2 → -92,4 (с=4 в Н₂О).
Растворимость: 375²⁰, 740⁵⁵ в Н₂О; растворим в МеОН, ЕtОН, пиридине, ацетоне, ледяной уксусной кислоте.
Безводная форма устойчива при температуре > 21,4 °С. Способна гидратироваться с образованием полугидрата (и дигидрата) при температуре < 20°С. Перекристаллизовать из МеОН. Положительная реакция Селиванова. Кристаллический сахар — β-D-пираноза, но в растворе содержится ≥ 15% фуранозной формы и значительное количество открытой линейной формы. В составе соединений найдена только фуранозная форма. Сладкий вкус.

Аскорби́новая кислота́ (от др.-греч. ἀ — не- + лат. scorbutus — цинга) — органическое соединение с формулой C₆H₈O₆, является одним из основных веществ в человеческом рационе, которое необходимо для нормального функционирования соединительной и костной ткани. Выполняет биологические функции восстановителя и кофермента некоторых метаболических процессов, является антиоксидантом. Биологически активен только один из изомеров — L-аскорбиновая кислота, который называют витамином C. В природе аскорбиновая кислота содержится во многих фруктах и овощах^[3].

Гликози́ды — органические соединения, молекулы которых состоят из двух частей: углеводного (пиранозидного или фуранозидного) остатка и неуглеводного фрагмента (т. н. агликона). В качестве гликозидов в более общем смысле могут рассматриваться и углеводы, состоящие из двух или более моносахаридных остатков.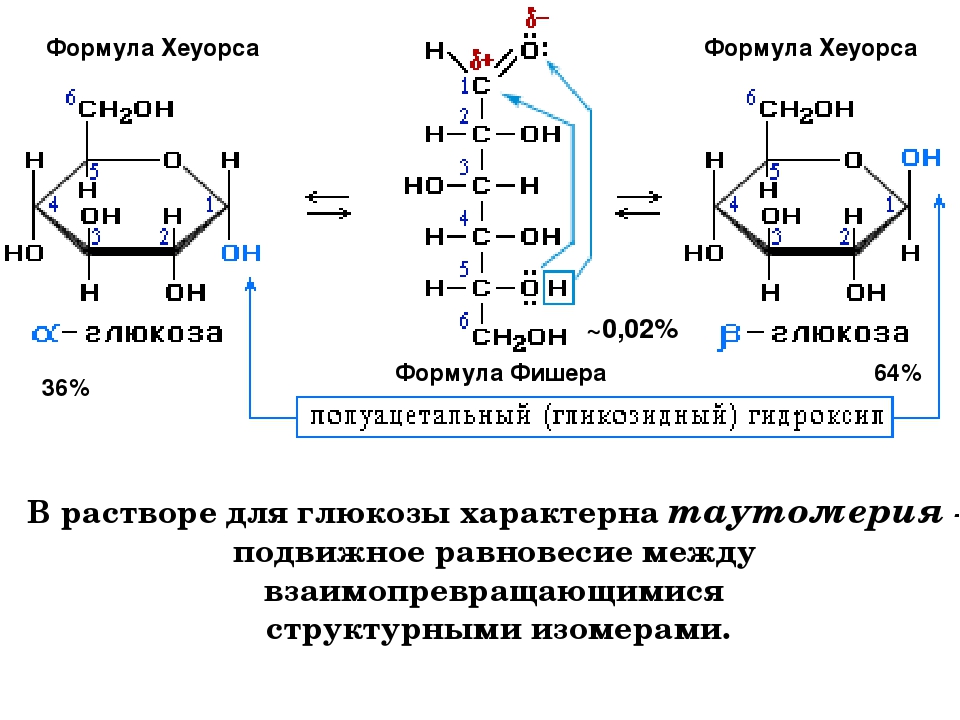 Преимущественно кристаллические, реже аморфные вещества, хорошо растворимые в воде и спирте.

Гликозиды представляют собой обширную группу органических веществ, встречающихся в растительном (реже в животном) мире и/или получаемых синтетическим путём. При кислотном, щелочном, ферментативном гидролизе они расщепляются на два или несколько компонентов — агликон и углевод (или несколько углеводов). Многие из гликозидов токсичны или обладают сильным физиологическим действием, например, гликозиды наперстянки, строфанта и другие.

N55

Фруктоза (фруктовый сахар), C₆H₁₂O₆ — моносахарид, кетоноспирт, кетогексоза, изомер глюкозы.

Физические свойства

Белое кристаллическое вещество, хорошо растворимое в воде. Температура плавления фруктозы ниже температуры плавления глюкозы. В 2 раза слаще глюкозы и в 4-5 раз слаще лактозы.

 

Химические свойства

 

В водных растворах фруктоза существует в виде смеси таутомеров, в которой преобладает β-D-Фруктопираноза и содержится, при 20 °C, около 20 % β-D-Фруктофуранозы и около 5 % α-D-Фруктофуранозы

В отличие от глюкозы и других альдоз, фруктоза неустойчива как в щелочных, так и кислых растворах; разлагается в условиях кислотного гидролиза полисахаридов или гликозидов

инфляция и связь с доходностью инвестиций

Ирвинг Фишер — американский экономист, представитель неоклассического направления в экономической науке. Родился 27 февраля 1867 года в Согертис, шт. Нью-Йорк. Он внес большой вклад в создание теории денег, а так же вывел «уравнение Фишера» и «уравнение обмена».

Его труды были взяты за основу современных методик для расчета уровня инфляции. Кроме того, они во многом помогли понять закономерности явления инфляции и ценообразования.

Полная и упрощенная формула Фишера

В упрощенном виде формула будет выглядит так:

i = r + π

Где:

• i — номинальная процентная ставка;
• r — реальная процентная ставка;
• π — темп инфляции.

Данная запись является приближенной. Чем меньше значения r и π, тем точнее выполняется это уравнение.

Более точной будет является такая запись:

r = (1 + i)/(1 + π) — 1 = (i — π)/(1 + π)

Количественная теория денег

Количественная теория денег — это экономическая теория, которая изучает воздействие денег на экономическую систему.

В соответствии с моделью, выдвинутой Ирвингом Фишером, государство должно регулировать объем денежных масс в экономике, чтобы избежать их недостатка или чрезмерного количества.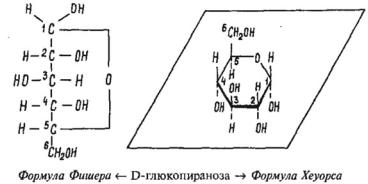

Согласно этой теории, явление инфляции возникает по причине несоблюдении этих принципов.

Недостаточное или чрезмерное количество денежной массы в обороте влечет за собой рост темпа инфляции.

В свою очередь рост инфляции предполагает рост номинальной процентной ставки.

• Номинальная процентная ставка отражает только текущую прибыль от вкладов без учета инфляции.
• Реальная процентная ставка — это номинальная ставка процента за вычетом ожидаемого уровня инфляции.

Уравнение Фишера описывает соотношения возникающие между этими двумя показателями и уровнем инфляции.

Видео

Советуем посмотреть данное видео, чтобы лучше разобраться в теории:

Как применять для расчета доходности инвестиции

Предположим, что вы делаете вклад в размере 10 000, номинальная процентная ставка составляет 10%, а уровень инфляции 5% в год.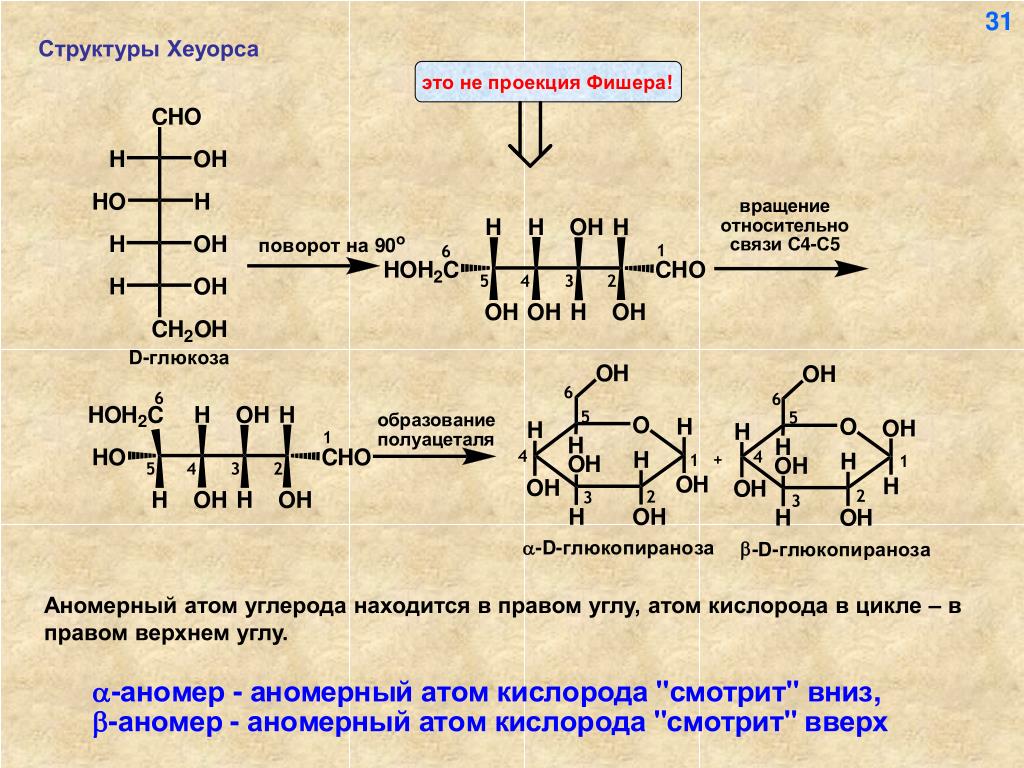 В таком случае реальная процентная ставка составит 10% — 5% = 5%. Таким образом, реальная процентная ставка тем меньше, чем выше уровень инфляции.

Именно эту ставку стоит учитывать, чтобы рассчитать количество денег, которое данный вклад принесет вам в будущем.

Типы начисления процентов

Как правило, начисления процентов прибыли происходит в соответствии с формулой сложного процента.

Сложный процент — это метод начисления процентов прибыли, при котором они прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.

Краткая запись формулы сложных процентов выглядит так:

K = X * (1 + %)ⁿ

Где:

• K — итоговая сумма;
• X — начальная сумма;
• % — процентное значение выплат;
• n — количество периодов.

При этом, реальный процент, который вы получите сделав вклад под сложные проценты, будет тем меньше, чем выше уровень инфляции.

При этом для любого вида инвестиций имеет смысл рассчитывать эффективную (реальную) процентную ставку: по своей сути это процент от начального вклада, который инвестор получит в конце срока инвестирования.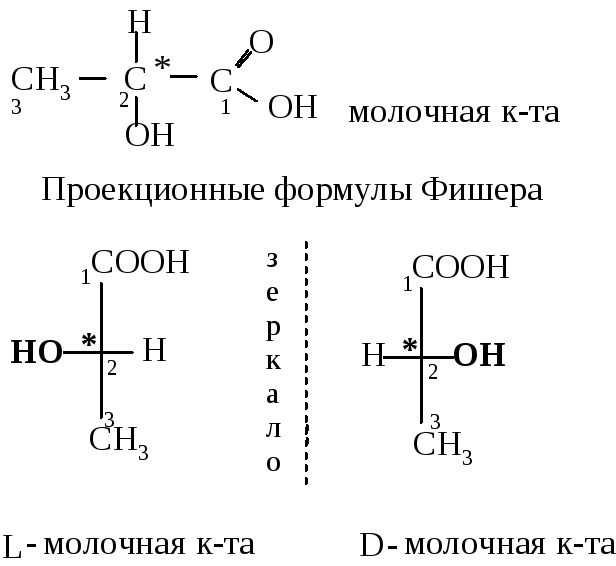 Проще говоря, это отношение полученной суммы к первоначально инвестированной сумме.

r(ef) = (P_n — P)/P

Где:

• r_ef — эффективный процент;
• Pn — итоговая сумма;
• P — начальный вклад.

Используя формулу сложных процентов получим:

r_ef = (1 + r/m) ^m — 1

Где m — количество начислений за период.

Международный эффект Фишера

Международный эффект Фишера — это теория обменного курса, выдвинутая Ирвингом Фишером. Суть этой модели заключается в расчете настоящих и будущих номинальных процентных ставок для того, чтобы определять динамику изменений курса обмена валют. Данная теория работает в чистом виде в том случае, если капитал свободно движется между государствами, валюты которых могут быть соотнесены друг с другом по стоимости.

Анализируя прецеденты роста инфляции в разных странах, Фишер заметил закономерность в том, что реальные процентные ставки, несмотря на рост количества денег не увеличиваются. Данное явление объясняется тем, что оба параметра со временем уравновешиваются посредством рыночного арбитража. Этот баланс соблюдается по той причине, что процентная ставка устанавливается с учетом риска инфляции и рыночных прогнозах по валютной паре. Это явление получило название эффект Фишера.

Экстраполировав эту теории на международные экономические отношения, Ирвинг Фишер сделал вывод, что изменение номинальных процентных ставок оказывает непосредственное влияние на подорожание или удешевление валюты.

Данная модель так и не была протестирована в реальных условиях. Основным её недостатком принято считать необходимость выполнения паритета покупательной способности (одинаковая стоимость аналогичных товаров в разных странах) для точного прогнозирования. И, к тому же, неизвестно, можно ли использовать международный эффект Фишера в современных условиях, с учетом колеблющихся курсов валют.

Прогнозирование инфляции

Явление инфляции заключается чрезмерном количестве, обращающихся в стране денег, что ведет к их обесцениванию.

Классификация инфляции происходит по признакам:

Равномерности — зависимости темпа инфляции от времени.

Однородности — распространения влияния на все товары и ресурсы.

Прогнозирование инфляции рассчитывается с помощью индекса инфляции и скрытой инфляции.

Основными факторами при прогнозировании инфляции являются:

• изменение курса валют;
• увеличение количества денег;
• изменение процентных ставок;

Также распространенным метод является расчет уровня инфляции на основе дефлятора ВВП. Для прогнозирования в этой методике фиксируют такие изменения в экономике:

• изменение прибыли;
• изменение выплат потребителям;
• изменение импортных и экспортных цен;
• изменение ставок.

Расчет доходности инвестиций с учетом уровня инфляции и без него

Доходностью инвестиций принято считать процентное отношение полученной прибыли к сумме начального взноса.

Формула доходности без учета инфляции будет выглядеть следующим образом:

X = ((P_n — P) / P )*100%

Где:

• X — доходность;
• P_n — итоговая сумма;
• P — начальный взнос;

В этом виде итоговая доходность рассчитывается без учета потраченного времени.

Для того, чтобы рассчитать доходность в процентах годовых, необходимо воспользоваться следующей формулой:

X_t = ((P_n — P) / P ) * (365 / T) * 100%

Где T — количество дней владения активом.

Оба способа не учитывают влияния инфляции на доходность.

Доходность с учетом инфляции (реальную доходность) следует рассчитывать по формуле:

R = (1 + X) / (1 + i) — 1

• R — реальная доходность;
• X — номинальная ставка доходности;
• i — инфляция.

Исходя из модели Фишера, можно сделать один главный вывод: инфляция не приносит доходов.

Повышение номинальной ставки вследствие инфляции никогда не будет больше, чем количество денег вложенных, которое обесценилось. Кроме того, высокий темп роста инфляции предполагает значительные риски для банков, и компенсация этих рисков лежит на плечах вкладчиков.

Применение формулы Фишера в международных инвестициях

Как можно заметить, в приведенных выше формулах и примерах, уровень высокий инфляции всегда снижает доходность инвестиций, при неизменной номинальной ставке.

Таким образом, основным критерием надежности инвестиции является не объем выплат в процентном выражении, а целевой уровень инфляции.

Подтверждением тому служит рейтинг стран, в которые поступает больше всего инвестиций. Первые места в нем занимают Китай и США. Рост инфляция в этих странах за последние 5 лет не превышал отметку в 3%.

Описание Российского инвестиционного рынка посредством формулы Фишера

Приведенная выше модель четко прослеживается на примере инвестиционного рынка РФ.

Падение инфляции в 2011-2013 году с 8.78% до 6.5% привело к повышению иностранных инвестиций: в 2008-2009 году они не превышали 43 млдр. долларов в год, а к 2013 достигли отметки в 70 млдр. долларов.

Резкое же повышение инфляции 2014-2015 привело к снижению иностранных инвестиций до исторического минимума. За эти два года сумма вложений в экономику России составила всего 29 млдр. долларов.

На данный момент, инфляция в России упала до 2.09%, что уже привело к притоку новых вложений от инвесторов.

В данном примере можно заметить, что в вопросах международного инвестирования основным параметром является именно реальная процентная ставка, расчет которой происходит по формуле Фишера.

Как рассчитывается индекс инфляции товаров и услуг

Индекс инфляции или индекс потребительских цен — это показатель, который отражает изменение цен товаров и услуг, покупаемых населением.

Численно индекс инфляции представляет собой отношение цен на товары в отчетный период к ценам на аналогичные товары базисного периода.

i_p = p₁ / p

Где:

• i_p — индекс инфляции;
• p₁ — цены на товары в отчетный период;
• p₂ — цены на товары в базисный период.

Проще говоря, индекс инфляции указывает на то, во сколько раз изменились цены за определенный промежуток времени.

Зная индекс инфляции, можно сделать вывод о динамике инфляции. Если индекс инфляции принимает значения больше единицы, то цены растут, а значит растет и инфляция. Индекс инфляции меньше единицы — инфляция принимает отрицательные значения.

Для прогнозирования изменений индекса инфляции используют следующие способы:

Формула Ласпейреса:

I_L = ( ∑p₁ * q _{) / ( ∑p0 * q0 )}

• I_L — индекс Ласпейреса;
• Числитель — суммарная стоимость товаров проданных в предыдущем периоде по ценам отчетного периода;
• Знаменатель — реальная стоимость товаров в предыдущем периоде.

Инфляции, при повышении цен, дается высокая оценка, а при их падении — заниженная.

Индекс Пааше:

Ip = ( ∑p₁ * q _{) / ( ∑p0 * q1 )}

Числитель — фактическая стоимость продукции отчетного периода;

Знаменатель — фактическая стоимость продукции отчетного периода.

Идеальный индекс цен Фишера:

I_p = √ ( ∑p₁ * q _{) / ( ∑p0 * q1 ) * ( ∑p1 * q ) / ( ∑p0 * q0 )}

 

Учет инфляции при расчете инвестиционного проекта

Учёт инфляции в таких инвестициях играет ключевую роль. Инфляции может повлиять на реализацию проекта в двух аспектах:

• В натуральном выражении — то есть, повлечь за собой изменение плана реализации проекта.
• В денежном выражении — то есть, повлиять на итоговою доходность проекта.

Способы влияния на инвестиционный проект в случае повышения инфляции:

1. Изменение валютных потоков в зависимости от инфляции;
2. Учет инфляционной премии в ставке дисконтирования.

Анализ уровня инфляции и её возможного влияния на инвестиционный проект требуют следующих мер:

• учет потребительского индекса;
• прогнозирование изменения индекса инфляции;
• прогнозирование изменения дохода населения ;
• прогнозирование объема денежных сборов.

Формула Фишера для расчета зависимости стоимости товаров от количества денег

В общем виде формула Фишера для расчета зависимости стоимости товаров от количества денег имеет следующую запись:

MV = PQ

Где:

• М — объем денежных масс в обороте;
• V — частота, с которой деньги используются;
• Р — уровень стоимости товаров;
• Q — количеств товаров в обороте.

Преобразовав эту запись, можно выразить уровень цен: P=MV/Q.

Главным выводом из данной формулы является обратная пропорциональность между стоимостью денег и их количеством. Таким образом, для нормального товарообращения в пределах государства, требуется контроль количества денег, находящихся в обороте.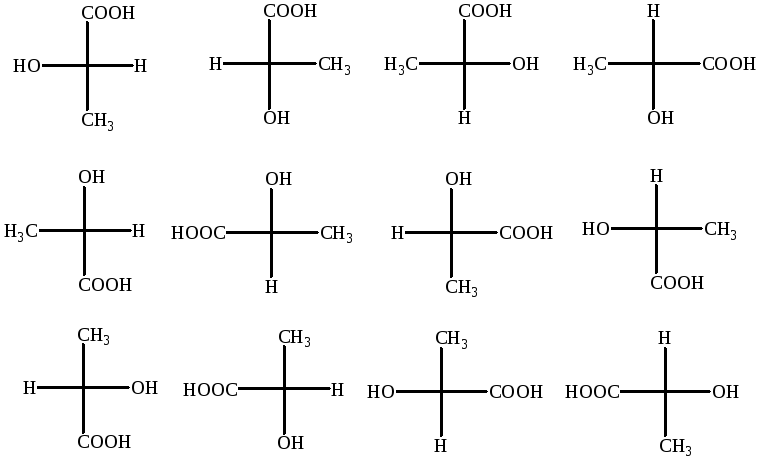 Повышения количества товаров и цен на них требует увеличения количества денег, а, в случае уменьшения этих показателей, следует уменьшать денежную массу. Такого рода регулирование объема денег в обращении возлагается на государственный аппарат.

Формула Фишера в применении к монопольному и конкурентному ценообразованию

Чистая монополия прежде всего предполагает, что один производитель полностью контролирует рынок и совершенной информированностью о его состоянии. Основной целью монополии является максимальная прибыль при минимальных расходах. Монополия всегда устанавливает цену выше значения предельных затрат, а объем выпуска ниже, чем в условиях совершенной конкуренции.

Присутствие на рынке производителя-монополиста как правило имеет серьезные экономические последствия: потребитель тратит больше денег, чем в условиях жесткой конкуренции, при этом рост цен происходит вместе с ростом индекса инфляции.

Если изменение этих параметров учесть в формуле Фишера, то мы получим увеличение денежной массы и постоянное уменьшение количества обращающихся товаров.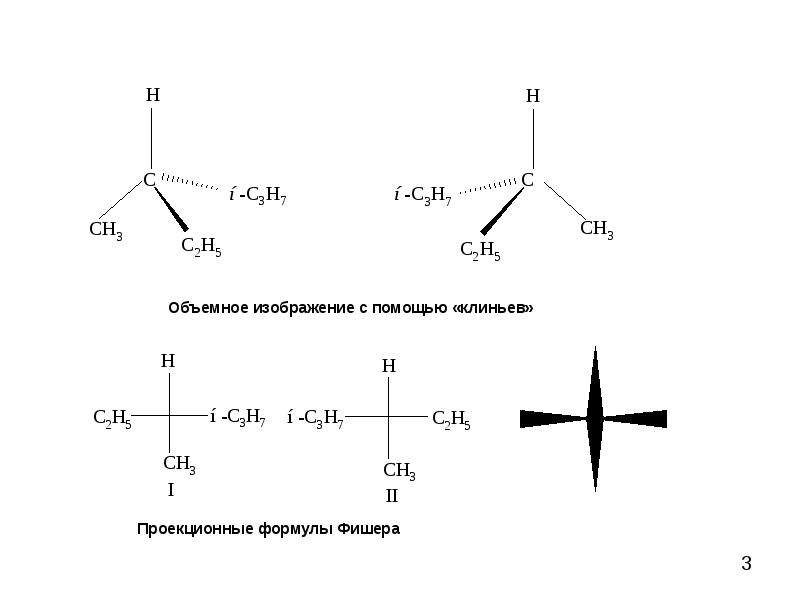 Такое положение приводит экономику к порочному циклу, в котором увеличение уровня инфляции ведет к увеличению только к увеличению цен, что в конце концов ещё больше стимулирует темп роста инфляции.

Конкурентный же рынок, в свою очередь, реагирует на повышение индекса инфляции совершенно другим образом. Рыночный арбитраж приводит к соответствию цен конъюктуре. Таким образом, конкуренция препятствует чрезмерному увеличению денежной массы в обороте.

Пример связи изменения процентных ставок с уровнем инфляции для России

На примере России, можно заметить прямую зависимость процентных ставок по вкладам от инфляции

Год	Процентная ставка, %	Инфляция, %
2017	9.75-7.75	2.09
2016	10.5-10.0	5.38
2015	15.0-11.0	12.91
2014	7.0-17.0	11.36

Таким образом видно, что нестабильность внешних условий и увеличение волатильности на финансовых рынках заставляет Центральный Банк снижать ставки, при повышении инфляции.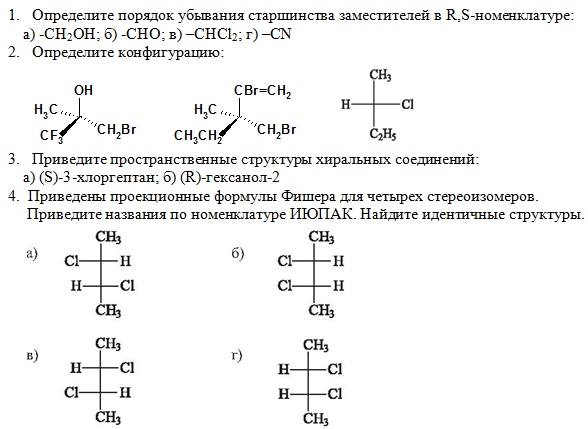

Формула Хеуорса (химия) для глюкозы, рыбозы, мальтозы, лактозы

Циклические формы моносахаридов, формулы Хеуорса

Оптическая изомерия

Моносахариды являются оптически активными веществами. Они содержат асимметрические атомы углерода. У глюкозы их четыре, у фруктозы – три. В результате этого  у моносахаридов имеется большое число стереоизомеров. Количество стереоизомеров глюкозы, имеющей четыре асимметрических атомов углерода,  рассчитывается по формуле: N=2n, N = 24 = 16 cтереоизомеров.

Из этого количества одна половина оптически деятельных стереоизомеров является антиподами другой половины. Таким образом, 16 стереоизомеров альдогексоз образуют  8 пар антиподов. Например, природному моносахариду Д-глюкозе соответствует антипод L-глюкоза (синтетически полученный).

Представить себе пространственное строение оптических изомеров альдоз удобнее всего, если выводить их из глицеринового альдегида. Он существует в виде двух  оптических изомеров (антиподов).

Пространственные конфигурации моносахаридов D- и  L-ряды.

Для более быстрого и удобного написания открытых форм моносахаридов Э. Фишер предложил изображать их проекционными формулами.

Углеродная цепь изображается вертикальной линией, на концах которой пишут первую и последнюю функциональные группы (альдегидную группу пишут всегда вверху). Группы Н и ОН пишут справа и слева от цепи, в соответствии с их пространственным расположением в молекуле.

Циклические формы моносахаридов

Давно были известны свойства моносахаридов, которые были не связаны со свойствами оксиальдегидов и оксикетонов, например:

• – наблюдалась повышенная реакционная способность одной из гидроксильных групп;
• – наличие в два раза больше изомеров, чем предсказывает формула Фишера
• – наблюдалось явление мутаротации – изменения угла вращения свежеприготовленных растворов и др.

В результате исследований было установлено, что в кристаллическом состоянии моносахариды имеют циклическое строение.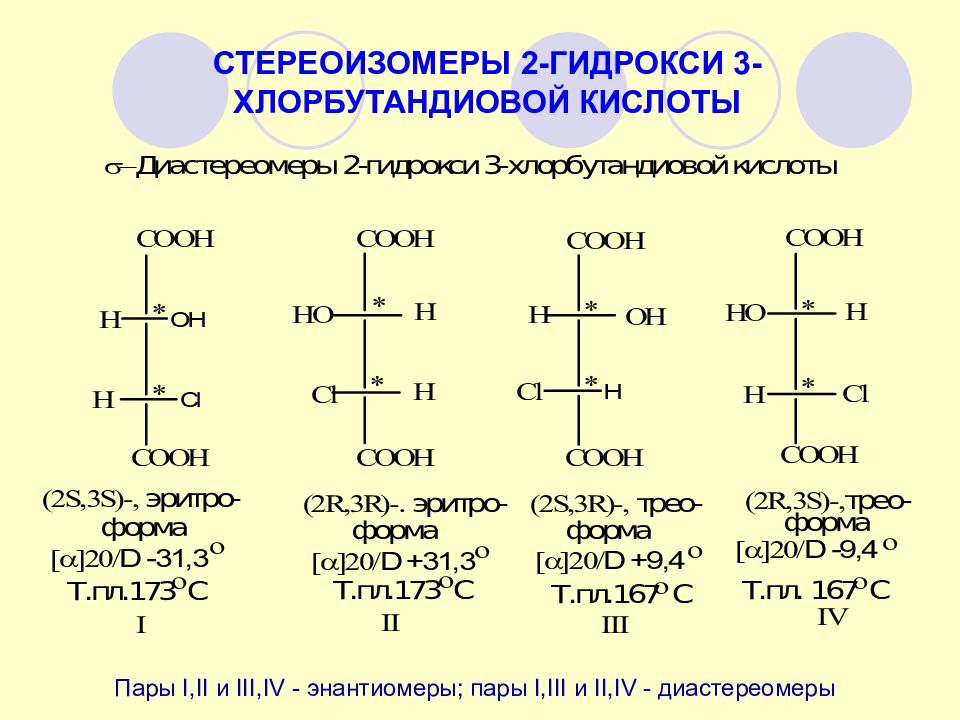 В растворах  моносахаридов наряду с альдегидными или кетонными формами всегда содержатся циклические полуацетальные формы (оксиформы ), причем содержание открытой оксо-формы мало (доли процента).

Циклические формы моносахаридов возникают в результате взаимодействия альдегидной (кетонной) группы с гидроксильной группой у пятого или у четвертого углеродного атома — кислород ОН-группы присоединяется к атому углерода карбонильной группы, а водород ОН-группы присоединяется к атому кислорода карбонильной группы.

Образуются устойчивые циклические полуацетальные формы — пиранозная (шестичленный цикл) либо фуранозная (пятичленный цикл). Эти формы получили название от соответствующих гетероциклических соединений, шестичленные — от пирана (точнее тетрагидропирана), а пятичленные — от фурана (точнее тетрагидрофурана). Гидроксил, образованный на месте бывшей карбонильной группы, называется полуацетальным или гликозидным и отличается по свойствам от спиртовых гидроксилов.

Для указания размера кольца в циклической форме моносахарида две последние буквы названия моносахарида (“оза”) заменяют окончанием “фураноза” в случае пятичленного кольца или “пираноза”- в случае шестичленного кольца, например, глюкопираноза, фруктофураноза, рибофураноза и т.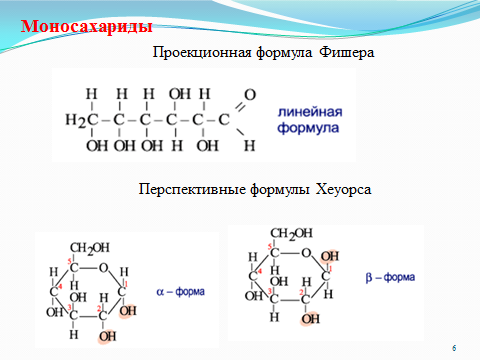 д.

В циклической форме монозы нет альдегидной или кетонной группы, имеются только гидроксильные группы. Эти гидроксилы разные: один гидроксил полуацетальный появился в результате внутримолекулярного взаимодействия карбонильной и спиртовой групп, для сахаров этот гидроксил называют еще гликозидным; остальные гидроксилы спиртовые.

Перспективные формулы Хеуорса

Для более удобного написания и наименования полуацетальных форм моноз Хеуорс предложил рассматривать их как производные гидрированных гетероциклов пирана и фурана:

Моносахариды, имеющие пятичленное кольцо, как у фурана, называют фуранозами. Имеющие шестичленное кольцо относят к производным пирана и называют пиранозами. Перед названием типа цикла пишут начальный слог наименования сахара, например α-D(+)-глюкопираноза, β-L(-)-рибофураноза и т. д.

Шестиугольники (пираны) и пятиугольники (фураны), изображенные в перспективе — цикл лежит в горизонтальной плоскости, связи, расположенные ближе к наблюдателю, изображаются более жирными линиями.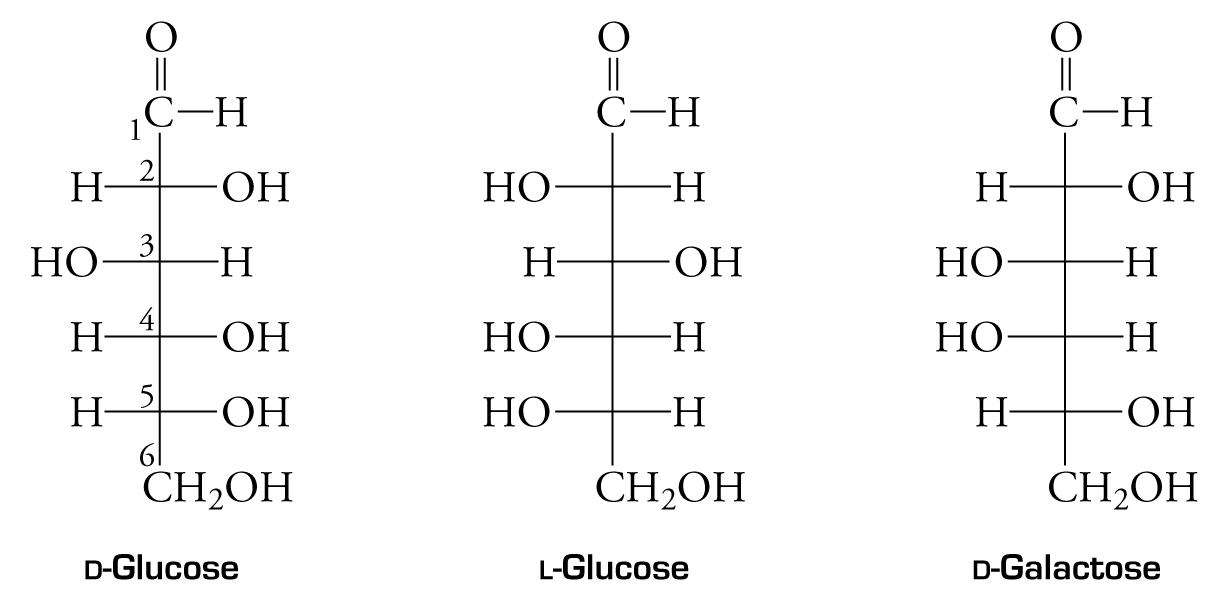

Атом кислорода располагается в шестичленном (пиранозном) цикле в правом верхнем углу, в пятичленном (фуранозном) – за плоскостью цикла, углеродные атомы, входящие в цикл, не пишутся, а только нумеруются от кислорода по часовой стрелке. Через атомы углерода проводят вертикальные линии, на концах которых пишут водородные атомы и ОН-группы.

Рассмотрим взаимоотношения проекционных формул Фишера и перспективных формул Хеуорса. Все группы (Н и ОН), расположенные справа в формуле Фишера, пишут под плоскостью цикла, а расположенные слева — над плоскостью цикла, концевая СН2-ОН группа располагается сверху от плоскости молекулы, если моносахарид относится к Д-ряду, и снизу от плоскости, если он относится к L-ряду.

Таким образом, в формулах Хеуорса полуацетальный гидроксил и концевая СН2-ОН группа располагаются у a-аномеров по разные стороны кольца, а у b-аномеров — по одну сторону (кружком обведены полуацетальные гидроксилы).

Аналогично можно осуществить переход  от формул Фишера к формулам Хеуорса на примере одного из аномеров фуранозной формы Д-фруктозы:

Цикло-цепные таутомеры моносахаридов

По мере изучения свойств моносахаридов выяснилось, что открытые (цепные) формулы не описывают полностью химическое поведение сахаров.

Например, несмотря на наличие в молекуле глюкозы пяти ОН– групп, только одна из них вступает в реакцию со спиртами в присутствии сухого хлористого водорода с образованием гликозидов. Для объяснения подобных противоречий было высказано предположение (1870 г. А. Колли; 1883 г. Б. Толленс), что истинное строение моноз не описывается лишь открытой (цепной) формулой.

Моносахариды образуют в водном растворе таутомерные смеси открытых и циклических форм. В основе их образования лежит внутримолекулярная реакция нуклеофильного присоединения спиртовых групп к альдегидной или кетонной группе:

H+ полуацетальный,

+ HOR или гликозидный

гидроксил

полуацеталь

Такой реакции способствует клешневидноя конформация углеродной цепи углевода:

В 1925–30 гг.

У. Хеуорс экспериментально определил размер возможных циклических таутомеров. Он предложил называть пятичленные циклы углеводов фуранозами, а шестичленные – пиранозами как производные фурана и пирана, соответственно:

фуран пиран

Пример.

Изобразите цикло-цепные таутомеры D-рибозы по Фишеру и Хеуорсу.

Пиранозные формы рибозы образуются путем взаимодействия гидроксильной группы при С5 рибозы с альдегидной группой:

b,D–рибопираноза D–рибоза a,D–рибопираноза

Образование циклической полуацетальной формы приводит к появлению нового хирального центра у первого атома углерода, в результате при такой циклизации получаются два диастереомера, которые отличаются конфигурацией только С1 атома и называются a— и b-аномерами.

В a- форме полуацетальный (гликозидный) гидроксил справа от углеродной цепи молекулы; он расположен с той же стороны, что и гидроксил, определяющий принадлежность углевода к D-ряду.

В b-форме эта группа с противоположной стороны, слева.

Аналогично, только с участием гидроксила при атоме С4, происходит образование фуранозных форм D-рибозы:

b,D–рибофураноза D–рибоза a,D–рибофураноза

Перспективные формулы Хеуорса

Недостатком проекционных формул Фишера является их несоответствие истинной геометрии молекулы.

Поэтому для циклических таутомеров были введены формулы Хеуорса, которые строятся по следующим правилам:

1. Написать формулу Фишера для цепной формы углевода.

2. Написать формулу для циклической таутомерной формы и пронумеровать атомы углерода в ней.

a,D–рибопираноза D–рибоза a,D–рибофураноза

(циклическая форма) (открытая форма) (циклическая форма)

Нарисовать необходимый цикл (5- или 6-членный) с атомом кислорода в правом верхнем углу и пронумеровать атомы углерода, связанные с кислородом, по часовой стрелке (см. рисунок)

4. Заместители, стоящие справа от цепи в проекции Фишера, располагают снизу от плоскости цикла, а стоящие слева – сверху.

Исключение составляют заместители у того углеродного атома, при котором происходит циклизация.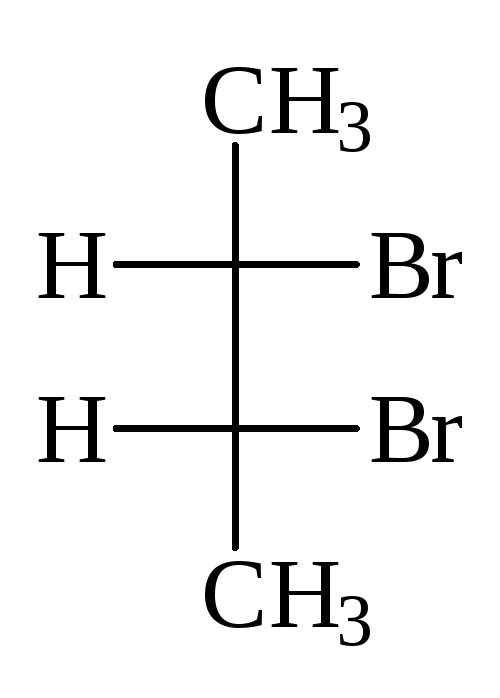

У такого атома углерода необходимо делать циклическую перестановку заместителей (см. рисунок).

a,D –рибопираноза ( по Хеуорсу ) a, D–рибофураноза (по Хеуорсу)

Цикло-цепная таутомерия моносахаридов – это существование в водном растворе смеси таутомерных форм, способных превращаться друг в друга через открытую таутомерную форму:

a,D-рибопираноза a,D-рибофураноза

18 % 16,5 %

D-рибоза

8,5 %

b,D-рибопираноза b,D-рибофураноза

51 % 6 %

Мутаротация сахаров

При растворении кристаллической таутомерной формы углевода в воде наблюдается явление мутаротации.

Мутаротация объясняется тем, что кристаллический циклический таутомер, растворяясь в воде, переходит постепенно через открытую форму во все другие таутомерные формы.При этом угол вращения плоскости поляризованного света будет меняться во времени до достижения равновесия между всеми цикло-цепными таутомерами.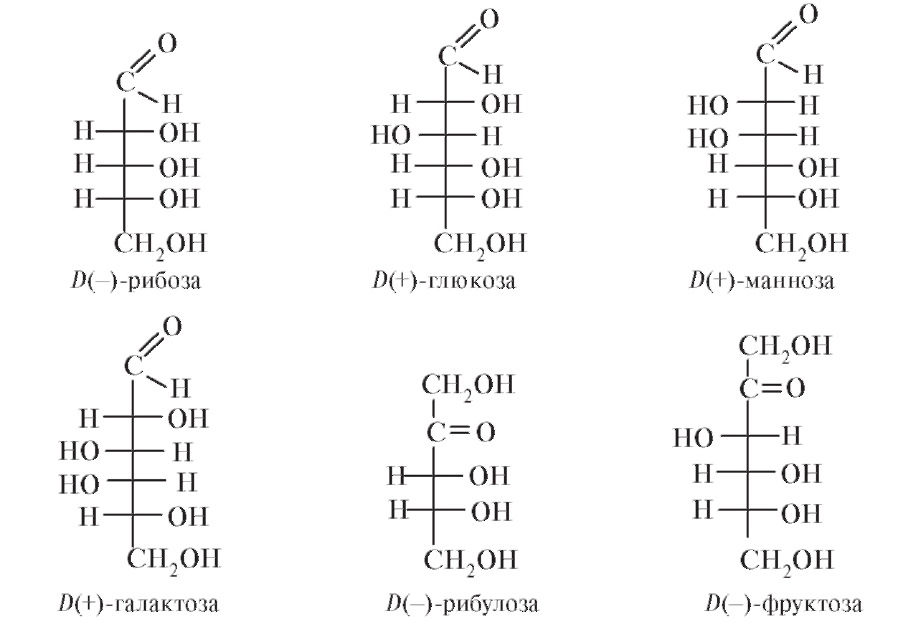

Это изменение во времени угла вращения плоскости поляризованного света в свежеприготовленных растворах сахаров называется мутаротацией.

Конформации моносахаридов

Углеводы в циклической форме существуют в виде неплоских конформаций. Так, для пиранозных форм наиболее энергетически выгодной является конформация «кресла».

В равновесной смеси таутомеров D-рибозы преобладает b,D-рибопираноза (51 %), так как этот таутомер существует в конформации кресла с экваториальным расположением большинства гидроксильных групп, что обеспечивает стабильность этой формы:

b, D–рибопираноза

Только одна ОН группа в третьем положении кольца занимает аксиальное положение в этой конформации.

В конформации a,D-рибопиранозы таких групп две – в первом и третьем

положениях:

a, D- рибопираноза

Эта форма менее стабильна; ее содержание составляет всего 18 %.

Пятичленные циклы и ациклическая форма содержатся в смеси в меньшей

концентрации.

Эпимеризация

Под действием щелочей некоторые моносахариды, отличающиеся конфигурацией одного хирального центра, могут превращаться друг в друга через промежуточное образование общей ендиольной формы:

D-глюкоза ендиол D-манноза

(63,5%) (2,5%)

D-фруктоза

(31%)

Стереоизомеры, отличающиеся конфигурацией одного хирального центра, называются эпимерами, а процесс их взаимного превращения друг в друга в щелочной среде – эпимеризацией.

Циклические формы моносахаридов.

Моносахариды открытой формы могут образовывать циклы, т.е. замыкаться в кольца.

Рассмотрим это на примере глюкозы.

Напомним, что глюкоза является шестиатомным альдегидоспиртом (гексозой).

В её молекуле одновременно присутствует альдегидная группа и несколькогидроксильных групп ОН (ОН — это функциональная группа спиртов).

При взаимодействии между собой альдегидной и одной из гидроксильных групп, принадлежащих одной и той же молекуле глюкозы, посленяя образует цикл, кольцо.

Атом водорода из гидроксильной группы пятого атома углерода переходит в альдегидную группу и соединяется там с кислородом.

Вновь образованная гидроксильная группа (ОН) называется гликозидной.

По своим свойствам она значительно отличается от спиртовых (гликозных)гидроксильных групп моносахаридов.

Атом кислорода из гидроксильной группы пятого атома углерода соединяется с углеродом альдегидной группы, в результате чего образуется кольцо:

Альфа- и бета-аномеры глюкозы различаются положением гликозидной группы ОНотносительно углеродной цепи молекулы.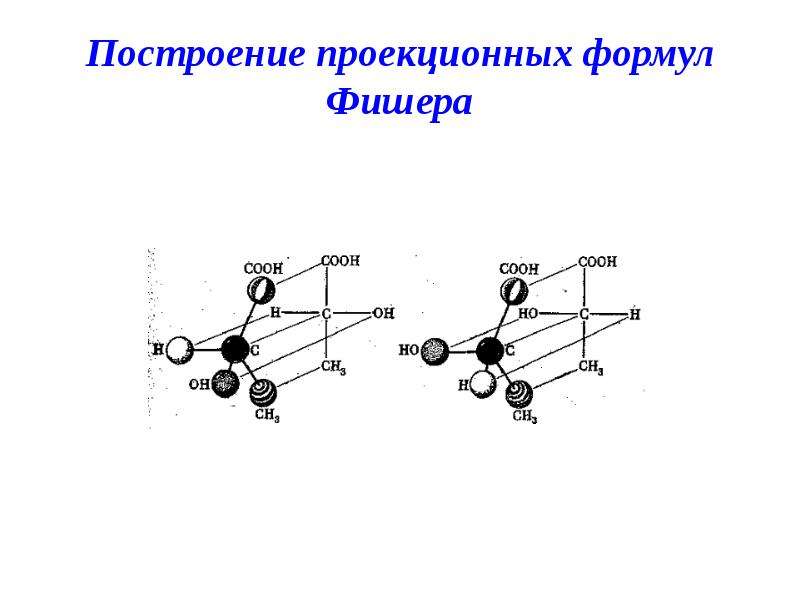

Мы рассмотрели возникновение шестичленного цикла.

Но циклы, также могут бытьпятичленными.

Это произойдёт в том случае, если углерод из альдегидной группы соединиться с кислородом гидроксильной группы при четвёртом атоме углерода, а не при пятом, как рассматривалось выше. Получится кольцо меньшего размера.

Шетичленные циклы называются пиранозными, пятичленные – фуранозными.

Названия циклов происходят от названий родственных гетероциклических соединений –фурана и пирана.

В названиях циклических форм наряду с названием самого моносахарида указывается «окончание» – пираноза или фураноза, характеризующие размер цикла.

Например: альфа-D-глюкофураноза, бета-D-глюкопираноза и т.д.

Циклические формы моносахаридов термодинамически более устойчивы в сравнении с открытыми формами, поэтому в природе они получили большее распространение.

Глюкоза

Глюкоза (от др.-греч. γλυκύς — сладкий) (C6h22O6) или виноградный сахар –важнейший из моносахаридов; белые кристаллы сладкого вкуса, легко растворяется в воде.

Глюкозное звено входит в состав ряда дисахаридов (мальтозы, сахарозы и лактозы) иполисахаридов (целлюлоза, крахмал).

Глюкоза содержится в соке винограда, во многих фруктах, а также в крови животных и человека.

Мышечная работа совершается, главным образом, за счёт энергии, выделяющейся при окислении глюкозы.

Глюкоза является шестиатомным альдегидоспиртом:

Глюкоза получается при гидролизе полисахаридов (крахмала и целюлозы) под действием ферментов и минеральных кислот.

В природе глюкоза образуется растениями в процессе фотосинтеза.

Фруктоза

Фруктоза или плодовый сахар С6Н12О6 – моносахарид, спутник глюкозы во многих плодовых и ягодных соках.

Фруктроза в качестве моносахаридного звена входит в состав сахарозы и лактулозы.

Фруктоза значительно слаще глюкозы.

Смеси с ней входят в состав мёда.

По строению фруктоза представляет собой шестиатомный кетоноспирт:

В отличие от глюкозы и других альдоз, фруктоза неустойчива как в щелочных, так и кислых растворах; разлагается в условиях кислотного гидролиза полисахаридов или гликозидов.

Галактоза

Галактоза — моносахарид, один из наиболее часто встречающихся в природе шестиатомных спиртов — гексоз.

Галактоза cуществует в ациклической и циклической формах.

Отличается от глюкозы пространственным расположением групп у 4-го атома углерода.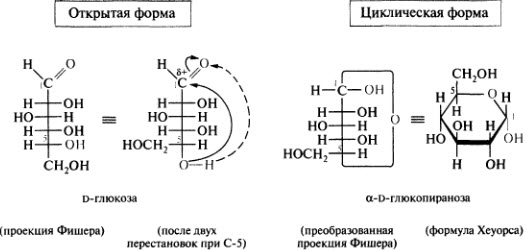

Галактоза хорошо растворима в воде, плохо в спирте.

В тканях растений галактоза входит в состав рафинозы, мелибиозы, стахиозы, а также в полисахариды — галактаны, пектиновые вещества, сапонины, различные камеди и слизи, гуммиарабик и др.

В организме животных и человека галактоза — составная часть лактозы (молочного сахара), галактогена, группоспецифических полисахаридов, цереброзидов и мукопротеидов.

Галактоза входит во многие бактериальные полисахариды и может сбраживаться так называемыми лактозными дрожжами.

В животных и растительных тканях галактозалегко превращается в глюкозу, которая лучше усваивается, может превращаться в аскорбиновую и галактуроновую кислоты.

Олигосахариды. Сахароза.

Олигосахариды – это один из видов полисахаридов.

Олигосахариды представляют собой углеводы, состоящие из нескольких моносахаридных остатков (от греч.

ὀλίγος — немногий).

Как правило, их молекулы содержат от 2 до 10 моносахаридных остатков и имеют относительно небольшую молекулярную массу.

Наиболее распространёнными из олигосахаридов являются дисахариды итрисахариды.

Дисахариды

Молекулы дисахаридов состоят из двух остатков моносахаридов.

Общая формула дисахаридов, как правило, C12h32O11.

Мальтоза + Н2О = D-глюкоза + D-глюкоза

Целлобиоза + Н2О = D-глюкоза + D-глюкоза

Лактоза + Н2О = D-глюкоза + D-галактоза

Сахароза + Н2О = D-глюкоза + D-фруктоза

Моносахариды: рибоза, дезоксирибоза, глюкоза, фруктоза. Понятие о пространственных изомерах углеводов. Циклические формы моносахаридов

Этим названием обозначаются широко распространенные в природе вещества.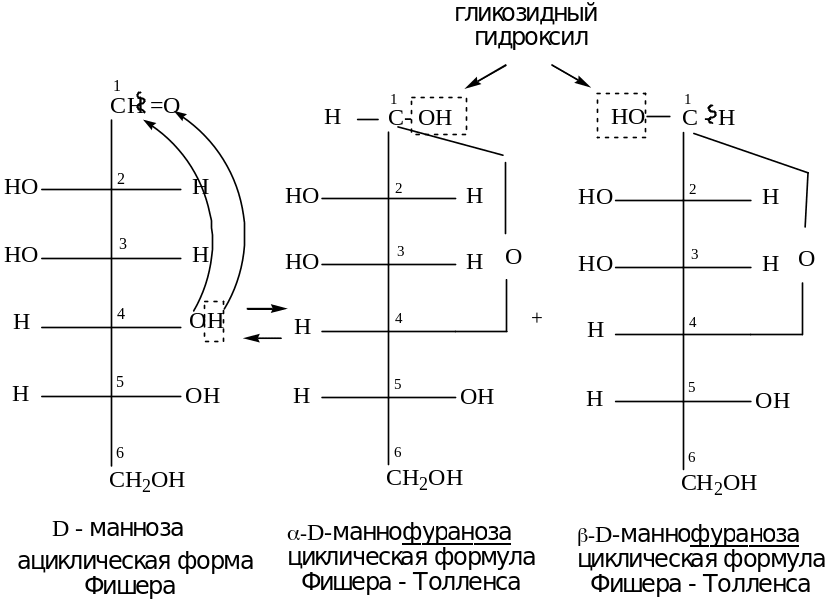 Они возникают в растительных организмах в результате сложной химической реакции, в которой участвуют вода, углекислый газ из воздуха и солнечная энергия, причем реакция происходит с участием зерен хлорофилла, находящегося в зеленой части растений.

Итак, углеводы (сахара) — одна из наиболее важных и распро­страненных групп природных органических соединений.

Общая формула Cmh3nOn(m и n³3).

В растительном организме до 80% (сухого веса), а в животных организмах — до 2% (сухого веса) составляют углеводы.

В организме животных и человека углеводы (сахара) поступа­ют с различными пищевыми продуктами растительного проис­хождения, т.к. сахара не могут синтезироваться в организмах животного происхождения.

В растениях же углеводы образуются в процессе фотосинтеза из воды и углекислого газа (см. выше):

Углеводы имеют разное строение, их можно разделить на две группы: простые и сложные углеводы.

Простыми углеводами (моносахаридами) называются такие соединения, которые не могут гидролизоваться с образованием более простых углеводов.

Сложными углеводами (полисахаридами) называют такие со­единения, которые могут гидролизоваться с образованием про­стых углеводов.

Моносахариды: рибоза, дезоксирибоза, глюкоза, фруктоза.

Понятие о пространственных изомерах углеводов.

Циклические формы моносахаридов

В молекулах моносахаридов может содержаться от трех до девяти атомов углерода. Названия всех групп моносахаридов, а также названия отдельных представителей оканчиваются на -оза. В зависимости от числа атомов углерода в молекуле моноса­хариды делятся на тетрозы, пентозы, гексозы и т.д. Наибольшее значение имеют гексозы и пентозы.

Рибоза и дезоксирибоза

В природе часто встречаются пентозы.

Из них большой инте­рес представляют рибоза и дезоксирибоза, т.к. они входят в состав нуклеиновых кислот.

Название «дезоксирибоза» показывает, что по сравнению с рибозой в ее молекуле на одну—ОН группу меньше.

Молекулы рибозы и дезоксирибозы могут иметь как линей­ное, так и циклическое строение:

Важнейшими представителями гексоз являются глюкоза и фруктоза, на примере которых рассмотрим строение, номенкла­туру, изомерию и свойства моносахаридов.

Строение

Глюкоза и фруктоза являются изомерами и имеют молеку­лярную формулу С6Н12О6.

Строение моносахаридов было установлено с помощью реакций:

1) Восстановления глюкозы йодистым водородом, в результате этой реакции образуется 2-иодгексан.

2) Глюкоза вступает в реакцию с аммиачным раствором оксида серебра, что говорит о наличии в молекуле глюкозы альдегид­ной группы:

(С5Н11О5)СОН+2[Ag(Nh4)2]OH®(C5h21O5)COONh5+2Ag¯+3Nh4+h3O

3) Глюкоза окисляется бромной водой в глюконовую кислоту:

(С5Н11О6)СОН+Br2+Н2O®(С5Н11O5)СООН+2HBr

4) При взаимодействии глюкозы с гидроксидом меди происходит окрашивание раствора в синий цвет — это качественная реак­ция для многоатомных спиртов.

Количественные эксперимен­ты показали, что в молекуле глюкозы 5 гидроксильных групп. Таким образом, глюкоза — это пятиатомный альдегидоспирт.

5) В молекуле фруктозы также установлено наличие 5 спиртовых групп, но при энергичном окислении фруктоза образует две оксикислоты с двумя и четырьмя атомами углерода.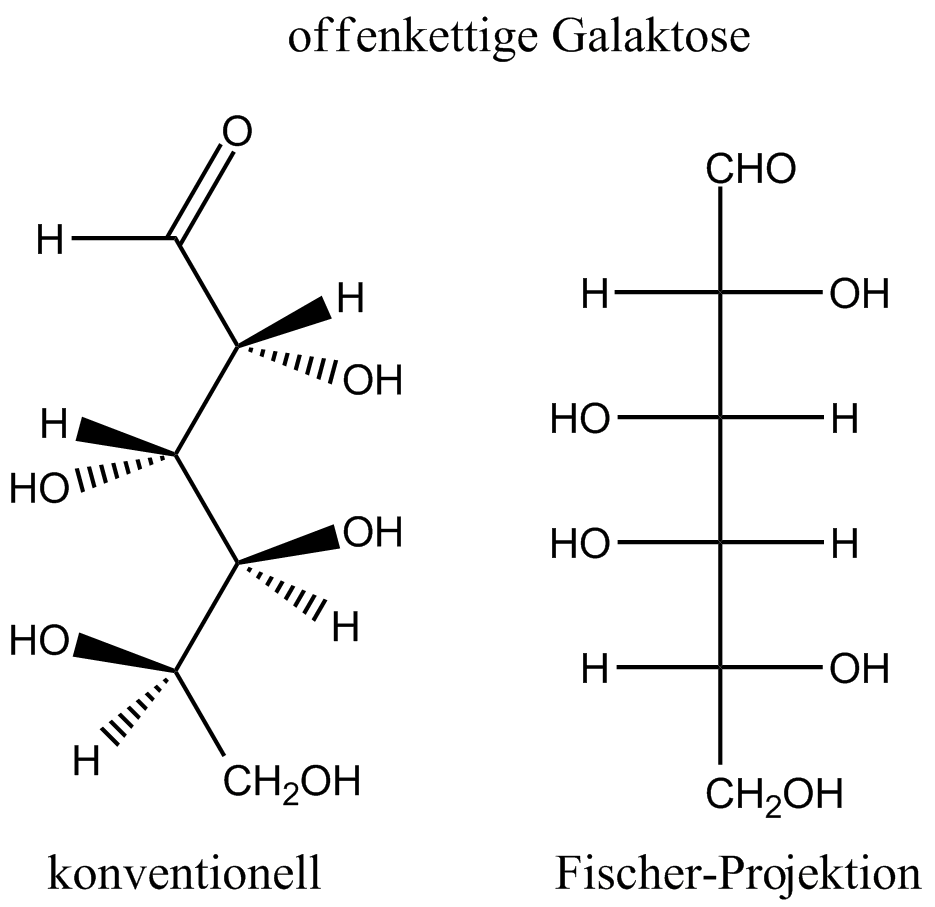 Такое поведение характерно для кетонов.

Таким образом, фрукто­за — многоатомный кетоноспирт:

Следовательно, моносахариды — это многоатомные альдегидо- или кетоноспирты.

Однако ряд экспериментальных фактов не находит объясне­ния в рамках такого строения моносахаридов: 1) моносахариды не дают некоторые реакции, характерные для альдегидов; в частности, они не образуют бисульфитных соеди­нений при взаимодействии с NaHSO3;

2) при измерении оптической активности свежеприготовленных растворов глюкозы оказалось, что она с течением времени па­дает;

3) при нагревании моносахаридов с метиловым спиртом в присут­ствии HСl выпадает кристаллический осадок гликозида, кото­рый легко гидролизуется с образованием одной молекулы спирта.

Все эти факты нашли объяснение, когда предположили, что каждый моносахарид может существовать в виде несколь­ких таутомерных форм.

В растворе, кроме развернутых цепей, существуют и циклические формы, которые образуются при внутримолекулярном взаимодействии альдегидной группы и гидроксильной группы при пятом атоме углерода:

Наличие циклической формы объясняет все вышеприведен­ные аномалии следующим образом:

1) в растворах преобладают циклические формы моносахаридов, открытые формы находятся в небольших количествах;

2) изменение оптической активности связано с установлением равновесия между открытой и циклической формами.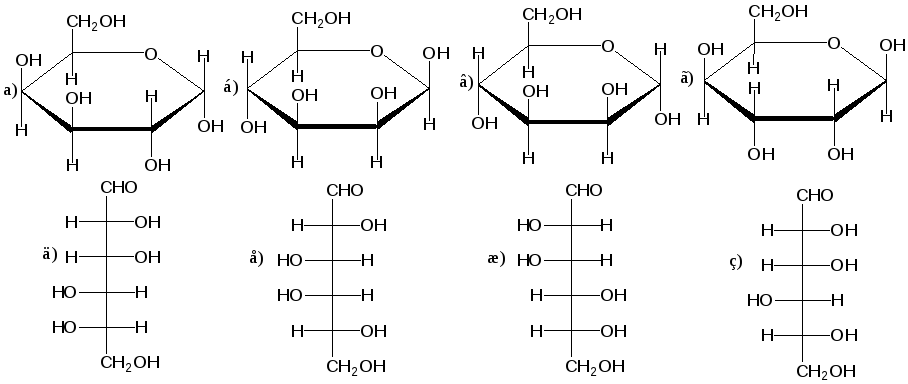

Образование гликозидов объясняется наличием гликозидного, или полуацетального гидроксила, который отличается большей ре­акционной способностью, чем остальные гидроксиды.

Поэтому он легко взаимодействует со спиртами с образованием гликозидов. Хеуорс предложил изображать циклические формы Сахаров так, чтобы отчетливо были видны и кольцо, и заместители:

Циклические формы моносахаридов могут содержать пять или шесть атомов в цикле.

Сахара с шестичленным циклом назы­ваются пиранозами, например, глюкоза — глюкопираноза; цик­лические формы Сахаров с пятичленным циклом называются фуранозами. Глюкоза с пятичленным циклом — глюкофураноза, а фруктоза с пятичленным циклом — фруктофураноза.

Номенклатура и изомерия моносахаридов Названия моносахаридов содержат греческие названия числа атомов и окончание -оза (см. выше).

Наличие альдегидной и кетонной группы обозначается прибавлением слов альдоза, кетоза.

Глюкоза — альдогексоза, фруктоза — кетогексоза.

Изомерия обусловлена наличием:

1) альдегидной или кетонной группы;

2) асимметричного атома углерода;

3) таутомерии (т.е. равновесия между разными формами молекулы).

Получение моносахаридов

1) В природе глюкоза и фруктоза (наряду с другими моносахари­дами) образуются в результате реакции фотосинтеза:

Исходя из этого можно сделать вывод, что ряд моносахаридов встречается в природе в свободном виде, например фруктоза и глюкоза содержатся в фруктах, фруктоза — в меде и т.д.

2) Гидролиз полисахаридов.

Например, на производстве глюкозу чаще всего получают гидролизом крахмала в присутствии сер­ной кислоты:

О связи формулы Гордона с формулой Фишера Текст научной статьи по специальности «Экономика и бизнес»

3 (15) — 2009

Оценка стоимости бизнеса

О СВЯЗИ ФОРМУЛЫ ГОРДОНА С ФОРМУЛОЙ ФИШЕРА

А. Г. ПЕРЕВОЗЧИКОВ,

доктор физико-математических наук, профессор, академик РАЕН, директор по производству ООО «РАО КЭС»,

г. Тверь

В настоящей работе рассматривается задача определения постпрогнозной стоимости бизнеса для метода дисконтирования денежного потока (ДДП) в рамках доходного подхода [1]. Показано, что известная формула Гордона [1] для постпрогнозной стоимости бизнеса может быть получена из известной формулы для стоимости бесконечного аннуитета и ставки доходности для эквивалентного постоянного денежного потока, которая получается по известной формуле Фишера [1]. Тем самым получено новое доказательство формулы Гордона, выявляющее ее экономический смысл, и одновременно установлена связь между известными формулами Гордона и Фишера, которые ранее считались независимыми. Рассматривается числовой пример.

1. Метод ДДП

1.1. Основные модели денежного потока

Существуют два основных вида денежных потоков [1].

— Денежный поток для собственного капитала или бездолговой денежный поток.

— Денежный поток для собственного капитала.

Денежный поток на инвестированный капитал

равен прибыли до налогообложения и уплаты процентов (EBITDA [2]), скорректированной на ставку налога на прибыль с = 0,24, плюс амортизация, минус капвложения и изменение чистого оборотного капитала.

Дальше за основу берется бездолговой денежный поток, величина которого будет обозначаться

через = 1,2,…,п, где п — длительность прогнозного периода, выраженная в годах.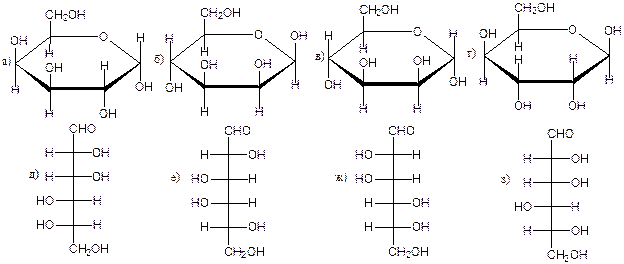 + = 1,2,…

Здесь ДZt = 21 — 21 -1 — изменение задолженности,

g — ставка дисконта на заемный капитал, определяемая обычно средней ставкой по кредитам предприятиям и организациям на дату оценки по данным Банка России соответствующей длительности,

р1 = 0,76gZt — — платежи по кредитам на конец ¿-го года, включающие проценты, скорректированные на ставку налога на прибыль, и изменение основной суммы долга ДZt.

Если новые кредиты не берутся, то ДZt < 0 , и с учетом знака минус величина погашенной части основной суммы долга будет входить с плюсом в платежи по кредитам р(. Возможен и случай ДZt > 0, это соответствует получению нового кредита на конец ¿-го года в размере > 0 . Так бывает, когда заемщику представляется не отдельный кредит, а кредитная линия. В этом случае он может брать и погашать кредиты.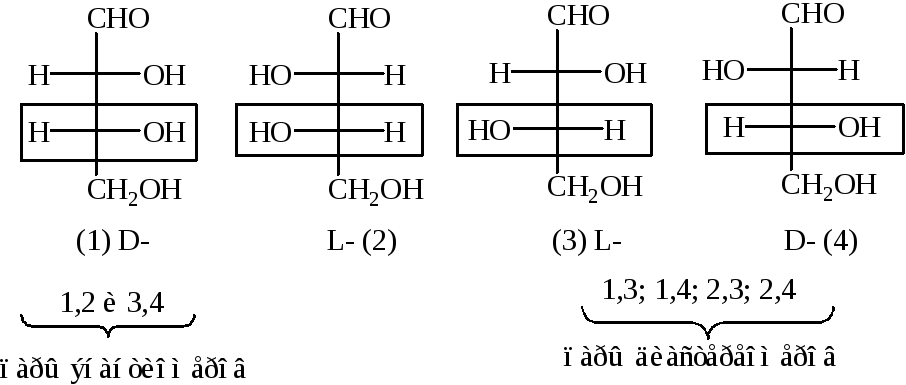 Единственное условие состоит в том, что сумма остатков долга по всем займам в любой момент времени не должна превышать установленного лимита по кредитной линии, и все

3 (15) — 2009

Оценка стоимости бизнеса

кредиты должны быть погашены к концу п-го года, т. е. последнего прогнозного года.

Заметим, что величины ДZt могут быть положительны. Это означает новый заем величины ДZt. 1.2. Ставки дисконта на собственный и инвестированный капитал Обозначим через i подходящую ставку дисконта на собственный капитал. Ставка дисконта на собственный капитал представляет собой ставку дохода на вложенный капитал, достижение которой ожидает инвестор при принятии решения о приобретении будущих доходов (например, будущего денежного потока) с учетом риска их получения.

При расчете ставки дисконта обычно используется модифицированная модель оценки капитальных активов (САРМ). + 5з, где Rf — безрисковая ставка,

в — коэффициент бета компании, Rm — доходность рынка,

— премия за страновой риск,

S2 — премия за малую капитализацию,

— премия за специфический риск оцениваемой компании.

Если объединить все корректировки к обычной модели САРМ в одну, введя суммарную поправку:

й = Sl + £2 + £3,

то основную формулу модифицированной модели САРМ можно записать в виде:

7 = Яг +р.(Ят -яг) + й. (1)

Пусть w — доля заемного капитала в инвестированном капитале компании, определенном по рыночной стоимости, характеризующая структуру капитала. 7 = , определяемые по формулам (1), (2), т. е. бета компании и соответствующие ставки дисконта являются функциями времени.

Кроме ставки на собственный и заемный капитал рассматривается средневзвешенная ставка ], характеризующая доходность инвестированного капитала (МАСС). Средневзвешенная стоимость капитала учитывает в себе все риски, связанные с финансированием деятельности предприятия, как из собственных источников финансирования так и за счет заемных средств. Стоимость финансирования деятельности предприятия за счет собственного капитала (стоимость собственного капитала) отражает все риски, присущие инвестициям в виде акционерного капитала, в то время как стоимость финансирования за счет заемных средств выражается в процентной ставке, по которой предприятию предоставляют кредитные ресурсы.

Средневзвешенная стоимость капитала рассчитывается по формуле [1]:

У = (1-е) gw+i (1^).

(3)

(4)

£ (1 + (1 + ])п Если w = wt,t = 1,2,…,п, то в = вt,i = *г,3 = Л зависят от дискретного времени.

Постпрогнозная стоимость собственного капитала получается по формуле:

Хп = (1 — wn)Yn ,

(5)

где wn — целевая структура капитала, которая рассчитывается на основе рыночных данных по отрасли и считается неизменной в постпрогнозный стационарный период.

Оценка стоимости бизнеса

3 (15) — 2009

Для постпрогнозной стоимости инвестируемо го капитала используется формула Гордона [1]:

1п(1 + Vп+1)

(6)

]п+1 Vn+1

: 0 = 1 + ]п + 1 — 1 •] п+1

1 + к+1

(7)

Г„ =

}п+1

1 + Jn+1

1 + V,

-1

Чп(1 + Vn+1 ) ]п+1 — Vn+1

(10)

п+1

где уп+1 — постпрогнозный темп изменения денежного потока на инвестированный капитал, который считается постоянным в силу предположения о стационарности постпрогнозного периода. = -1 = -1 = 0.098 = 9,!

1 + V,

п +1

1,02

Откуда по формуле (10) имеем:

Г„ =

1п

]п+1

100 0.098

= 1020.

Как обычно, в модели ДДП [3] предполагается выполненным условие корректности модели бесконечного роста:

К+1| < Л+1. (8)

Это условие обеспечивает сходимость бесконечного ряда для текущей стоимости постпрогнозного денежного потока (ДП). = п + 1,п + 2,… то эквивалентная ставка (7) представляет собой ставку для эквивалентного постоянного реалистического денежного потока. Таким образом, мы расширяем экономический смысл формулы Фишера на рост ДП любой природы.

3. Новое доказательство формулы Гордона на основе эквивалентной ставки

Воспользуемся формулой для аннуитета эквивалентного постоянного ДП [1]:

Мы видим, что полученные значения совпадают, что и требовалось доказать.

В заключение отметим, что в настоящей работе показано, как известная формула Гордона для постпрогнозной стоимости бизнеса может быть получена из известной формулы для стоимости бесконечного аннуитета и ставки доходности для эквивалентного постоянного денежного потока, которая получается по известной формуле Фишера. Тем самым получено новое доказательство формулы Гордона, выявляющее ее экономический смысл, и одновременно установлена связь между известными формулами Гордона и Фишера, которые ранее считались независимыми.

Список литературы

1. Оценка бизнеса: Учебник / Под ред. А. Г. Гряз-новой, М. А. Федотовой. М.: Финансы и статистика. 2002.

2. Методология и руководство по проведению оценки бизнеса и/или активов ОАО РАО «ЕЭС России» и ДЗО ОАО РАО «ЕЭС России». Deloitte&Touche. Декабрь 2003 — март 2005.

3. Перевозчиков А. Г. Учет структуры капитала в моделях денежного потока для собственного и инвестированного капитала. Аудит и финансовый анализ, № 1, 2006. С.163-166.

7х»

67

1

1

п

п

Проекционная формула — фишер — Большая Энциклопедия Нефти и Газа, статья, страница 1

Проекционная формула — фишер

Cтраница 1

Проекционная формула Фишера для натрийрубидиевой соли () — винной кислоты означает, что атомы главной цепи, расположенной вертикально, находятся за плоскостью соответствующих асимметричных атомов углерода, а атомы и группы атомов по линии, перпендикулярной главной цепи, находятся перед плоскостью, в которой расположены рассматриваемые асимметричные атомы углерода.  [1]

Проекционные формулы Фишера представляют собой условный способ изображения молекул с хиральными центрами. В них четыре связи С-атома изображают в плоскости под прямыми углами. В действительности же заместители справа и слева от хирального центра находятся перед плоскостью бумаги, верхний и нижний заместители — за этой плоскостью.  [2]

Нарисуйте проекционные формулы Фишера для каждого из приведенных ниже соединений, имея в виду ( в тех случаях, когда это необходимо), что в-и L-изомеры с двумя или большим числом асимметрических углеродных атомов всегда представляют собой не диастереомеры, а энантиомеры. Используется система глицеринового альдегида во всех случаях, за исключением специально оговоренного.  [3]

Нарисуйте проекционные формулы Фишера для каждого из приведенных ниже соединений, имея в виду ( в тех случаях, когда это необходимо), что D — и ь-изомеры с двумя или большим числом асимметрических углеродных атомов всегда представляют собой не диастереомеры, а энантиомеры. Используется система глицеринового альдегида во всех случаях, за исключением специально оговоренного.  [4]

Нарисуйте проекционные формулы Фишера для каждого из приведенных ниже соединений, имея в виду ( в тех случаях, когда это необходимо), что в-и ь-изомеры с двумя или большим числом асимметрических углеродных атомов всегда представляют собой не диастереомеры, а энантиомеры. Используется система глицеринового альдегида во всех случаях, за исключением специально оговоренного.  [5]

Если некая проекционная формула Фишера не имеет младшего заместителя сверху или снизу от хирального центра, то ее следует переписать без изменения конфигурации, используя один из приводимых ниже способов.  [6]

Постройте проекционные формулы Фишера эпаптномеров 2-ами-нопропаповоп, 2 — амп11О — 3 — п1дроксппропаповоп и 2-хлорпропаповой кислот.  [7]

Изображение проекционных формул Фишера требует соблюдения ряда правил.  [8]

Взаимосвязь проекционных формул Фишера открытых цепей Сахаров и формул Хеуорса кольцевых форм Сахаров показана ниже на примере D-ГЛЮКОЗЫ и ее пиранозной кольцевой формы.  [9]

В проекционной формуле Фишера выполняется четное число перестановок так, чтобы заместитель, имеющий номер 4, оказался внизу вертикальной линии ( связь по вертикали направлена от наблюдателя.  [10]

В проекционной формуле Фишера соединений эритро-ряда идентичные или подобные группы расположены по одну сторону, в то время как в реальной молекуле такие группы будут расположены по разные стороны, так как для молекулы энергетически более выгодна заторможенная конформация, а проекционная формула изображает молекулу в заслоненной конформации.  [11]

В проекционных формулах Фишера применяют специальные условности и ограничения. Хиральный атом углерода, лежащий в центре на плоскости бумаги, связан направо и налево с атомами или группами, которые рассматриваются как направленные к наблюдателю, а атомы и группы, связи к которым идут от хирального атома вверх и вниз, рассматриваются как идущие за плоскость бумаги. Главная цепь, если она имеется, располагается вертикально; атом, имеющий наименьший локант, помещается наверху.  [12]

В проекционных формулах Фишера все связи пишутся в плоскогт оу-маги. Ось вращения молекулы ориентирована вертикально, а атомы водорода и птдроксильные группы размещаются слева и справа. Эти плоские формулы соответствуют трехмерным моделям, в которых горизонтальные связи расположены над плоскостью, а вертикальные — в плоскости бумаги пли под ней. Ниже приведены стереоизомеры XXIV, изображенные посредством формул Фишера.  [13]

В проекционных формулах Фишера все связи пишутся в плоскости бумаги. Ось вращения молекулы ориентирована вертикально, а атомы водорода и гидроксильные группы размещаются слева и справа. Эти плоские формулы соответствуют трехмерным моделям, в которых горизонтальные связи расположены над плоскостью, а вертикальные — в плоскости бумаги или под ней. Ниже приведены стереоизомеры XXIV, изображенные посредством формул Фишера.  [14]

Для удобства проекционные формулы Фишера представлены таким образом, что группы, обычно расположенные направо от углеродной цепочки, здесь расположены под ней.  [15]

Страницы:      1    2    3    4

Уравнение Фишера — обзор, формула и пример

Что такое уравнение Фишера?

Уравнение Фишера — это экономическая концепция, описывающая взаимосвязь между номинальными и реальными процентными ставками под влиянием инфляции Инфляция Инфляция — это экономическая концепция, которая относится к повышению уровня цен на товары в течение определенного периода времени. Повышение уровня цен означает, что валюта в данной экономике теряет покупательную способность (то есть за ту же сумму денег можно купить меньше).. Уравнение утверждает, что номинальная процентная ставка равна сумме реальной процентной ставки плюс инфляция.

Уравнение Фишера часто используется в ситуациях, когда инвесторы или кредиторы просят дополнительное вознаграждение для компенсации потерь покупательной способности из-за высокой инфляции.

Концепция широко используется в области финансов и экономики. Он часто используется при расчете окупаемости инвестиций. Возврат инвестиций (ROI). Рентабельность инвестиций (ROI) — это показатель эффективности, используемый для оценки окупаемости инвестиций или сравнения эффективности различных инвестиций.или в прогнозировании поведения номинальных и реальных процентных ставок. Один из примеров — когда инвестор хочет определить фактическую (реальную) процентную ставку, полученную по инвестициям, после учета влияния инфляции.

Один интересный вывод уравнения Фишера связан с денежно-кредитной политикой. Денежно-кредитная политика. Денежно-кредитная политика — это экономическая политика, которая управляет размером и темпами роста денежной массы в экономике. Это мощный инструмент. Уравнение показывает, что денежно-кредитная политика движет инфляцию и номинальную процентную ставку в одном направлении.Принимая во внимание, что денежно-кредитная политика обычно не влияет на реальную процентную ставку.

Американский экономист Ирвинг Фишер предложил уравнение.

Формула уравнения Фишера

Уравнение Фишера выражается следующей формулой:

(1 + i) = (1 + r) (1 + π)

Где:

i — номинальная процентная ставка ставка

r — реальная процентная ставка

π — уровень инфляции

Однако можно также использовать приблизительную версию предыдущей формулы:

i ≈ r + π

Пример уравнения Фишера

Предположим, Сэм владеет инвестиционным портфелем.В прошлом году доходность портфеля составила 3,25%. Однако в прошлом году инфляция составляла около 2%. Сэм хочет определить реальную прибыль, которую он получил от своего портфеля. Чтобы найти реальную норму прибыли, мы используем уравнение Фишера. Уравнение утверждает, что:

(1 + i) = (1 + r) (1 + π)

Мы можем изменить уравнение, чтобы найти реальную процентную ставку:

Следовательно, реальная процентная ставка , или фактическая доходность инвестиций, портфеля равна:

Реальный процент, который инвестиционный портфель Сэма заработал в прошлом году с учетом инфляции, составляет 1.26% .

Дополнительная литература

CFI предлагает программу сертификации аналитика финансового моделирования и оценки (FMVA) ® Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® для тех, кто хочет вывести свою карьеру на новый уровень. Чтобы продолжить обучение и продвигаться по карьерной лестнице, вам будут полезны следующие ресурсы CFI:

• Эффективная годовая процентная ставка Эффективная годовая процентная ставка Эффективная годовая процентная ставка (EAR) — это процентная ставка, которая корректируется с учетом начисления сложных процентов за определенный период.Проще говоря, эффективная
• плавающая процентная ставка Плавающая процентная ставка Плавающая процентная ставка относится к переменной процентной ставке, которая изменяется в течение срока долгового обязательства. Это противоположность фиксированной ставки.
• Премия за рыночный риск Премия за рыночный риск Премия за рыночный риск — это дополнительная прибыль, которую инвестор ожидает от владения рискованным рыночным портфелем вместо безрисковых активов.
• Нормативная экономика Нормативная экономика Нормативная экономика — это школа мысли, которая считает, что экономика как предмет должна передавать оценочные заявления, суждения и мнения по

Номинальным и реальным процентным ставкам

16.14 Уравнение Фишера: номинальные и реальные процентные ставки

Когда вы занимаетесь или ссужаете взаймы, вы обычно делаете это в долларовом эквиваленте. Если вы берете ссуду, ссуда выражается в долларах, а обещанные вами платежи — в долларах. Эти долларовые потоки необходимо скорректировать с учетом инфляции, чтобы рассчитать выплаты в реальном выражении. То же самое справедливо и для кредитора: вам необходимо рассчитать процент, который вы зарабатываете на сбережениях, с поправкой на инфляцию.

Уравнение Фишера обеспечивает связь между номинальной и реальной процентной ставкой.Для преобразования номинальных процентных ставок в реальные мы используем следующую формулу:

реальная процентная ставка ≈ номинальная процентная ставка — уровень инфляции.

Чтобы найти реальную процентную ставку, мы берем номинальную процентную ставку и вычитаем уровень инфляции. Например, если процентная ставка по ссуде составляет 12 процентов, а уровень инфляции составляет 8 процентов, то реальная доходность по этой ссуде составляет 4 процента.

При расчете реальной процентной ставки мы использовали фактический уровень инфляции.Это уместно, если вы хотите понять реальную процентную ставку, фактически выплаченную по кредитному договору. Но на момент заключения кредитного соглашения уровень инфляции, который произойдет в будущем, с уверенностью неизвестен. Вместо этого заемщик и кредитор используют свои ожидания будущей инфляции для определения процентной ставки по ссуде. С этой точки зрения мы используем следующую формулу:

сокращенная номинальная процентная ставка ≈ реальная процентная ставка + ожидаемый уровень инфляции.

Мы используем термин контрактная номинальная процентная ставка , чтобы прояснить, что это ставка, установленная во время кредитного соглашения, а не реализованная реальная процентная ставка.

Key Insight

• Чтобы скорректировать номинальную процентную ставку с учетом инфляции, вычтите уровень инфляции из номинальной процентной ставки.

Более формально

Представьте, что два человека подписывают договор о займе в размере P долларов с номинальной процентной ставкой —.Это означает, что в следующем году сумма выплаты составит P × (1 + i ). Это стандартный кредитный договор с номинальной процентной ставкой —.

Теперь представьте, что люди решили подписать договор займа, чтобы гарантировать постоянный реальный доход (в пересчете на товары, а не в долларах), обозначенный р . Таким образом, контракт предусматривает фунтов стерлингов в этом году в обмен на возврат (достаточно долларов для покупки) (1 + рублей ) единиц реального валового внутреннего продукта (реального ВВП) в следующем году.Для погашения этой ссуды заемщик дает кредитору достаточно денег, чтобы купить (1 + r ) единиц реального ВВП на каждую ссужаемую единицу реального ВВП. Таким образом, если уровень инфляции равен π, то уровень цен повысился до P × (1 + π), поэтому выплата в долларах по ссуде в размере P долларов составит P (1 + r ). × (1 + π).

Здесь (1 + π) — единица плюс уровень инфляции. Уровень инфляции π _{t +1} определяется, как обычно, как процентное изменение уровня цен с периода t до периода t + 1.

π _{т +1} = ( P _{т +1} — P _т ) / P _т .

Если период равен одному году, то уровень цен в следующем году равен цене в этом году, умноженной на (1 + π):

P _{т +1} = (1 + π _т ) × P _т .

Уравнение Фишера говорит, что эти два контракта должны быть эквивалентны:

(1 + i ) = (1 + r ) × (1 + π).

В качестве приближения из этого уравнения следует

i ≈ r + π.

Чтобы увидеть это, умножьте правую часть и вычтите 1 с каждой стороны, чтобы получить

i = r + π + r π.

Если r, и π — малые числа, то r π — очень маленькое число, и его можно спокойно игнорировать.Например, если r = 0,02 и π = 0,03, тогда r π = 0,0006, и наше приближение имеет точность около 99 процентов.

Основные области применения этого инструмента

Формула эффекта Фишера | Финансы

Автор: Джеки Лохри | Рецензент: Райан Кокерхэм, CISI Capital Markets and Corporate Finance | Обновлено 5 февраля 2019 г.

Формула «эффекта Фишера» пытается показать, как ожидание инфляции влияет как на процентные ставки, так и на покупательную способность.Эта формула, разработанная в 1930 году экономистом-математиком Ирвином Фишером как часть общей экономической теории, сегодня настолько широко используется в области экономики и финансов, что многие считают ее стилизованным фактом — термином, используемым для описания столь последовательных наблюдений и выводов. они обычно принимаются как истинные. Формула эффекта Фишера не только играет важную роль в научных кругах и бизнесе, но и имеет приложения, которые могут принести пользу вам как инвестору.

Совет

Формула, используемая для расчета эффекта Фишера, требует трех важных параметров данных: номинальной процентной ставки, реальной процентной ставки и ожидаемого уровня инфляции.

Компоненты формулы

Формула эффекта Фишера предполагает период в один год и разбивается на три компонента: номинальная процентная ставка, реальная процентная ставка и ожидаемый уровень инфляции. Номинальная процентная ставка — это процент, показывающий цену, которую вы платите за использование денег, без учета инфляции. Реальная процентная ставка — это процент, который корректируется для устранения влияния инфляции и, как следствие, является мерой «реальной» покупательной способности.Ожидаемый уровень инфляции — это процент, который меняется в зависимости от текущих экономических циклов.

Расчет формулы

Расчет эффекта Фишера не составляет труда. Технический формат формулы: «Rном = Rreal + E [I]» или номинальная процентная ставка = реальная процентная ставка + ожидаемый уровень инфляции. Более простой способ вычислить формулу и определить покупательную способность — разбить уравнение на два этапа. Используйте уравнение «Rnon — E [I] = Rreal», чтобы получить реальный уровень инфляции.Затем определите реальную покупательную способность, скажем, 100 долларов, умножив 100 на Rreal и вычтя сумму из 100. Если Rreal составляет 2 процента, покупательная способность 100 долларов через год будет только 98 долларов.

Краткосрочные применения

Эффект Фишера имеет краткосрочные практические применения, которые вы можете использовать в повседневной жизни. Поскольку это оценка покупательной способности в соответствии с темпами инфляции, вы можете использовать ее для определения «реальной» нормы прибыли на инвестиции с точки зрения того, что ваша прибыль купит.Например, если вы приобретаете 12-месячный депозитный сертификат на 5000 долларов с процентной ставкой 0,94 процента, а инфляция остается постоянной, в конце года у вас будет 5 047,22 доллара.

Однако, если инфляция вырастет на 2 процента в течение года, вы фактически потеряете деньги на вложениях, поскольку ваша прибыль и покупательная способность ваших денег уменьшатся на 53,50 доллара или 1,06 процента, в результате чего вам останется потратить всего 4 993,72 доллара: 2,0 — 0,94 = 1,06 5047,22 * 1,06 = 53,50 5047,22 — 53.50 = 4993,72

Долгосрочное значение

Знание реальной процентной ставки имеет решающее значение для принятия правильных инвестиционных решений. Хотя использование эффекта Фишера для расчета краткосрочных эффектов может оказаться полезным и интересным, результаты становятся еще более значимыми при его применении в долгосрочной перспективе. Сложные расчеты с использованием ваших временных рамок для инвестирования, начальной суммы инвестиций, номинальной процентной ставки и различных темпов инфляции могут быть инструментом для анализа потенциала инвестиций и помочь вам определить, в какой момент экономического цикла имеет смысл продавать.0,5

где,

LPI = Индекс цен Ласпейреса = ∑ (Pn, t) * (Qn, 0) * 100 / (Pn, 0) * (Qn, 0)

PPI = Индекс цен Пааше = ∑ (Pn, t) * (Qn, t) * 100 / (Pn, 0) * (Qn, 0),

где

• Pn, t — цена товара на n ^{-й период}
• Pn, 0 — цена товара в базовом периоде
• Qn, t — количество товара в n ^{-м периоде}
• Qi, 0 — количество товара в базовом периоде

Примеры индекса цен Фишера

Ниже приведены примеры индекса цен Fisher.

Пример # 1

Давайте найдем индекс цен Фишера для трех товаров, цена и количество проданных товаров которых указаны за три года. Для текущего года, обозначенного как Год 0, цены в долларах и количество указаны следующим образом:

	Год 0			Год 1			Год 2
	А	В	С	А	В	С	А	В	С
Цена	20	10	15	22	11	26	24	12	28
Кол-во	15	20	25	20	20	17	25	20	15
Значение	300	200	375	440	220	442	600	240	420

Сначала мы рассчитаем индекс цен Фишера для года 0, используя индекс цен Ласпейреса и индекс цен Пааше. 0.5

= 100

Точно так же мы находим индексы для 1-го и 2-го года, как дано.

за год 1

Индекс цен Ласпейреса

• LPI = (22 * 15 + 11 * 20 + 26 * 25) * 100 / (20 * 15 + 10 * 20 + 15 * 25)
• = 137,14

Индекс цен Пааше

• PPI = (22 * 20 + 11 * 20 + 26 * 17) * 100 / (20 * 15 + 10 * 20 + 15 * 25)
• = 125,94

Индекс Фишера (FPI)

• FPI = (137.0,5
• = 146,27

Мы дали табличное представление индексов в следующей таблице.

Пример # 2

Давайте возьмем случай трех наиболее часто используемых видов топлива: бензина, дизельного топлива и керосина и рассчитаем индексы цен на три года.

Цена в долларах и количество в литрах показаны в следующей таблице.

	Год 0			Год 1			Год 2
	Бензиновый	Дизель	Керосин	Бензиновый	Дизель	Керосин	Бензиновый	Дизель	Керосин
Цена	60	70	50	65	78	52	50	65	45
Кол-во	10	10	15	20	15	18	8	5	10
Значение	600	700	750	1300	1170	936	400	325	450

Мы видим, что цена на топливо увеличилась в 1-м году и снизилась во 2-м году.Вы заметили, что объемы также демонстрируют аналогичную тенденцию, что неудивительно, поскольку мы знаем, что нефтегазовые компании часто сокращают добычу при падении цен на сырую нефть (сырье)?

Таблица, показывающая значения индексов в этом случае, приведена ниже и может быть получена точно так же, как показано в приведенном выше примере.

Преимущества FPI

• FPI часто называют реальным индексом, поскольку он корректирует смещение вверх индекса цен Ласпейреса и смещение индекса цен Пааше в сторону понижения, принимая среднее геометрическое значение двух взвешенных индексов.В качестве веса используются количества как текущего, так и базового года.
• Хотя это не очень часто используемый индекс из-за его структурной сложности и количества требуемых переменных, он очень широко используется в академических кругах и исследованиях.

Недостатки FPI

• Единственное ограничение FPI — это немного более сложные конструкции, чем два других.
• Количество на будущие годы необходимо прогнозировать, в то время как в случае индекса цен Ласпейреса необходимо определять только будущие цены.

Заключение

Хотя индекс Фишера является лучшим из трех индексов, индекс цен Ласпейреса чаще используется для расчетов инфляции. Но если мы можем сделать точный прогноз будущих количеств товара, индекс цен Фишера даст более точную меру.

Рекомендуемые статьи

Это руководство по FPI (Индекс Фишера). Здесь мы обсуждаем формулу и примеры индекса цен Фишера, а также преимущества и недостатки. Подробнее о бухгалтерском учете вы можете узнать из следующих статей —

Домашняя страница Статистического управления / Вопросы и ответы об индексе потребительских цен

Формула Ласпейреса

Ласпейрес предложил эту формулу индекса в 1871 году.В случае расчета индекса цен, предполагая, что для отдельного товара i , цена в базовом периоде будет p _{i 0} , в период наблюдения будет p _it , а количество в базисном периоде должно быть q _{i 0} , следующее уравнение называется «формулой Ласпейреса».

где знаменатель и числитель — это общие расходы по всем статьям в базовом периоде и в период наблюдения, соответственно, при условии, что потребители покупают одинаковое количество товаров как в базовый период, так и в период наблюдения.В этой формуле количества фиксированы в базовом периоде.

Для практического использования уравнение (1) преобразуется следующим образом;

Это средневзвешенное соотношение цен по каждой позиции, взвешенное по расходам в базисном периоде.

Формула Пааше

Пааше предложил эту формулу индекса в 1874 году. В случае расчета индекса цен, предполагая, что для отдельного товара i , цена в базовый период будет p _{i 0} , при наблюдении период будет p _это , а количество в базисном периоде должно быть q _it , следующее уравнение называется «формулой Пааше».

где знаменатель и числитель — это общие расходы по всем статьям в базовом периоде и в период наблюдения, соответственно, при условии, что потребители покупают одинаковое количество товаров как в базовый период, так и в период наблюдения. В этой формуле количества фиксируются на период наблюдения.

Для практического использования уравнение (3) преобразуется следующим образом;

Формула Фишера

Эта формула индекса предложена Фишером и называется «идеальной формулой».Предполагая, что для отдельной позиции i , цены и количество в базисном периоде будут равны p _{i 0} и q _{i 0} , в период наблюдения должен быть p _it and q _it , следующее уравнение называется «формулой Фишера».

Среднее геометрическое по формуле Ласпейреса и Пааше.Обычно выполняется следующее неравенство; Ласпейрес> = Фишер> = Пааше. Формула Фишера называется идеальной формулой в том смысле, что выполняются тест обращения времени и критерий обращения фактора. Эта формула используется в том случае, когда цены и количество на базисе и в период наблюдения сильно различаются.

В Японии базовый период = базисный период цен = базисный период весов.

ФИШЕР (функция) — служба поддержки Office

В этой статье описаны синтаксис формулы и использование функции ФИШЕР в Microsoft Excel.

Описание

Возвращает преобразование Фишера в x. Это преобразование создает функцию, которая обычно распределена, а не искажена. Используйте эту функцию для проверки гипотез о коэффициенте корреляции.

Синтаксис

ФИШЕР (x)

Аргументы функции ФИШЕР следующие:

Замечания

• Если x не является числом, ФИШЕР возвращает # ЗНАЧ! значение ошибки.

• Если x ≤ -1 или x ≥ 1, ФИШЕР возвращает # ЧИСЛО! значение ошибки.

• Уравнение преобразования Фишера:

Пример

Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter.При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.

Формула	Описание	Результат
= ФИШЕР (0,75)	Преобразование Фишера в 0.75	0,9729551

(PDF) Уравнение Фишера: некоторые методологические сомнения

Выручка от продаж 132

Минус стоимость проданных товаров 110

Минус процент 22

—-

Прибыль 0

—-

выплата процентов в размере 22 на раздутый капитал в размере 110 снова составляет ставку 20 процентов

; номинальный и реальный курс равны друг другу и возвращаются к исходному уровню.

Излишне говорить, что продолжающаяся инфляция с неравномерными темпами из года в год или с неравномерными темпами

для разных классов товаров будет держать как производственную систему

, так и финансовую систему в нарушенном состоянии, но это выходит за рамки

.

обсуждение уравнения Фишера.

6. Фридман (1956) был, возможно, первым экономистом, который сделал уравнение Фишера основополагающим строительным блоком макроэкономических моделей

.Но версия, которую продвигает Фридман

[Фридман (1956), уравнение 9] уравнения Фишера:

dt

dp

p

rr

eb

1

+ =

где r

где r

b

— это процентная ставка по облигациям, а

r

e

, реальная ставка Фишера, эквивалентна

норме прибыли, в общем,

собственного капитала

.Но это полная противоположность нашему выводу

в примере из предыдущего раздела, а именно. что это норма операционной прибыли

(включая прибыль по акциям), которая увеличивается с инфляцией по преобладающей номинальной процентной ставке

. Более того, рентабельность собственного капитала является единственной внедоговорной «ценой» в экономике

; все остальные цены, включая процентную ставку, фиксируются в контракте, и

варьируются в зависимости от пересмотра условий контракта, поскольку экономические силы, управляющие их требованиями и поставками

, меняются с течением времени.Рентабельность собственного капитала может стать отрицательной

, иногда

на продолжительные периоды времени. Конечно, он не может соответствовать реальной ставке Фишера

, которая должна быть строго положительной, поскольку она определяется реальными силами

предельной производительности капитала и временным предпочтением текущего потребления над отложенным

. Так что я думаю, что версия уравнения Фишера, представленная Фридманом, — это просто искажение

.Интуитивно гораздо удобнее предположить, что переменная ставка инфляции

влияет, в первую очередь, на переменную неконтрактную рентабельность собственного капитала, при этом

— это временно фиксированная ставка по контракту.

Насколько мне известно, версия уравнения Фридмана

Уравнение Фишера никогда не подвергалась эмпирической проверке. Не нужно быть пророком

, чтобы предсказывать, что если бы он был протестирован с краткосрочными ставками, результаты были бы либо отклонены, либо неубедительны, а если бы оно было проверено с долгосрочными ставками, уравнение

было бы просто отклонено.

3

7. Сказанное не освобождает меня от задачи ответить на два важных вопроса

. Во-первых, почему поведение краткосрочных процентных ставок, кажется, тесно связано

с уравнением Фишера, когда это так? [Например,

см.

Мишкин 2009] Во-вторых, почему

участники рынка, особенно трейдеры рынка денег и облигаций, используют уравнение Фишера

в своей повседневной работе? На мой взгляд, ответ на оба вопроса — один и тот же

.Центральные банкиры используют инструмент процентной ставки для достижения своих краткосрочных целевых показателей инфляции

.