Модель гордона используется для: Модель Гордона. Оценка доходности капитала. Пример расчета в Excel

Модель Гордона.

В продолжении  Дивидендных чемпионов я решил еще раз рассмотреть оценку акции со стороны выплаты дивидендов. В классическом курсе фундаментального анализа (что преподается во всех вузах мира) существует метод оценки акций с равномерно возрастающим дивидендом, который называется моделью Гордона. 

Именно «Дивиденды» можно считать тем самым «купоном» акции, и в России кстати, скептиками фундаментального анализа дивидендам придается большее внимание в расчетах, чем собственному капиталу и чистой прибыли, которая остается в компании.

Дивиденды — это реальный поток наличности акционеру, и если Вы собираетесь держать акцию вечно (как Баффетт), то это будет скорее вложение «как бы в облигацию», а не в акцию, но только на порядок интересней, так как «размер купона будет постоянно расти.

Модель Гордона.

Если начальная величина дивиденда равна 

D, при этом ежегодно увеличивается с темпом прироста g, то формула текущей стоимости сводится к сумме членов бесконечно убывающей геометрической прогрессии:

PV = D*(1+g)/(1+r) + D*(1+g)^2/(1+r)^2 + D*(1+g)^2/(1+r)^2… = D*(1+g)/(r-g)

где PV — текущая стоимость

r — ставка доходности, используемая для дисконтирования будущих поступлений

Попробую проанализировать применение формулы Гордона (для инвестиций именно Баффетта она очень хорошо применима — он владеет акциями вечно) по списку акций из  Дивидендных чемпионов, которые есть на Санкт-Петербургской бирже.

Интересен вопрос, как можно покупать даже «дорогие» компании. Вопрос в качестве бизнеса, бренде, «рве безопасности» — об этом можно много почитать у Баффетта, но как можно всё это перевести в объективные числовые значения?

Во-первых, чтобы компанию вообще можно было посчитать по данной формуле — она должна стабильно выплачивать дивиденды, и они должны расти (соответственно и чистая прибыль, иначе рост дивидендов упрется в показатель чистой прибыли, тут важен уровень EPS% Payout, долги и байбеки компании).

И во-вторых, нужно иметь большую уверенность в продолжение данной ситуации.

Скорее всего это будут компании из потребительского сектора (ввиду большей прогнозируемости фин. результата и темпов роста бизнеса), чем из сырьевого (и других циклических отраслей), где такой стабильности труднее достичь.

Для расчета целевой цены PV использовал значения g – темп прироста дивиденда за последние 5 лет (DGR 5-yr), благо на http://dripinvesting. org/Tools/Tools.htm есть все данные.

А вот с r — ставка доходности, используемая для дисконтирования будущих поступлений, есть проблема. Если отталкиваться от доходности 10Т – около 2,5%, то даже с поправочным коэффициентом х2 – 5% очень мало, и при расчете целевой цены по модели Гордона получаются отрицательные значения. Поставил для расчета условные

r=15%.

Кроме этого на ресурсе http://dripinvesting.org/Tools/Tools.htm есть прогноз дивидендов, я использовал для расчета Целевой цены 2. По средней арифметической двух целевых цен составил рейтинг. Где первая цена была n/a использовал только вторую цену.

Хит-парад акций по модели Гордона

Даже с r=15% получились странные значения. Плюс среднее между прошлым ростом дивидендов и прогнозными значениями внесли еще большую сумятицу.

Чтобы упростить ситуацию, можно пойти с обратной стороны — найти ставку доходности, которую используется для дисконтирования будущих поступлений.

r = (D*(1+g)/PV + g )*100

Я не сильно приветствую оценку компаний на основе методов DCF, ввиду огромной сложности оценки будущих доходов (изменение одного параметра может привести к огромным переменам в оценке), но в данном случае меня заинтересовало, то что можно получить из данной формулы (Гордона) — зная текущую стоимость акции, последний дивиденд за 12 месяцев и темп увеличения дивиденда (взял за последние 5 лет) — можно найти ставку r. 

Получился вот такой список

Конечно, прошлый рост дивидендов – это история, но как информация к сведению — это полезно. Все акции имеют требуемую доходность r значительно выше доходности 10Т (2,4%), это очень хорошо.

Как я писал ранее, присматриваюсь к Verizon, Chevron, ExxonMobil, Wal—

MartStores, Caterpillar, опять же AT&T, и еще интересные идеи в Gilead Sciences, Inc. , Exelon Corporation и Dow Chemical Company.

 

Справочно по теме поста.

АКЦИИ-ОБЛИГАЦИИ С ПОСТОЯННО РАСТУЩИМИ ПРОЦЕНТАМИ ОБЛИГАЦИОННЫХ КУПОНОВ

Уоррен умеет рассматривать инвестиции с разных позиций. Одна из них — это подход к акции как к облигации с постоянно растущим купоном. Давайте исследуем этот вопрос на примере ≪Coca-Cola≫. (Быть может, вы удивляетесь, почему вообще разговор зашел о купонах?
  
В прежние времена облигации выпускались с десятками отрезных купонов. Владелец облигации отрезал купон и высылал его в компанию, выпустившую эту облигацию, получая в ответ проценты, набежавшие за определенный срок. Таким образом, компании не нужно было вести учет всех владельцев облигаций. В наше время облигации регистрируются в компании, выпустившей их, и их держатели получают проценты по почте, ничего для этого не делая. С точки зрения Уоррена, акции-облигации некоторых компаний имеют купоны, выплаты по которым постепенно увеличиваются.

Каждый год вы получаете с этой акции-облигации несколько больше. Вот это и есть акция-облигация с нарастающим купоном.)

Теперь вспомните, о чем мы уже говорили: цена, которую вы платите за акции, предопределяет рентабельность ваших инвестиций. Когда в 1988 г. Уоррен первый раз купил акции ≪Coca-Cola≫, балансовая стоимость одной акции компании равнялась 1,07 доллара, а прибыль на одну акцию составляла 0,36 доллара. Это означает, что рентабельность собственного капитала ≪Coca-Cola≫ в 1988 г. равнялась 33,6%. Если бы вы купили акции ≪Coca-Cola≫ по их балансовой стоимости, т. е. по 1,07 доллара за акцию, первоначальная рентабельность ваших инвестиций составила бы 33,6% (0,36 дол.: 1,07 дол.= 33,6%). Однако Уоррен купил акции не по 1,07 доллара, а по 5,22 доллара, так что первоначальная рентабельность его вложений составила лишь 6,89% (0,36 дол.: 5,22 дол. = 6,89%), т. е. гораздо меньше 33,6%.

Что ж, рентабельность инвестиций в размере 6,89% нельзя назвать большой. Но Уоррен рассчитывал, что прибыли ≪Coca-Cola≫ в расчете на одну акцию будут продолжать расти, что приведет к постепенному повышению среднегодовой рентабельности вложенных им денег.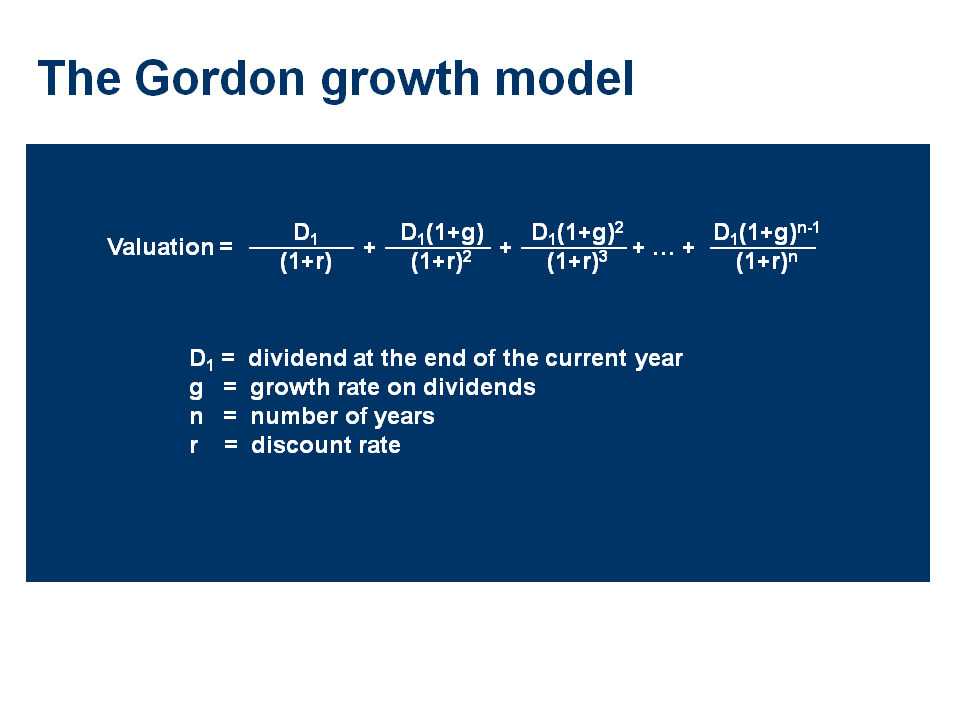 Звучит заманчиво? Давайте изучим этот вопрос подробнее.

Экономическое положение компании ≪Coca-Cola≫ многогранно, но главными показателями являются рентабельность собственного капитала и величина нераспределенной прибыли. В 1988 г. Уоррене каждых 5,22 доллара, вложенных в компанию, заработал 0,36 доллара.

Если ≪Coca-Cola≫ удерживает из этой суммы прибыли примерно 58%, т.е. 0,21 доллара (0,36 дол. х 0,58 = 0,21 дол.), это означает, что она фактически реинвестирует принадлежащие Уоррену 0,21 доллара обратно в компанию. (Отмечу, что оставшиеся 42%, или 0,15 доллара, выплачиваются в виде дивидендов.)

Таким образом, на начало 1989 г. общие вложения Уоррена в компанию ≪Coca-Cola≫ в расчете на одну акцию равняются первоначальным 5,22 доллара плюс нераспределенная прибыль в размере 0,21 доллара, что в сумме дает 5,43 доллара на акцию.

Первоначально вложенный капитал  5,22 дол.

Нераспределенная прибыль за 1988 г. + 0.21 дол.

Суммарный капитал на 1989 г.   5,43 дол.

 
Мы можем предположить, что в 1989 г. первоначально вложенная часть суммарного капитала — те самые 5,22 доллара— снова принесет прибыль в размере 0,36 доллара, т. е. снова увеличится на 6,89%. С другой стороны, если ≪Coca-Cola≫ сохранит прежние темпы роста собственного капитала на уровне 33,6%, то оставшаяся после 1988 г. нераспределенная прибыль в размере 0,21 доллара вырастет на 33,6%, т. е. принесет прибыль в размере 0,07 доллара (0,21 дол. х 0,336 — 0,07 дол.).

 
И значит, общая прибыль на акцию в 1989 г. уже составит 0,43 доллара (0,36 дол. + 0,07 дол. = 0,43 дол.). Итак, Уоррен заработает 0,36 доллара со своего первоначального вложения в размере 5,22 доллара — рентабельность 6,89%, и 0,07 доллара с оставшейся в компании части прибыли в размере 0,21 доллара — рентабельность 33,6%. В сумме это принесет ему 0,43 доллара прибыли на акцию, что соответствует рентабельности суммарного капитала (5,43 дол.) на уровне 7,9% (0,43 дол.: 5,43 дол. = 7,9%).

Прогнозируемая прибыль от инвестированного и реинвестированного капитала и рентабельность инвестиций на 1989 г.

Первоначально вложенный капитал 5,22 дол. х 6,89% = 0,36 дол.

Нераспределенная прибыль за 1988 г. +0.21 дол. х 33,6% =  0,07 дол.

Суммарный капитал на 1989 г. 5,43 дол. 0,43 дол.

Рентабельность инвестиций на 1989 г.:

0,43 дол. (прибыль): 5,43 дол. (капитал) = 7,9%

 
Такие же расчеты можно провести и на 1990 г. Компания ≪Coca-Cola≫ удержит 58% от полученной в 1989 г. прибыли в размере 0,43 доллара, что составляет примерно 0,25 доллара. Эти 0,25 доллара будут добавлены к тем 5,43 доллара, которые Уоррен уже вложил в компанию. Таким образом, его суммарный капитал, вложенный в компанию ≪Coca-Cola≫ (в расчете на одну акцию), составит 5,68 доллара (5,22 дол. + 0,21 дол. + 0,25 дол. = 5,68 дол.).

 
Суммарные инвестиции в 

≪Coca-Cola≫ на начало 1990 г. в расчете на одну акцию:

Первоначально сложенный капитал 5,22 дол.

Нераспределенная прибыль за 1988 и 1989 гг. +0,46 дол.

Суммарный капитал на 1990 г. 5,63 дол.

 
Можно предположить, что в 1990 г. первоначально вложенные Уорреном 5,22 доллара снова принесут прибыль в размере 0,36 доллара, т. е. будут иметь все ту же отдачу на уровне 6,89%. Но зато прибыль, удержанная компанией и добавленная к первоначальному капиталу (0,21 доллара в 1988 г. и 0,25 доллара в 1990 г.), будет нарастать со скоростью, равной текущему уровню рентабельности собственного капитала компании, т. е. 33,6%. Это означает, что нераспределенная в 1988 и 1989 гг. прибыль на акцию в размере 0,46 доллара в 1990 г. принесет прибыль, равную 0,15 доллара (0,46 дол. х 0,336= 0,15 дол.).

Таким образом, общая прибыль на 1990 г. прогнозируется на уровне 0,51 доллара на акцию (0,36 дол. +0,15 дол. = 0,51 дол.). Это соответствует 8,9% общей рентабельности инвестированного и реинвестированного за два года капитала (0,51 дол. :5,68 дол. = 8,9%).

 
Прогнозируемая прибыль от инвестированного к реинвестированного капитала и рентабельность инвестиций на 1990 г.

Первоначально вложенный капитал 5,22 дол. х 6,89% = 0,36 дол.

Нераспределенная прибыль за 1988 и 1989 гг. +0.46 дол, х 33.6% = 0.15 дол.

Суммарный капитал на 1990 г. 5,68 дол. 0,51 дол.

Рентабельность инвестиций на 1990 г. 0,51 дол. (прибыль): 5,68 дол. (капитал) = 8,9%

Уверен, вы заметили поступательный рост нормы доходности, но хочу, чтобы вы обратили внимание на то, что первоначальный капитал Уоррена имеет фиксированную ставку роста 6,89%, зато нераспределенная прибыль, прибавляемая к первоначальному капиталу, растет уже со скоростью 33,6%. На это можно взглянуть и под таким углом: предположим, вы купили акции-облигации ≪Coca-Cola≫ с фиксированной доходностью 6,89%. И каждый раз, получая по почте чек с начисленными процентами, вы покупаете на эти деньги новые акции-облигации ≪Coca-Cola≫, имеющие доходность уже не 6,89, а 33,6%. Вот только чтобы иметь возможность приобретать эти высокодоходные бумаги, сначала вы должны купить акции-облигации с доходностью 6,89%.

Вы платите высокую цену за входной билет, чтобы только переступить порог. Но когда вы уже оказались внутри, на вас проливается золотой дождь. И чем дольше вы остаетесь там, тем обильнее будет этот дождь.

Вот почему Баффетт готов покупать даже «дорогие» компании в «Грехемском» понимании. Я в своих расчетах пытаюсь объединить Грехема и Баффетта (даже несмотря на то, что Баффетт был его учеником, но позже он довольно сильно пересмотрел свою стратегию).

Хорошо бы покупать дешево высокорентабельный бизнес, но с какого-то времени таких компаний не стало (по крайней мере в развитых странах). Я пришел к выводу, что «стратегия Грехема» с запасом прочности лучше работает на развивающих рынках (Россия, Польша, Пакистан и др. ), а «стратегия Баффетта» — покупка «потребительской монополии» за разумную цену на развитых рынках (США, Германия).

Успешных инвестиций!

Модель гордона, формула, расчёт и пример

Модель Гордона — это метод расчета внутренней стоимости акций, исключая текущие рыночные условия. Модель представляет собой метод оценки, предназначенный для определения стоимости акции на основе дивидендов, выплачиваемых акционерам, и темпов роста этих дивидендов. Также её называют: модель роста гордона, модель дисконтирования дивидендов (DDM), модель постоянных темпов роста. Калькулятор здесь.

Модель была названа в честь профессора Майрона Дж. Гордона в 1960-х годах, но Гордон был не единственным финансовым ученым, который популяризировал модель. В 1930-х годах Роберт Ф. Вайз и Джон Берр Уильямс также проделали значительную работу в этой области.

Существует две основные формы модели: стабильная модель и модель многоступенчатого роста.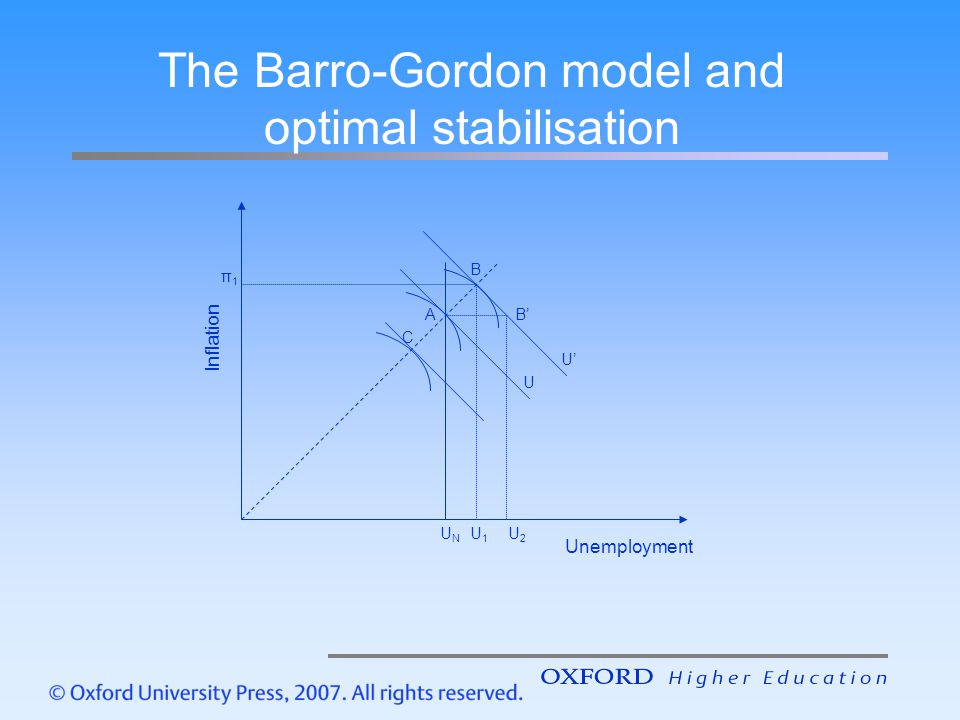

Стабильная модель 

Стоимость акции = D₁ / (k — g) 

где: 

D₁ = ожидаемый годовой дивиденд на акцию в следующем году

g = ожидаемый темп роста дивидендов (обратите внимание — полагается, что он будет постоянен)

Т.е. данная формула позволяет вычислять будущую стоимость акции, через дивиденд, но при условии, что темп роста дивиденда будет одинаков.

Многоступенчатая модель роста 

Если ожидается, что дивиденды не будут расти с постоянной скоростью, инвестор должен оценивать дивиденды за каждый год отдельно, включая ожидаемый темп роста дивидендов за каждый год. Тем не менее, многоступенчатая модель роста предполагает, что рост дивидендов в конечном итоге становится постоянным. Ниже будет пример.

Примеры

Стабильная (устойчивая) модель Гордона

Предположим, компания XYZ намерена выплатить дивиденды в размере 1 долл. США на акцию в следующем году, и вы ожидаете, что в дальнейшем она будет увеличиваться на 5% в год. Предположим также, что требуемая норма прибыли на акции компании XYZ составляет 10%. В настоящее время акции компании XYZ торгуются по 10 долларов за акцию. То есть ещё раз:

— планируется дивиденд 1 доллар на акцию

— дивиденд будет расти на 5% в год

— норма прибыли 10%

— сейчас цена акции 10 долларов

Теперь, используя формулу выше, мы можем рассчитать, что внутренняя стоимость одной акции акций компании XYZ равна:

$1.00 / (0.10 — 0.05) = $20

Таким образом, согласно модели, акции компании XYZ стоят 20 долларов за акцию, но торгуются по 10 долларов; Модель роста Гордона предполагает, что акции недооценены.

Стабильная модель предполагает, что дивиденды растут с постоянной скоростью. Это не всегда реалистичное предположение, потому как дела в компаниях всё же меняются, сегодня у них всё чудесно и они платят хорошие дивиденды, а завтра не платят их вовсе. Поэтому данный способ, со стабильной моделью, когда дивиденд каждый год один и тот же — всё же уступает место многоступенчатой модели роста.

Многоступенчатая модель роста Гордона

Предположим, что в течение следующих нескольких лет дивиденды компании XYZ будут быстро расти, а затем будут расти стабильными темпами. Ожидается, что дивиденды в следующем году по-прежнему составят 1 доллар на акцию, но дивиденды будут увеличиваться ежегодно на 7%, затем на 10%, затем на 12%, а затем увеличиваться на 5% постоянно. Используя элементы устойчивой модели, но анализируя каждый год отдельно, мы можем рассчитать текущую справедливую стоимость акций компании XYZ.

Исходные данные: 

D1 = $1.00 

k = 10% 

g1 (темп роста дивидендов, год 1) = 7%

g2 (темп роста дивидендов, год 2) = 10%

g3 (темп роста дивидендов, год 3) = 12%

gn (темп роста дивидендов в последующие годы) = 5%

Поскольку мы оценили темп роста дивидендов, мы можем рассчитать фактические дивиденды за эти годы: 

D1 = $1. 00

D2 = $1.00 * 1.07 = $1.07 

D3 = $1.07 * 1.10 = $1.18 

D4 = $1.18 * 1.12 = $1.32

Затем рассчитываем приведенную стоимость каждого дивиденда в течение необычного периода роста: 

$1.00 / (1.10) = $0.91 

$1.07 / (1.10)² = $0.88 

$1.18 / (1.10)³ = $0.89 

$1.32 / (1.10)⁴ = $0.90 

Затем мы оцениваем дивиденды, возникающие в период стабильного роста, начиная с расчета дивиденда за пятый год: 

D5 = $1.32 * (1.05) = $1.39

Затем мы применяем формулу модели роста Гордона со стабильным ростом к этим дивидендам, чтобы определить их стоимость на пятый год: 

$1.39 / (0.10-0.05) = $27.80

Приведенная стоимость этих дивидендов за период стабильного роста рассчитывается следующим образом: 

$27.80 / (1.10)⁵ = $17.26

Наконец, мы можем добавить текущую стоимость будущих дивидендов компании XYZ, чтобы получить текущую внутреннюю стоимость акций компании XYZ: 

$0. 91 + $0.88 + $0.89 + $0.90 + $17.26 = $20.84

Многоступенчатая модель роста также указывает на то, что акции компании XYZ недооценены (внутренняя стоимость в 20,84 доллара по сравнению с торговой ценой в 10 долларов).

Аналитики часто включают предполагаемую цену и дату продажи в эти расчеты, если они знают, что не будут удерживать акции бесконечно. Также купонные выплаты могут использоваться вместо дивидендов при анализе облигаций.

Вывод

Модель роста Гордона позволяет инвесторам рассчитать стоимость акций без учета текущих рыночных условий. Это исключение позволяет инвесторам сравнивать компании в различных отраслях, и по этой причине модель Гордона является одним из наиболее широко используемых инструментов анализа и оценки акций. Тем не менее, некоторые относятся к ней скептически.

Математически, чтобы сделать модель Гордона эффективной, необходимы два обстоятельства. Во-первых, компания должна выплачивать дивиденды. Во-вторых, темп роста дивидендов (g) не может превышать требуемую норму прибыли инвестора (k). Если g больше k, результат будет отрицательным, и акции не могут иметь отрицательных значений.

Модель Гордона, особенно многоступенчатая модель роста, часто требует от пользователей делать несколько нереалистичных и сложных оценок темпов роста дивидендов (g). Важно понимать, что модель чувствительна к изменениям g и k, и многие аналитики проводят анализ чувствительности, чтобы оценить, как различные предположения меняют оценку. В соответствии с моделью Гордона, акции становятся более ценными, когда их дивиденды увеличиваются, требуемая норма прибыли инвестора уменьшается, или ожидаемая скорость роста дивидендов увеличивается. Модель роста Гордона также подразумевает, что цена акций растет с той же скоростью, что и дивиденды.

Модель Гордона: формула, пример расчета

В сфере инвестирования есть довольно много различных способов, чтобы просчитать экономические эффекты. Некоторые из них относятся к государственным облигациям, другие исследуют различные аспекты деятельности разных компаний, определяя их привлекательность. Третьи предлагаются как способ реалистической оценки стоимости активов. Конечно, есть ещё целый ряд дополнительных параметров, которые можно сюда добавить, но об этом как-то потом. Сейчас в рамках статьи наибольший интерес представляет вопрос: что такое модель Гордона? Используется для чего? Что моделирует, какой результат показывает и как его толковать? По каким формулам считается?

Что называют моделью Гордона?

Модель Гордона – это вариация модели дисконтирования дивидендов, которая используется, чтобы вычислять цену акции или бизнеса. Свое основное применение она нашла в вычислении стоимости компаний, которые не котируются на биржах и которые сложно оценить другим экономическим инструментарием. Также можно встретить расширенное название – модель роста Гордона.

Какая формула?

А как, собственно, смоделировать какую-то ситуацию? Довольно просто – с помощью математики. Следует отметить, что модели Гордона могут быть созданы под множество ситуаций, которые, соответственно, будут влиять на содержание формулы. Но чтобы у вас было представление, о чем будет вестись речь, предлагают разобрать довольно популярное уравнение, созданное для дивидендных выплат, которые будут в следующем году с условием увеличения их на размер среднего темпа роста. Итак, модель Гордона, формула:

• ДСК = (ДВТП х (1 + СТРД)) : САТМ + СТРД.

Расшифровка сокращений такая:

1. ДСК – доходность собственного капитала у компании.
2. ДВТП – дивидендные выплаты текущего периода.
3. СТРД – средний темп роста дивидендов.
4. САТМ – стоимость акции на текущий момент, которую оценивает модель Гордона.

Пример расчета

Моделирование вручную довольно проблематичное и требует много времени. Поэтому массово используются вспомогательные среды, такие как Excel. Предположим, что одна акция «Газпром» стоит 150,4 рубля. Вы можете видеть пример расчета ниже. Формулы, по которым считалось:

1. Ожидаемая доходность акции = B20 х (1 + D7) : E7 + D7.
2. Среднегодовой темп роста дивидендов = (B20 : B7) ^ (1 : 13) — 1.

Зачем она необходима?

Моделью Гордона могут воспользоваться, чтобы обеспечить разработку трудной оценки, при проведении налогового планирования, а также во время оценивания акции, имеющей равномерный рост дивиденда на фондовом рынке. Также применение является эффективным в таких случаях:

1. Увеличение объема рынка сбыта.
2. Имеются стабильные поставки сырья и материальных ресурсов, необходимых для производства.
3. Применяемые технологии и оборудование высокоэффективны, и их замена не предвидится в ближайшие несколько лет, или существуют гарантии, что будет проведена модернизация по самому последнему слову техники в ближайшее время.
4. У предприятия есть денежные ресурсы, которые могут быть направлены на его усовершенствование.
5. Наблюдается стабильная экономическая ситуация.

Следует сообщить, что прогноз дивидендов сам по себе является чрезвычайно сложной задачей из-за существования различных хозяйственных рисков (которые имеются всегда, даже если перед этим предприятие оценивалось и получило хорошие отклики относительно стабильности бизнеса). Так, существует довольно много методов оценки размера выплат, которые ставили своей целью сделать всё как можно точнее. Также накладываются определённые ограничения. Так, модель Гордона используется на основании, что будет существовать стабильный темп прироста дивидендных выплат. К слову, данный сегмент экономики настолько специфичен, что его оценка иными методами не представляется возможной.

Особенность данной модели

Какие же особенности может предоставить данная модель? Главное и самое интересное заключается в том, что если соблюдаются определённые условия, то уравнение становится полноценным эквивалентом общей формулы дисконтирования потока денежных единиц. Так, чтобы определить бизнесу текущую стоимость собственного капитала, необходимо, чтобы все ожидаемые денежные потоки интересующего периода были разделены на разницу, которая возникает между ставкой дисконтирования и темпом прироста. Тут следует сообщить, что сначала Гордон искал решение, чтобы вычислить прибыль, на которую можно рассчитывать. Поэтому сначала данные расчеты назывались «моделью дивидендов». Но, несмотря ни на что, уравнение, приведенное здесь, является довольно общим.

Кстати, разница между ставкой дисконтирования и темпом прироста считается нормой капитализации. Можно ещё подсчитать множитель (или коэффициент) дохода. Для этого необходимо единицу поделить на норму капитализации. Поэтому сложно не согласиться с утверждением, что уравнение Гордона совместимо ещё и с общей моделью оценки. Чтобы математически определить привлекательность бизнеса, доходы производятся на коэффициент. Благодаря этому свойству, при обращении к модели Гордона становится легче делать анализ информации о запасах или состоянии всего предприятия/компании. Применяться расчеты, полученные с помощью таких формул, могут, чтобы эффективно управлять бизнесом или для оценки его стоимости. Также в экономической литературе можно иногда встретить такой термин, как «модель РОСТА».

Ограничения использования

Следует отметить, что при всех своих преимуществах модель Гордона имеет довольно ограниченную сферу использования. Так, совершать расчеты по ней могут только те компании, которые на данный момент имеют стабильные темпы роста. Чтобы корректно использовать полученную информацию, данные для определения темпа роста должны пройти тщательный отбор.

Идеально подпадают под модель Гордона те компании, которые могут похвастаться своим ростом, который равен номинальному увеличению экономики (или имеют темп прироста меньше него). При этом необходимо иметь четкую и сформулированную политику, которая относится к выплатам дивидендов и которая будет проводиться в будущем.

Заключение

В заключение можно вывести важность, которую предоставляет данный экономический инструментарий. Следует помнить, что он позволяет оценивать предприятия и компании, которые не находятся на биржах.

Также довольно важным является его роль для установления текущего состояния в организации, а также планирования уровня доходности, который ожидается в ближайшее время. Также обязательно учитывать реалии, в которых вы будете всё использовать. Здесь представлено несколько формул для разных случаев, и если вас интересует данная тема – они будут полезными в освоении экономических дисциплин в рамках университета или самообразования.

Wikizero — Модель Гордона

Модель Гордона является вариацией модели дисконтирования дивидендов, методом для вычисления цены акции или бизнеса. Данная модель часто используется для оценки стоимости внебиржевых компаний, которую сложно оценить другими методами.

Модель подразумевает, что компания на сегодняшний день выплачивает дивиденды в размере D, которые в будущем будут увеличиваться с неизменной ставкой g. Также подразумевается, что требуемая процентная ставка (ставка дисконтирования) акции остается постоянной на уровне k.

Тогда текущая стоимость акции будет равна:

P=D∗1+gk−g{\displaystyle P=D*{\frac {1+g}{k-g}}}.

На практике P часто корректируется с учётом различных факторов, например, размера компании. Распространено использование упрощенного вида формулы

P0=D1k−g{\displaystyle P_{0}={\frac {D_{1}}{k-g}}}

где D1{\displaystyle D_{1}} — дивиденд будущего года D1=D0(1+g){\displaystyle D_{1}=D_{0}(1+g)}. {t-1}}{1-{\frac {1+g}{1+k}}}}}.

Тогда, учитывая что t→∞{\displaystyle t\rightarrow \infty } и g<k{\displaystyle g<k}:

P=D∗1+g1+k∗11−1+g1+k=D∗1+g1+k∗1k−g1+k{\displaystyle P=D*{\frac {1+g}{1+k}}*{\frac {1}{1-{\frac {1+g}{1+k}}}}=D*{\frac {1+g}{1+k}}*{\frac {1}{\frac {k-g}{1+k}}}}.

В результате получим:

P=D∗1+g1+k∗1+kk−g=D∗1+gk−g{\displaystyle P=D*{\frac {1+g}{1+k}}*{\frac {1+k}{k-g}}=D*{\frac {1+g}{k-g}}}

Доход плюс прирост капитала равно общей доходности[править | править код]

Модель дисконтирования дивидендов может также быть использована для утверждения, что общая норма доходности акции равна сумме ее дохода и прироста капитала.

D1k−g=P0{\displaystyle {\frac {D_{1}}{k-g}}=P_{0}} может быть преобразована в D1P0+g=k{\displaystyle {\frac {D_{1}}{P_{0}}}+g=k}

Дивидендная доходность (D1/P0){\displaystyle (D_{1}/P_{0})} плюс рост (g) равны стоимости собственного капитала (k)

Предположим, что темп роста дивидендов в модели является прокси-переменной роста доходов и в целом цены акции и прироста капитала. Также предположим, что стоимость собственного капитала есть прокси-переменная требуемой нормы доходности инвесторов.^[1]

Доход+Прирост капитала=Общая доходность{\displaystyle {\text{Доход}}+{\text{Прирост капитала}}={\text{Общая доходность}}}

Темп роста не может превышать норму доходности собственного капитала[править | править код]

Из первого уравнения можно заметить, что k−g{\displaystyle k-g} не может быть отрицательной. Когда в краткосрочном периоде темп роста дивидендов превышает стоимость собственного капитала (норму доходности собственного капитала), то обычно используют двухступенчатый метод модели:

P=∑t=1ND0(1+g)t(1+k)t+P

Гордона модель — это… Что такое Гордона модель?



Гордона модель

Гордона модель (Gordon’s model) -предложенное экономистом М. Дж.Гордоном  упрощенное уравнение, при определенных условиях эквивалентное общему уравнению дисконтирования денежного потока:

V₀ = CF₁/(r – g),  где

V₀ = приведенная (текущая) стоимость собственного капитала бизнеса
CF₁  = ожидаемый денежный поток (или доход) для периода 1
r = ставка дисконтирования
g = темп прироста
Модель Гордона первое время была предназначена для дивидендов, поэтому ее называли  Гордона моделью дивидендов. Однако уравнение  получилось более общим. Выражение (r – g) известно как норма капитализации, а выражение 1/(r –g) это множитель  (коэффициент) к доходу. Таким образом, модель Гордона совместима с общей моделью оценки:

Стоимость = Доходы , помноженные на некий множитель (коэффициент)

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

• Гомори способ
• Горизонт планирования

Смотреть что такое «Гордона модель» в других словарях:

• Гордона модель — Предложенное экономистом М. Дж. Гордоном упрощенное уравнение, при определенных условиях эквивалентное общему уравнению дисконтирования денежного потока: V0 = CF1/(r – g), где V0 = приведенная (текущая) стоимость собственного капитала бизнеса CF1 …   Справочник технического переводчика

• Модель Гордона — является вариацией модели дисконтирования дивидендов, методом для вычисления цены акции или бизнеса. Данная модель часто используется для оценки стоимости внебиржевых компаний, которую сложно оценить другими методами. Модель подразумевает, что… …   Википедия

• Модель постоянного роста — модель дисконтирования дивиденда, предполагающая фиксированную ставку роста будущих дивидендов и единую ставку дисконтирования. По английски: Constant growth model Синонимы: Модель Гордона Шапиро См. также: Модели дисконтирования дивидендов… …   Финансовый словарь

• Модель постоянного роста — Также называется моделью Гордона Шапиро. Применение модели дивидендного дисконта, которая учитывает (1) фиксированную ставку роста будущих дивидендов и (2) единую ставку дисконтирования …   Инвестиционный словарь

• Уравнение синус-Гордона — Уравнение синус Гордона  это нелинейное гиперболическое уравнение в частных производных в 1 + 1 измерениях, включающее в себя оператор Даламбера и синус неизвестной функции. Изначально оно было рассмотрено в XIX веке в связи с… …   Википедия

• Двухстадийная модель дисконтирования денежного потока — (two stage DCF model) в теории оценки бизнеса — основная модель метода дисконтирования денежного потока (ДДП), содержит следующие два последовательных этапа, подразделяющих прогнозный денежный поток на два разряда: 1) промежуточные денежные …   Экономико-математический словарь

• двухстадийная модель дисконтирования денежного потока — В теории оценки бизнеса основная модель метода дисконтирования денежного потока (ДДП), содержит следующие два последовательных этапа, подразделяющих прогнозный денежный поток на два разряда: 1) промежуточные денежные потоки (для конечного… …   Справочник технического переводчика

• СИНУС-ГОРДОНА УРАВНЕНИЕ — релятивистски инвариантное ур ние …   Физическая энциклопедия

• ОПТИЧЕСКАЯ МОДЕЛЬ ЯДРА — полуфеноменологич …   Физическая энциклопедия

• Финансовое моделирование — (financial modeling) применение математических моделей  (формул) для решения задач финансовой математики в разных областях, в том  числе в банковском деле, в области оценки бизнеса и др.. Основные задачи финансовой математики –расчет, анализ и… …   Экономико-математический словарь

Оценка в условиях неопределенности Часть 3[1]

Когда я написал первый блог на эту тему, я думал, что он будет единственным. Сейчас, мне представляется, что данная тема еще долго будет оставаться актуальной! Мой опыт проведения оценок рыночной стоимости недвижимости в России в последние несколько лет выявил ряд проблем при определении стоимости в ситуации, когда рынок существует в условиях неопределенности в лучшем случае, а в худшем – попросту отсутствует! В данной публикации освещается ряд вопросов, относящихся к технике выполнения оценок и возможные подходы к их решению.

В условиях неопределенности возрастает важность независимых оценок стоимости. Они способны придать уверенность и обеспечить поддержку инвесторам, банкам и акционерам для продолжения работы на рынках капитала. Тем не менее бывает очень трудно прийти к надежным заключениям и отстаивать их перед сторонами, которые часто и совершенно правомерно имеют разные интересы. Конечно, в данной ситуации может возникнуть соблазн исходить из худшего прогноза, однако, это редко помогает, на мой взгляд. Гораздо продуктивнее попытаться понять все стороны, участвующие в игре.

Хотел бы предупредить, данный блог не похож на мои предыдущие двухстраничные блоги, в которых я рассматриваю вопросы в краткой и развлекательной манере… тех, кто рискнет продолжить читать дальше, ждет довольно много технического анализа, который обязательно требует разъяснения деталей, хотя я старался не прибегать к профессиональным терминам. Те, кто предпочтет краткую версию, могут сразу перейти в конец блога в раздел, начинающийся со слов: «Если вы не читали текст выше».

Итак, начнем сначала… Рыночная стоимость в соответствии с Международными Стандартами Оценки^[2] (МСО 104, раздел 30.1 имеет следующее определение: «Рыночная стоимость — это предполагаемая (estimated) денежная сумма, за которую состоялся бы обмен актива или обязательства на дату оценки между заинтересованным покупателем и заинтересованным продавцом в результате коммерческой сделки после проведения надлежащего маркетинга, при которой каждая из сторон действовала бы, будучи хорошо осведомленной, расчетливо и без принуждения». Данное определение вызывает ряд вопросов при проведении оценок в условиях неопределенности:

1. В первую очередь, следует уточнить, что такое «предполагаемая денежная сумма». Рыночная стоимость, приведенная в отчете – это всегда мнение оценщика, основанное на фактах, относящихся

моделей спагетти урагана Гордон: где Гордон выйдет на берег в Миссисипи СЕГОДНЯ ВЕЧЕРОМ? | Мир | News

Нынешний ветер со скоростью 65 миль в час обрушивается на побережье Мексиканского залива недалеко от юго-западных штатов после вчерашнего удара по южной оконечности Флориды.

Центр Гордона находился в 145 милях (235 км) к востоку-юго-востоку от устья реки Миссисипи по состоянию на 16:00 BST сегодня днем ​​(10:00 CDT), согласно Национальному управлению океанических и атмосферных исследований (NOAA).

Последнее предупреждение NOAA гласит: «Внешние железнодорожные полосы создают шквалистую погоду вдоль побережья Западной Флориды Панхандл.

«Гордон ожидал, что сегодня ночью ураган выйдет на берег».

Шторм движется со скоростью 15 миль в час.

Где Гордон выйдет на берег в Миссисипи сегодня вечером?

Ожидается, что «Гордон» столкнется с границей между Луизианой и Миссисипи, когда он впервые приземлится сегодня вечером.

Предупреждение об урагане было выпущено для Миссисипи, Луизианы и Алабамы, во всех трех штатах объявлено чрезвычайное положение.

По мере того, как Гордон выходит на берег, ожидается, что он продолжит движение по северо-западной траектории, согласно последним моделям спагетти от Cycloncane.com.

Путь шторма, скорее всего, пойдет на север через Джексон и Виксбург в Миссисипи, а затем перейдет в некоторые части Луизианы, а затем на Арканзас.

По заявлению правительственных чиновников, ожидается, что ветер на уровне урагана принесет в Луизиану и Миссисипи 8 дюймов дождя.

Предупреждение о штормовом нагоне, означающем, что существует также угроза для жизни, действует для Shell Beach, расположенного недалеко от Нового Орлеана, до острова Дофин.

Агентство по чрезвычайным ситуациям штата Миссисипи готовится открыть убежище в 19:00. BST (13:00 по местному времени).

Власти написали в Твиттере: «Государственный приют для медицинских нужд по адресу 1640 Coy Ave в Виггинсе откроется сегодня в 13:00 в ответ на #TropicalStormGordon.

«Это учреждение является убежищем последней инстанции для тех людей, чьи медицинские потребности не могут быть удовлетворены в обычном приюте для населения».

Людей предупредили об эвакуации в случае необходимости и запасе воды, продуктов питания и припасов на три дня, а также средств связи, таких как телефоны.

А как насчет Луизианы?

Волны начали обрушиваться на части побережья Мексиканского залива США, и люди делятся в социальных сетях изображениями больших волн и густых серых облаков неба.

Губернатор Луизианы Джон Бел Эдвардс заявил, что 200 военнослужащих Национальной гвардии были переброшены на юго-восток Луизианы после объявления чрезвычайного положения в штате ранее.

Он сообщил, что 63 грузовика с большой водой, 39 лодок и четыре вертолета также были отправлены вперед для подготовки к приходу шторма.

Рабочие двух морских нефтяных платформ в Мексиканском заливе были эвакуированы в понедельник.

В море добывается 17 процентов сырой нефти и 5 процентов суточной добычи природного газа.

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследование
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О MIT
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О MIT

Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

PPT — Объясняет ли модель Барро-Гордона поведение инфляции в Румынии? PowerPoint Presentation

Академия экономических исследований Докторская школа финансов и банковского дела Объясняет ли модель Барро-Гордона поведение инфляции в Румынии? Магистр: Ана Алексе Научный руководитель: профессор Моисэ Алтэр Бухарест, июль 2008 г.

Темы • Введение • Обзор литературы • Модель временной согласованности Баррогордона • Исходные данные • Оценка естественного уровня безработицы • Оценка инфляции и безработицы в соответствии с Модель Барро-Гордона • Тесты модульного корня • Тесты коинтеграции • Выводы

1.Введение • Существует много ситуаций, в которых один экономический агент (например, правительство) имеет стимул обмануть другого экономического агента. • Интуитивно политики, стремящиеся приблизить уровень безработицы к естественному уровню, испытывают соблазн сделать это, создав неожиданную инфляцию. Домохозяйства, будучи рациональными агентами, прекрасно предвидят соблазн раздувать и соответствующим образом корректировать свои решения. В результате результатом равновесия является ситуация без снижения безработицы и более высокой инфляции, чем раньше (результат «смещения инфляции»).• Целью данной статьи является анализ проблемы несогласованности во времени между рядами уровней инфляции и безработицы для Румынии с использованием тестов на единичный корень и тестов совместной интеграции, фильтра Ходрика-Прескотта и фильтра Калмана в качестве методов оценки, чтобы проверить результат Барро. — Значение модели Гродона.

2. Обзор литературы • В литературе известны различные типы несогласованности во времени: • несогласованность во времени из-за изменений предпочтений с течением времени (Strotz (1956)) • несогласованность во времени планов правительства, когда агенты иметь рациональные ожидания (Лукас (1976), Кидланд и Прескотт (1977), Барро и Гордон (1983)).• Идея о том, что правильная структура денежно-кредитной политики имеет решающее значение для достижения хороших показателей инфляции, была впервые предложена Кидландом и Прескоттом (1977). Ключевой результат состоит в том, что, если политики не могут взять на себя обязательства в отношении будущей политики, темпы инфляции выше, чем если бы они могли взять на себя обязательства. • Барро и Гордон (1983) развили эту идею. Они утверждают, что существует оптимальный механизм наказания и что никакого вмешательства не требуется. • Ирландия (1999) первоначально провела тесты временных рядов для Соединенных Штатов на основе модифицированной модели Барро-Гордона.Он показывает, что модель согласованной во времени денежно-кредитной политики Барро и Гордона (1983) налагает долгосрочные ограничения на свойства временных рядов инфляции и безработицы, которые не отвергаются данными в США.

3. Модель временной согласованности Барро-Гордона • Допущение модели BG: • инфляция положительно зависит от уровня естественной безработицы • инфляция унаследует устойчивость естественного уровня безработицы, когда центральный банк не может проводить денежно-кредитную политику правило • Ирландия (1999): • фактический уровень безработицы нестационарен • ошибки контроля инфляции — что позволяет модели учитывать временные отклонения между фактическим уровнем безработицы и естественным уровнем

3.Модель согласованности во времени Барро-Гордона • Уравнения модели • Кривая Филлипса ожиданий (1) • естественный уровень (2) • фактический уровень инфляции (3) • минимизация функции потерь, которая штрафует отклонения безработицы и инфляции от целевых значений : k * Unt и 0 • (1) и (3) => проблема лица, определяющего политику, принимает следующий вид:

3. Модель согласованности времени Барро-Гордона • Решение модели • условие первого порядка (4) • в равновесии • при использовании (4) => (5) инфляционная погрешность, возникающая из-за неспособности политика принять обязательства, положительно зависит от ожидаемой естественной ставки • из (1), (3) и (5) => (6), что показывает как ошибка управления инфляцией (ηt) позволяет фактическому уровню безработицы в равновесии колебаться вокруг естественного уровня

3.Модель согласованности времени Барро-Гордона • Решение модели • объединение (6) и (2) => (7) • объединение (2), (3) и (5) => (8) • по отдельности, (7 ) и (8) указывают на то, что и инфляция, и безработица нестационарны, наследуя единичные корни от естественного уровня безработицы • вместе они подразумевают, что линейная комбинация инфляции и безработицы является стационарной (9) • Уравнение (9) суммирует ограничение, которое теория Барро и Гордона налагает на долгосрочное поведение инфляции и безработицы: согласно модели, эти переменные должны быть нестационарными, но совместно интегрированными.

4. Входные данные Связь между двумя переменными положительна, что означает, что дополнительный процент безработицы на один процентный пункт увеличивает уровень инфляции.

5. Оценка естественного уровня безработицы • Недостатком этого представления является то, что оно включает ненаблюдаемый естественный уровень безработицы и отсутствуют прямые измерения естественного уровня безработицы. • Статистические подходы к оценке меняющегося во времени естественного уровня безработицы: • Фильтр Ходрика Прескотта — широко используется макроэкономистами для получения гладкой оценки компонента долгосрочного тренда ряда • Фильтр Калмана — наиболее часто используемый метод фильтрации сокращенной формы для оценка естественного уровня безработицы благодаря простоте его оценки

5.Оценки естественного уровня безработицы • Фильтр Ходрика-Прескотта (HP) • Фильтр HP — двусторонний линейный фильтр, который вычисляет сглаженный ряд s y путем минимизации дисперсии y вокруг s с учетом параметра штрафа • Штраф Параметр управляет гладкостью ряда (λ = 14.400 для ежемесячных данных). • Оцениваемая здесь тенденция учитывает естественный уровень безработицы.

5. Оценки естественного уровня безработицы • Фильтр Калмана • Я использую фильтр Калмана Калмана (1960) и Калмана и Бьюси (1961), поскольку он имеет главное преимущество, позволяя использовать изменяющийся во времени естественный коэффициент безработицы оценивается совместно с кривой Филлипса.• Общая спецификация: • Уравнение (1) представляет собой кривую Филлипса — оно моделирует неожиданную инфляцию как функцию: шоков (xt) и разрыва безработицы (Ut — Unt) • Естественный уровень безработицы (Unt) изменяется во времени и его движение моделируется уравнением (2) • Прогнозы, полученные методом экспоненциального сглаживания, используются для отслеживания сезонных движений в фактических рядах, поскольку он дает хорошие результаты

5. Оценки естественного уровня безработицы • Hodric- Фильтр Прескотта по сравнению с фильтром Калмана • Ключевое различие между фильтром HP и фильтром Калмана состоит в том, что оценки естественного уровня безработицы фильтра HP более тесно связаны с фактическим уровнем безработицы => размер разрыва в безработице меньше, чем оценки, основанные на фильтр Калмана.

5. Оценки естественного уровня безработицы • Тесты единичного корня для расчетного естественного уровня безработицы

6. Оценки инфляции и безработицы согласно модели Барро-Гордон Уравнения (7) и (8 ) показывают, что согласно модели и инфляция, и уровень безработицы должны быть единичными корневыми процессами. • Тесты единичного корня для инфляции — случай фильтра HP => πt = 0.1343 * Unt-1 + 5,6319 * ΔUnt-1 + ηt (15.54) (6.08) • Из таблицы выше видно, что инфляция, определяемая BG, имеет единичный корень, который соответствует модели. • * Критические точки 1%, 5% и 10% уровней значимости: 1,98, 2,63, 3,39

6. Оценка инфляции и безработицы в соответствии с моделью Барро-Гордона • Тесты единичного корня для инфляции — случай фильтра Калмана => πt = 0.0885 * Unt-1 -0.0344 * ΔUnt-1 + ηt (17.31) (-3.81) • Из приведенной выше таблицы видно, что инфляция, определяемая BG, имеет единичный корень, который соответствует модели.

6. Оценка инфляции и безработицы в соответствии с моделью Барро-Гордона • Тесты единичного корня для безработицы — случай фильтра HP => Ut = Unt-1 + 1,7344 * (Unt-1- Unt-2) + εt ( 2.62) • Из таблицы выше видно, что уровень безработицы, определяемый BG, имеет единичный корень, который соответствует модели.

6. Оценка инфляции и безработицы в соответствии с моделью Барро-Гордона • Тесты единичного корня для безработицы — случай фильтра Калмана => Ut = Unt-1 -3,2745 * (Unt-1- Unt-2) + εt ( -3.006) • В заключение, мы не можем сказать, соответствует ли уровень безработицы гипотезе модели о том, что безработица является нестационарной, если естественный уровень безработицы нестационарен.

7. Тесты на единичный корень • Результаты тестов на единичный корень • В случае, когда естественный уровень безработицы определяется фильтром Ходрика Прескотта, и инфляция, и безработица кажутся процессами единичного корня, что согласуется с выводом модели . • В случае, когда естественный уровень безработицы определяется с помощью фильтра Калмана, инфляция является процессом с единичным корнем, но трудно сказать, является ли безработица стационарной или нестационарной, поэтому мы не можем сказать, соответствует ли этот случай или нет с моделью Барро-Гордона.

8. Коинтеграционные тесты • Уравнение (9) подразумевает, что линейная комбинация уровня безработицы и инфляции является стационарной, даже если эти две переменные нестационарны независимо друг от друга. • Тест совместной интеграции Филлипса-Улиариса (PO) • Проверяемая гипотеза — H0 — отсутствие совместной интеграции между инфляцией и уровнем безработицы

8. Тесты совместной интеграции • Тест совместной интеграции Филлипса-Улиариса (PO) • HP Случай фильтра: t-статистика> критические значения * при 1%, 2.Уровни значимости 5% и 5%, мы отвергаем H0: нет совместной интеграции между инфляцией и уровнем безработицы, что означает, что данные, по-видимому, согласуются с выводом модели Барро-Гордона о том, что инфляция и безработица взаимосвязаны, согласно тест совместной интеграции ПО. • Случай фильтра Калмана: t-статистика << критические значения на уровнях значимости 1%, 2,5% и 5%, в этом случае мы не можем отклонить H0: отсутствие совместной интеграции между инфляцией и уровнем безработицы, что означает, что линейное сочетание инфляции и уровня безработицы нестационарно.* t - критические значения при 1%, 2,5% и 5% равны -3,39, -3,05 и -2,76 соответственно

8. Тесты коинтеграции • Метод Энгла Грейнджера (EG) • Этот метод включает оценку долгосрочного периода Уравнение (9) с помощью стандартного метода регрессии, а затем остатки восстанавливаются и проверяются на стационарность с применением тестов ADF и PP.

8. Тесты коинтеграции • Тест соинтеграции Йохансена • В приведенном ниже анализе предполагается, что в отношении коинтеграции нет константы (как подразумевается в модели BG) и что нет детерминированных тенденций в данных ; при этом предположении в предварительную регрессию не включаются никакие постоянные члены.• Необходимо учитывать две статистические данные; след и максимальное собственное значение. • Учитывая, что для обоих тестов статистика теста превышает свое критическое значение (5%), когда нуль равен r = 0, мы можем заключить, что присутствует по крайней мере один вектор совместной интеграции. • Для более чем одного вектора совместной интеграции тестовая статистика меньше критического значения, поэтому мы заключаем, что присутствует только один вектор совместной интеграции. • Коинтегрирующий вектор: πt = 0,085486 * ut

8. Тесты коинтеграции • Тест совместной интеграции Йохансена • Учитывая, что для обоих тестов статистика теста меньше своего критического значения (5%), когда нуль равно r = 0, можно сделать вывод, что вектор коинтеграции отсутствует.

8. Тесты коинтеграции • Тест совместной интеграции Йохансена • Согласно статистике максимального собственного значения, существует только 1 вектор совместной интеграции. Мы вычисляем отношение правдоподобия: • Проверенная гипотеза: H0 — нет совместной интеграции между инфляцией и уровнем безработицы. • Поскольку рассчитанное отношение правдоподобия = 10,2418 <критические значения правдоподобия на уровнях значимости 1%, 2,5% и 5%, мы не можем отклонить H0: отсутствие совместной интеграции между инфляцией и уровнем безработицы. * Критические значения вероятности 1%, 2.5% и 5% составляют 15,69, 13,27 и 11,44 соответственно.

8. Тесты коинтеграции • Результаты тестов коинтеграции • Векторы совместной интеграции, определенные с помощью трех тестов совместной интеграции, аналогичны. • В качестве заключения: • Могу сказать, что значение коинтеграции модели Барро-Гордона может быть доказано только в том случае, когда естественный уровень безработицы оценивается с использованием фильтра Ходрика-Прескотта. • В другом случае, когда естественный уровень безработицы оценивается с помощью фильтра Калмана, последствия коинтеграции не могут быть доказаны, главным образом потому, что мы не смогли доказать, является ли уровень безработицы нестационарным или нет.

8. Выводы • Модель предполагает, что процессы инфляции и уровня безработицы зависят от эволюции естественного уровня безработицы • При предположении, что естественный уровень безработицы следует единичному корневому процессу, инфляции и уровню безработицы должны быть нестационарными, в то время как в долгосрочной перспективе эти две переменные интегрируются совместно.

8. Выводы • Глядя на представленные результаты и анализируя последствия модели Барро-Гордона, я прихожу к выводу, что: • инфляция и безработица являются единичными корневыми процессами, что соответствует модели: как инфляция, так и безработица нестационарна в обоих случаях, представленных для оценки естественного уровня безработицы • Я смог доказать, что две переменные совместно интегрированы, только в том случае, когда я произвел оценку естественного уровня безработицы с использованием фильтра Ходрика Прескотта — это соответствует значению модели для совместной интеграции • Результаты в этом документе поддерживают модель Барро-Гордона для объяснения долгосрочного поведения инфляции в Румынии.

No related posts.