Сложные проценты с ежемесячным внесением платежа
Выполняем просьбу пользователя frouzen, который просил написать Финансовый калькулятор. — рассчитывающий наращенную сумму при использовании сложных процентов и довложении средств ежемесячно равными платежами. Начисление процентов предполагается тоже ежемесячное (самый выгодный случай).
Чтобы не отвлекать пользователя от калькулятора, ниже идет сам калькулятор, а немного теории и формул надо смотреть под ним, кому не лень.
Калькулятор
Сложные проценты с ежемесячным вложением равной суммы
Точность вычисленияЗнаков после запятой: 2
Наращенная сумма
save Сохранить share Поделиться extension Виджет
Формула сложных процентов, начисляемых несколько раз в течении года
, где m в нашем случае равно 12, а n — срок вклада в годах
Это простейший случай при внесении вклада сразу, и без дальнейшего его пополнения.
Теперь займемся более сложным случаем — пополнением вклада одинаковыми платежами ежемесячно.
Заметим, что множитель степени mn
Таким образом, для самого первого вклада за несколько лет наращенная сумма будет равна
Для вклада, который был внесен в конце первого месяца, число периодов начисления процентов на один меньше, и формула будет выглядеть так
,
для третьего вклада — так
,
…
и для последнего вклада, то есть внесенного за месяц до окончания срока — так
,
Интересующий нас результат равен сумме всех этих выражений. И эти выражения кое-что роднит — все они члены геометрической прогрессии, в которой первый член равен , а знаменатель прогрессии равен .
Про геометрическую прогрессию смотри Геометрическая прогрессия
Таким образом, искомая сумма по формуле суммы геометрической прогрессии равна
Вот и все на сегодня.
Обновление
По просьбе пользователя добавлена возможность отдельного указания размера первого взноса.
planetcalc.ru
Чудо сложного процента
Один из Ротшильдов провозгласил сложный процент «восьмым чудом света». Глядя на то, как увеличиваются сегодня капиталы инвесторов, грамотно пользующихся его преимуществом, трудно с ним не согласиться.
Сложный процент – это начисление «процентов на проценты», когда доход, начисленный за один расчётный период, прибавляется к общей сумме вложенного капитала, и в следующий расчётный период процент начисляется уже на большую сумму. Процесс прибавления дохода к телу депозита называется капитализацией процентов.
Например, за год банк начисляет вам 10% от вклада в $1 000, и в конце года ваш вклад составляет $1 100. В течение следующего года, 10% будут начисляться уже на сумму $1 100, и под конец второго года ваш капитал составит уже не $1 200, а $1 210.
Конечно, это не самый впечатляющий пример – чтобы воспользоваться преимуществом сложного процента с банковской ставкой, придётся ждать десятилетия. Однако сегодня в распоряжении инвесторов есть еще одно чудо – международный валютный рынок Forex. Доход, полученный на этом рынке в результате даже одной сделки (которая может длиться от нескольких часов до нескольких дней), может поступить в работу в следующей сделке – сразу же!
Однако на форексе далеко не все (ха!) сделки являются прибыльными, поэтому расчёт сложного процента должен корректироваться математическим ожиданием, основанным на серии из многих предыдущих сделок. Поэтому наиболее разумной тактикой учёта для инвестора является использовать всё же ежемесячную (а не посделочную) капитализацию при прогнозировании прибыльности того или иного актива.
Сложный процент в истории

Один из отцов-основателей США Бенджамин Франклин (да, тот, который на стодолларовой купюре) после своей смерти в 1790 году оставил по 1 000 фунтов (или примерно $4 500) двум городам – Бостону (где он родился) и Филадельфии (где вырос), с условием, что они не будут трогать эти деньги в течение 200 лет. Правда, трасты, которым он оставил средства, не использовали фиксированную процентную ставку, а использовали эти средства под выдачу частных ссуд в разное время с разной процентной ставкой. Прошло 200 лет и наступило время снимать средства. К 1990 году трасты обоих городов добились разных результатов, но оба – впечатляющих, демонстрируя нам чудо сложного процента: Бостонский траст набрал около $5 000 000, а Филадельфия могла похвастать суммой в $2 000 000. Оба города решили использовать эти средства на основание различных учебных заведений и учреждения стипендий. (Я написал это, и вообразил, сколько бы эти деньги протянули в нашей стране и на что бы они в конце концов пошли. Стало смешно и грустно одновременно…)
Второй пример использования сложного процента также имеет отношение к финансовому гению американцев. В 1626 году голландские колонисты приобрели у индейцев Ленапе остров Манхэттен за тогдашний эквивалент $24 (в пересчёте на сегодняшние средства – около $1 000). Преподаватели экономики в американских университетах любят приводить в пример эту сделку, указывая на тот факт, что индейцы не распорядились деньгами должным образом. (Ну да, откуда им было про сложный процент знать-то. Теперь вот живут в резервациях и развлекают экскурсантов. Опять-таки, очень напоминает кого-то…). А суть в том, что вложи они средства хотя бы под 10% годовых (по тем временам уже вполне доступная процентная ставка), к сегодняшнему дню они могли бы выкупить обратно всю недвижимость Нью-Йорка, так как располагали бы суммой 100 триллионов долларов!
Ну, и немного абсурдный пример, показывающий, что – теоретически – могут сделать с мизерным капиталом тысячелетия. Известна евангельская притча о том, как одна бедная вдова во времена Иисуса Христа принесла в жертву в храм последнее, что у нее было – две самых мелких монеты, лепты. Отсюда, кстати, и пошло выражение «внести свою лепту». Если представить себе, что в то время существовали банки, и она внесла бы две монетки в банк, то какая сумма накопилась бы на банковском счете к сегодняшнему дню, учитывая, что банк обеспечивает капитализацию процентов в сумме, скажем, пять процентов годовых?
А расчёт показывает, что на сегодняшний день, наследники той вдовы (коих было бы, наверное, половина земного шара) имели бы в своём распоряжении капитал, равный 8.6 х 1031 лепт. Я, конечно, не знаю, сколько стоила тогда одна лепта, но если предположить её стоимость равной одному центу США, то этот капитал намного превысил бы все наличные и безналичные средства, находящиеся в обращении на нашей планете (примерно 10 квинтиллионов долларов).
Сложный процент в наши дни
Как я уже упомянул ранее, сегодня банковская процентная ставка является не самой привлекательной, хоть и считается эталоном надёжности. Сегодня частные лица имеют возможность вкладывать средства с разным балансом надёжности и доходности, но я в личных финансовых планах всегда ориентируюсь на процентную ставку 6% в месяц, с ежемесячной капитализацией. Примерно такую доходность пока что (уже на протяжении полугода) демонстрирует диверсифицированный памм-портфель, который я собрал. 6% в месяц, используя эффект сложного процента, обеспечивают ежегодное удвоение капитала.
Давайте посмотрим, за какой срок можно обеспечить себя пассивным доходом, равным вашей текущей зарплате (и таким образом, освободиться от необходимости работать, что и является моей целью), если иметь в распоряжении такой актив.
Предположим, наша зарплата составляет 100 единиц, т.е. процентов (для простоты расчёта). мы откладываем ежемесячно 1/10 часть зарплаты (10 единиц) и вкладываем эти деньги под 6% в месяц. Наша цель – собрать капитал размером 1 200 единиц. Этот капитал, удваиваясь за год, будет приносить нам 1 200 единиц дохода ежегодно, на которые мы сможем жить, получив те же 100 единиц в месяц, но уже не работая.
Итак:
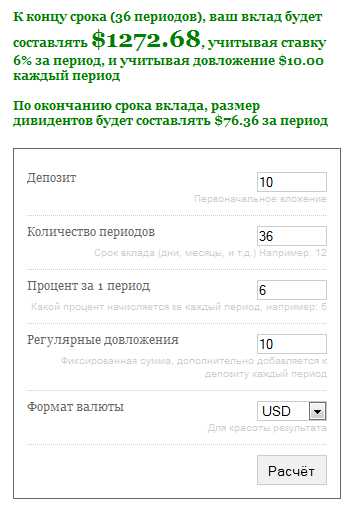
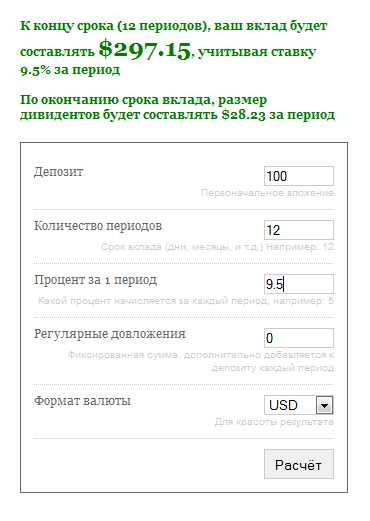
Обратите внимание на цифру в поле «количество периодов». Это количество месяцев: при первоначальном депозите в 10 единиц (поле «Депозит»), и последующем довложении в 10 единиц ежемесячно (поле «Регулярные довложения»), стабильной процентной ставке 6% в месяц, за 36 месяцев вы создадите капитал размером $1 200, а еще через год снимете свою годовую зарплату на следующие 12 месяцев, при этом ваш депозит останется $1 200, и отныне вы сможете поступать так ежегодно.
Вышеприведённый расчёт демонстрирует ещё одну особенность сложного процента, а именно – его способность многократно усиливать свой эффект при наличии регулярных довложений.
Конечно, вы можете возразить, что вкладывать средства под 6% в месяц довольно рискованно, и что активы, предлагающие подобную доходность, могут не протянуть такое время. Что ж, я придерживаюсь другой точки зрения, но не стану с вами спорить (оставлю силы для ответа на комментарии), а приведу вам примеры при более спокойных процентных ставках:
— Проинвестируйте всего $1 под 20% годовых и через 75 лет вы подарите наследникам… целый миллион долларов!
— Откладывайте всего по 1 доллару в день, инвестируйте полученные деньги под 20% годовых и через 35 лет вы порадуете своих детей все тем же миллионом долларов!
— Продолжайте инвестировать, и еще через 37 лет ваши внуки получат $1 000 000 000!
Правила и приёмы расчёта сложного процента
Прежде всего, следует понять, что правила арифметического расчёта (сложения) процентов тут не подойдут, так как мы имеем дело с умножением (геометрическим рядом). Следовательно, для расчёта суммы, получаемой при помощи сложного процента, следует возвести результат первого начисления процентов в степень, показателем которой будет число периодов.
Прямой расчет сложного процента
Упрощаем на примере:
— Было $5 000;
— Процентная ставка 10% за период (неважно какой период, например, год)
— Надо расчитать, какая сумма получится при вложении на 5 периодов (в нашем случае – лет).
Действия:
— прибавляем процентную ставку к единице: 1 + 0.1 = 1.1
— возводим в степень 5: (1.1)5 = 1.61
— множим наш депозит на это число: $5 000 * 1.61 = $8 052
Вот так-то вот.
Кстати возвести любое число в любую степень можно и без математического образования. Дядя Билл сделал всё за нас, открываем калькулятор Windows и переводим его в инженерный режим:
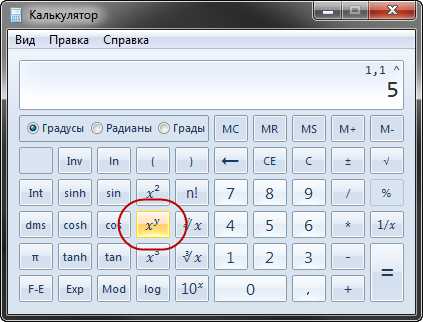
Набираем единицу с прибавленной процентной ставкой, потом вот ту хитрую кнопочку, потом степень (количество периодов), и жмём «равно».
Увы, калькулятор Windows не позволит расчитать сложный процент с учётом довложений, поэтому для таких расчётов оного я сделал специальный онлайн-калькулятор, которым вы можете пользоваться.
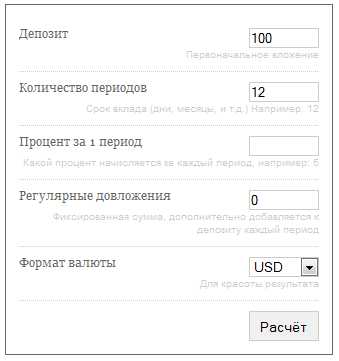
Несколько слов об его использовании:
— Калькулятор позволяет рассчитывать сложный процент для любого периода капитализации. Количество периодов вводится в поле «Количество периодов» (хе… спасибо, Кэп). Например, если проценты капитализируются ежедневно, то в это поле вводим срок инвестиции в днях. Например, 365 дней. А если проценты добавляются к депозиту ежемесячно, вводим срок в месяцах. И так далее.
— В поле «Процент» за период, соответственно, вводим процент, который добавляется к депозиту в конце каждого периода. Например, если у нас 6% в месяц, и мы прогнозируем годовой доход, то в поле «количество периодов» мы вводим 12 (месяцев), а в поле «процент», соответственно, 6 (процентов в один месяц).
— Поле «Депозит» обязательно должно быть отличным от нуля. Это надо помнить при расчётах типа «Сколько лет надо копить на «Запорожец», если откладывать каждый год по 10 баксов». В этом случае в депозит вы уже забиваете первые 10 баксов (вводите 10 в поле «Депозит»), это будет ваше вложение за первый год. В поле «количество периодов» начинаете методом перебора подбирать нужное число. Допустим, калькулятор говорит, что за 50 лет вы сможете собрать нужную сумму. Так вот, не забудьте прибавить первый год, когда вы вложили эти первые 10 баксов. Итого ваше искомое число – 51 год. (Ведь калькулятор начинает отсчитывать периоды с того момента, как ваш первоначальный депозит уже внесён).
— Поле «довложения» поможет вам, кроме добавления процентов к телу депозита в конце каждого периода, довносить какую-то фиксированную сумму, как в примере с зарплатой выше, и в примере с Запорожцем. Если вы не предполагаете так поступать, оставьте в этом поле ноль. Или же здесь может быть и отрицательное число (регулярное «снятие»).
Обратный расчёт сложного процента
Иногда требуется рассчитать, какую сумму надо вложить изначально, чтобы в результате за N периодов получить X. Для этого выполняем вот такую манипуляцию:
$10 000 / (1.1)5 = $6 209
Т.е. мы посчитали, что при ставке 10% (заложена в знаменателе в цифре 1.1) на 5 лет (знаменатель возводится в степень 5), чтобы получить $10 000 в конце (числитель), изначально нам следует вложить $6 209.
(Операция, обратная расчёту сложного процента, называется дисконтированием).
Расчёт средней доходности актива (процентной ставки)
Иногда требуется расcчитать, сколько в среднем приносит тот или иной актив, если мы знаем изначальное и конечное значение его стоимости. Особенно это полезно при расчёте средней ежемесячной доходности памм-счетов и других активов с непостоянной доходностью.
Допустим цена пая памм-счёта изначально составляла $100, а по окончании года она составляет $300. Требуется вычислить, сколько же в среднем в месяц приносит этот памм.
Конечно, вы уже поняли, что неверно взять всю прибыль ($200) и просто поделить на 12 (получится ставка где-то в районе 17%). Такой расчёт упускает из виду ежемесячную капитализацию процентов, особенно если памм использует прогрессирующий ММ (почти все паммы торгуют на определённый процент своего депозита, что и называется прогрессирующим мани-менеджментом, так как сумма, используемая в торговле, увеличивается с увеличением всего депозита в целом).
Вместо этого, нам необходимо извлечь корень 12-й степени из доходности счёта. Здесь нам на помощь приходит всё тот же инженерный калькулятор:
Доходность счёта = 300 / 100 = 3 (депозит увеличился втрое за 12 месяцев)
Корень 12-й степени из 3 = 1.095
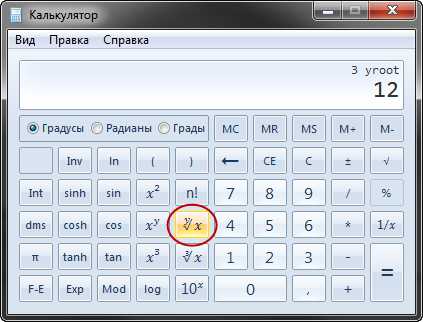
Отсюда вывод: средняя доходность данного памма = 9.5% в месяц. Проверяем на калькуляторе:
Примерно правильно!
Сколько ждать удвоения?
Можно использовать простое эмпирическое правило для определения того, как долго надо ждать удвоения суммы при данной процентной ставке. Оно называется «правилом 72». Просто поделите 72 на ставку процентов.
Пример: за сколько месяцев удвоится сумма, при процентной ставке 6% в месяц?
Ответ: 72 / 6 = 12 месяцев.
На этом заканчиваю свой краткий экскурс в увлекательный мир сложных процентов. Желаю всем удачных инвестиций и хороших профитов!
zenvestor.ru
Сложные проценты на примерах
Задачи на сложные проценты решаются в достаточно быстрый способ при знании нескольких простых формул. Часть из них касается начислений по вкладу или кредиту, когда те осуществляются через определенные промежутки времени . Также сложные проценты используют в задачах химии, медицины и ряде других сфер.
ФОРМУЛЫ СЛОЖНЫХ ПРОЦЕНТОВ
В случае размещения вкладов с капитализацией процентов на годы конечная сумма депозита определяется формулой
Здесь P – первоначальный взнос, r – процентная ставка, n – количество лет. По сложным процентам работают банки, инвестиционные фонды, страховые компании. Распространенные за рубежом, а теперь и в Украине — пенсионные фонды и фонды страхования жизни работают по схеме сложных процентов.
При размещении вкладов с капитализацией процентов ежеквартально формула сложных процентов будет выглядеть
где q – количество полных кварталов.
При капитализации процентов ежемесячно применяют следующую формулу для вычислений
где s – количество месяцев существования соглашения.
Последний случай, непрерывное начисление процентов, когда сложные проценты начисляются ежедневно, рассчитывают по формуле
где m – количество дней.
Страхование жизни и откладывания пенсий исчисляют сложными формулами, кроме начисления сложных процентов ежегодно осуществляются необходимые взносы.
Рассмотрим два случая накопления. Мужчина откладывает 5000 грн. в течение 20 лет. За это время он отложит
20*5000=100000 (грн).
При откладывании в накопительные фонды с годовой ставкой 13%, за первый год сумма возрастет до
5000*(1+13/100)=5650 (грн).
В следующем году человек в данной суммы добавляет еще 5000 грн. В результате, за второй год сумма увеличится
(5650+5000)*(1+0,13)=12034.50 (грн) .
Продолжая подобные вычисления, в конце срока получим сумму размером 457349,58 грн.
Поверьте — ошибок при исчислении форуме, большое значение набегает за счет сложных процентов. Сомнительным остается только история изменения платежеспособности гривны через 20 лет. Учитывая политику государства вкладывать деньги в такие фонды люди не спешат, однако за рубежом практика откладывания денег распространена, правда процентные ставки намного ниже.
Рассмотрим распространенные задачи на сложные проценты.
Пример 1. Вкладчик положил на депозит $ 3000 под 9% годовых на 10 лет. Какая сумма аккумулируется конце 10-го года при годовой капитализации? На сколько вырастет сумма по сравнению с первоначальным взносом?
Решение: Применяем формулу сложных процентов для нахождения суммы в конце срока
Чтобы ответить на второй вопрос, от значения 7102,09 вычитаем сумму вклада.
Разница составляет 4102 доллара.
Пример 2. Инвестор вложил 7000 грн под 10% годовых при условии начисления сложных процентов ежеквартально. Какую сумму он получит через 8 лет?
Решение: Применяем 2 формулу сложных процентов. Находим количество кварталов
8*4=32.
и подставляем в формулу
Школьные задачи на сложные проценты
Например, возьмем задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир «Аглгебра». (Номер в скобках)
Задача 1. (556) Костюм стоил 600 грн. После того как цена была снижена дважды, он стал стоить 432 грн., Причем процент снижения второй был в 2 раза больше, чем в первый раз. На сколько процентов каждый раз снижалась цена?
Решение: Для упрощения вычислений обозначим
X – первая скидка;
X/2 – вторая скидка.
Для вычисления неизвестной X составляем уравнение
Упрощаем, и сводим к квадратному уравнению
и решаем
Первый решение не имеет физического смысла, второй учитываем при вычислениях. Значение 0,2 соответствует снижению на 0,2*100%=20% после первой скидки, и X/2 =10% после второй скидки.
Задача 2. (557) Определенный товар стоил 200 грн. Сначала его цену повысили на несколько процентов, а затем снизили на столько же процентов, после чего стоимость его стала 192 грн. На сколько процентов каждый раз происходила смена цены товара?
Решение: Поскольку проценты одинаковы, то обозначаем изменении цены товара через X.
На основе условия задачи получим уравнение
Его упрощение приведет к решению уравнения
откуда корни приобретут значений
Первая значение отвергаем, оно меняет суть задачи (сначала имеем снижение, а затем рост процентов, противоречит условию). Второе при пересчете составит 0,2*100%=20% процентов.
Задача 3. (558) Вкладчик положил в банк 4000 грн. За первый год ему начислена определенный процент годовых, а второго года банковский процент увеличен на 4%. На конец второго года на счете стало 4664 грн. Сколько процентов составила банковская ставка в первый год?
Решение: Обозначим через X – увеличение вклада в первый год, тогда
X+4/100%=X+0,04
начисления во второй год.
По условию задачи составляем уравнение для определения неизвестной X
После упрощений получим квадратное уравнение вида
Вычисляем дискриминант
и корни уравнения
Первый корень отбрасываем, второй соответствует ставке в 6% годовых.
Задача 4. (564) В сосуде 12 кг кислоты. Часть кислоты отлили и долили до прежнего уровня водой. Затем снова отлили столько же, как и в первый раз, и долили водой до прежнего уровня. Сколько литров жидкости отливали каждый раз, если в результате получили 25-процентный раствор кислоты?
Решение: Обозначим через X – часть кислоты, которую отливали.
После первого раза ее осталось 12-X, а процентное содержание кислоты
После второй попытки содержание кислоты в сосуде составило
.
Разведя водой до 12 кг, процентное содержание составляло 25%. Составляем уравнение
Упрощаем проценты и избавляемся знаменателей
Решаем квадратное уравнение
Условии задачи удовлетворяет второе решение, а это значит, что каждый раз отливали 6 кг жидкости.
На этом знакомство со сложными процентами завершается. На практике Вам встретятся как простые так и сложные задачи. При проблемах с вычисления сложных процентов обращайтесь к нам, мы поможем Вам в решении задач.
yukhym.com
