Сколько будет 72 разделить на 6: сколько будет 72 разделить на 6

08.08.2019 alexxlab

Содержание

Сколько будет 72 разделить на 24. Как правильно объяснить ребёнку деление в столбик

Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.

Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям

Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.

Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».

Итак, как объяснить ребенку деление столбиком :

Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
Пусть ребенок сам разделит другое число, например, более сложное: 24:4
Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные

Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.

Начинайте с простого — деление на однозначное число:

Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.

Например, 256 разделить на 4:

Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
Спросите у малыша, сколько четверок помещается в двойке — нисколько
Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе

Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»

Письменное деление на двузначное число

Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.

Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.

Выполните вместе такое простое действие: 184:23 — как нужно объяснять:

Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8

Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.

Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:

Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно

Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.

Например:

Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864

Запишите 2864 под 2864, получается в разности 0. Ответ 204

Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.

Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.

Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.

Алгоритм деления чисел заключается в следующем:

Сделать прикидку числа, которое будет стоять в ответе
Найти первое неполное делимое
Определить число цифр в частном
Найти цифры в каждом разряде частного
Найти остаток (если он есть)

По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).

Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:

1428:42
2924:68
30296:56
136576:64
16514:718

Для закрепления результата можно использовать такие игры на деление:

«Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.

Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.

Видео: Игра арифметика для детей сложение вычитание деление умножение

Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2

Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .

В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.

Навигация по странице.

Правила записи при делении столбиком

Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.

Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105 , а делителем – 5 5, то их правильная запись при делении в столбик будет такой:

Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808 на 51 234 (614 808 – шестизначное число, 51 234 – пятизначное число, разница в количестве знаков в записях равна 6−5=1 ) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058 и 4 (здесь разница в количестве знаков равна 4−1=3 ).

Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:

Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.

Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком

Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.

Пример.

Пусть нам нужно разделить столбиком 8 на 2 .

Решение.

Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .

Но нас интересует, как выполнить деление этих чисел столбиком.

Сначала записываем делимое 8 и делитель 2 так, как того требует метод:

Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0 , 1 , 2 , 3 , … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.

Поехали: 2·0=0 ; 2·1=2 ; 2·2=4 ; 2·3=6 ; 2·4=8 . Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4 . При этом запись примет следующий вид:

Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.

В нашем примере получаем

Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).

Ответ:

8:2=4 .

Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.

Пример.

Разделим столбиком 7 на 3 .

Решение.

На начальном этапе запись выглядит так:

Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3 на 0 , 1 , 2 , 3 и т.д. до того момента, пока не получим число равное или большее, чем делимое 7 . Получаем 3·0=07 (при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6 (оно получено на предпоследнем шаге), а на место неполного частного записываем число 2 (на него проводилось умножение на предпоследнем шаге).

Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7 и 3 будет завершено.

Таким образом, неполное частное равно 2 , и остаток равен 1 .

Ответ:

7:3=2 (ост. 1) .

Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.

Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.

Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.

Первой слева цифрой в записи делимого 140 288 является цифра 1 . Число 1 меньше, чем делитель 4 , поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14 , с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.

Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.

Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x ). Для этого последовательно умножаем делитель на 0 , 1 , 2 , 3 , … до того момента, пока не получим число x или число больше, чем x . Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).

Умножаем делитель 4 на числа 0 , 1 , 2 , …, пока не получим число, которое равно 14 или больше 14 . Имеем 4·0=014 . Так как на последнем шаге мы получили число 16 , которое больше, чем 14 , то под выделенным числом записываем число 12 , которое получилось на предпоследнем шаге, а на место частного записываем число 3 , так как в предпоследнем пункте умножение проводилось именно на него.

На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.

Нам нужно вычесть столбиком из числа 14 число 12 (для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2 . Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2 меньше делителя 4 , то можно спокойно переходить к следующему пункту.

Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.

Под горизонтальной чертой справа от уже имеющейся там цифры 2 записываем цифру 0 , так как именно цифра 0 находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой образуется число 20 .

Это число 20 мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.

Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0

Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).

Под горизонтальной линией справа от запомненного места записываем цифру 2 , так как именно она находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2 .

Число 2 принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4 пунктов алгоритма.

Умножаем делитель на 0 , 1 , 2 и так далее, и сравниваем получающиеся числа с отмеченным числом 2 . Имеем 4·0=02 . Следовательно, под отмеченным числом записываем число 0 (оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0 (на 0 мы проводили умножение на предпоследнем шаге).

Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2

Под горизонтально чертой справа от числа 2 дописываем цифру 8 (так как она находится в этом столбце в записи делимого 140 288 ). Таким образом, под горизонтальной линией оказывается число 28 .

Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4 пунктов.

Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.

Осталось последний раз провести действия из пунктов 2 , 3 , 4 (предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288 и 4 в столбик:

Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.

Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).

Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.

Пример.

Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .

Решение.

На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида

После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид

Повторив цикл, будем иметь

Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136 и 9

Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .

Ответ:

7 136:9=792 (ост. 8) .

А этот пример демонстрирует, как должно выглядеть деление в столбик.

Пример.

Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .

Решение.

Удобнее всего выполнить деление столбиком.

Ответ:

7 042 035:7=1 006 005 .

Деление столбиком многозначных натуральных чисел

Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.

На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.

Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.

Пример.

Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .

Решение.

Так как в записи делителя 206 участвуют 3 знака, то смотрим на первые 3 цифры слева в записи делимого 5 562 . Эти цифры соответствуют числу 556 . Так как 556 больше, чем делитель 206 , то число 556 принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.

Теперь умножаем делитель 206 на числа 0 , 1 , 2 , 3 , … до того момента, пока не получим число, которое либо равно 556 , либо больше, чем 556 . Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556 . Так как мы получили число, которое больше числа 556 , то под выделенным числом записываем число 412 (оно было получено на предпоследнем шаге), а на место частного записываем число 2 (так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:

Выполняем вычитание столбиком. Получаем разность 144 , это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.

Под горизонтальной линией справа от имеющегося там числа записываем цифру 2 , так как она находится в записи делимого 5 562 в этом столбце:

Теперь мы работаем с числом 1 442 , выделяем его, и проходим пункты со второго по четвертый еще раз.

Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0

Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:

Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:

Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
Математика. Любые учебники для 5 классов общеобразовательных учреждений.

Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение.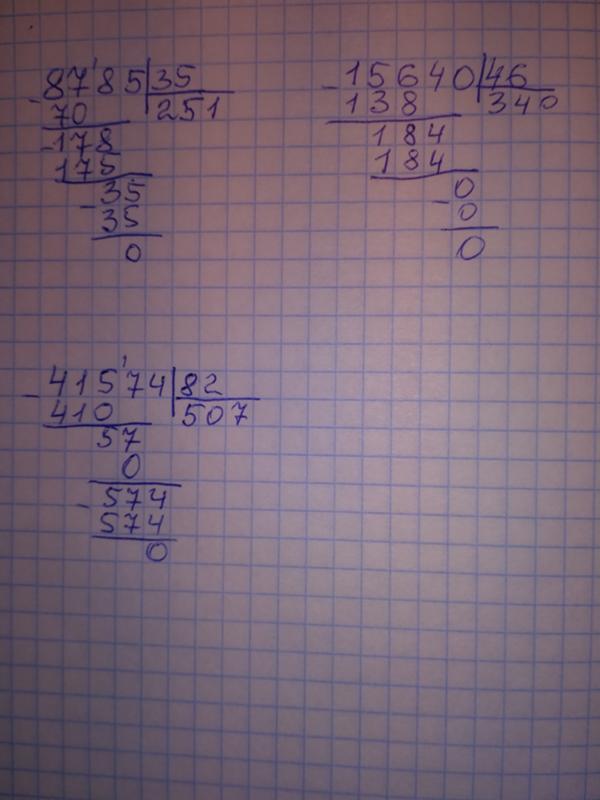 Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.

Особенности

Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .

Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:

Цифры.
Знаки арифметических действий.
Удаление раннее введенных символов.

Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.

Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:

умножение;
деление;
сложение;
вычитание.

Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.

Достоинства и недостатки

Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
Очень простой, интуитивно понятный интерфейс для каждого пользователя.
Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.

Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.

Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.

Как делить десятичные дроби на натуральные числа? Рассмотрим правило и его применение на примерах.

Чтобы разделить десятичную дробь на натуральное число, надо:

1) разделить десятичную дробь на число, не обращая внимания на запятую;

2) когда закончится деление целой части, в частном поставить запятую.

Примеры.

Разделить десятичные дроби:

Чтобы разделить десятичную дробь на натуральное число, делим, не обращая внимания на запятую. 5 на 6 не делится, поэтому в частном ставим нуль. Деление целой части окончено, в частном ставим запятую. Сносим нуль. 50 делим на 6. Берем по 8. 6∙8=48. От 50 вычитаем 48, в остатке получаем 2. Сносим 4. 24 делим на 6. Получаем 4. В остатке — нуль, значит, деление окончено: 5,04: 6 = 0,84.

2) 19,26: 18

Делим десятичную дробь на натуральное число, не обращая внимания на запятую. Делим 19 на 18. Берем по 1. Деление целой части окончено, в частном ставим запятую. Вычитаем от 19 18. В остатке — 1. Сносим 2. 12 на 18 не делится, в частном пишем нуль. Сносим 6. 126 делим на 18, получаем 7. Деление окончено: 19,26: 18 = 1,07.

Делим 86 на 25. Берем по 3. 25∙3=75. От 86 вычитаем 75. В остатке — 11. Деление целой части окончено, в частном ставим запятую. Сносим 5. Берем по 4. 25∙4=100. От 115 вычитаем 100. Остаток — 15. Сносим нуль. 150 делим на 25. Получаем 6. Деление окончено: 86,5: 25 = 3,46.

4) 0,1547: 17

Нуль на 17 не делится, в частном пишем нуль. Деление целой части окончено, в частном ставим запятую. Сносим 1. 1 на 17 не делится, в частном пишем нуль. Сносим 5. 15 на 17 не делится, в частном пишем нуль. Сносим 4. Делим 154 на 17. Берем по 9. 17∙9=153. От 154 вычитаем 153. В остатке — 1. Сносим 7. Делим 17 на 17. Получаем 1. Деление окончено: 0,1547: 17 = 0,0091.

5) Десятичная дробь может получиться и при делении двух натуральных чисел.

При делении 17 на 4 берем по 4. Деление целой части окончено, в частном ставим запятую. 4∙4=16. От 17 вычитаем 16. Остаток — 1. Сносим нуль. 10 делим на 4. Берем по 2. 4∙2=8. От 10 вычитаем 8. В остатке — 2. Сносим нуль. 20 делим на 4. Берем по 5. Деление окончено: 17: 4 = 4,25.

И еще пара примеров на деление десятичных дробей на натуральные числа:

Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.

Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).

Из этой статьи вы узнаете

Принцип деления для малышей

Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.

Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.

Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.

Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.

Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.

Как обучить малыша делению в столбик

Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.

Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.

Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.

При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.

Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.

Умножаем и делим с помощью таблицы

При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.

И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.

Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.

Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.

Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.

В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.

Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.

Делим с помощью столбика

Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.

Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.

В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.

Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.

Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.

Чтобы было проще обучить малыша процессу деления необходимо:

в 2-3 года понимание отношения целое-часть.
в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.

Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.

Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.

Деление столбиком. Онлайн калькулятор | Математика

Как записывать деление в столбик

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:

В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.

К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

780 : 12 = 65.

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

9027 : 9 = 1003.

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:

Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

3000 : 6 = 500.

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:

1340 : 23 = 58 (остаток 6).

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:

3 : 10 = 0 (остаток 3).

Калькулятор деления столбиком

Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.

Урок 42. деление числа на произведение. деление с остатком на 10, на 100, на 1 000 — Математика — 4 класс

Математика, 4 класс

Урок № 42. Деление числа на произведение. Деление с остатком на 10, на 100, на 1 000

Перечень вопросов, рассматриваемых в теме:

— как разделить число на произведение чисел?

— какие есть способы деления числа на произведение чисел?

Глоссарий по теме:

Деление – действие, обратное умножению. Деление заменяет неоднократное повторённое вычитание. Число, которое делят, называют делимым, число, на которое делят, называют делителем, результат деления называют частным.

Произведение – результат операции умножения.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2017. – с.25-26

2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.26

3. Волкова С. И. Математика. Проверочные работы.4 класс. М.: Просвещение, 2017. – с.60-61

Теоретический материал для самостоятельного изучения

Сегодня Миша отмечает свой день рождения. Он пригласил к себе 5 своих друзей. Перед приходом друзей они с мамой готовят угощения, пиццу и именинный пирог. Поскольку у мамы только одна форма для выпечки, пицца и пирог получились одинаковой прямоугольной формы. Всё уже на столе. Но вот проблема, как разделить пиццу и пирог на 6 равных частей, чтобы не обидеть никого из гостей?

Миша попросил маму помочь ему. Мама сказала, что разделить на 6 совсем не трудно, если вспомнить, что 6 – произведение чисел 2 и 3.

6 = 2 • 3

Разделим нашу пиццу на 2 половины. Затем каждую из полученных частей делим ещё на 3 равные части. Получилось 6 одинаковых по размеру кусков пиццы.

Тут к праздничному столу подошёл папа и предложил свой способ деления на 6. Он разделили пирог сначала на 3 части, а затем каждую из полученных частей ещё пополам, т.е. на 2. У папы тоже получилось 6 равных по размеру пирога. И Миша и его друзья были очень довольны. Итак, для деления на 6, мы использовали правило деления на произведение чисел.

Посмотри, как выглядит это правило в случае деления числа 12 на произведение чисел 2 и 3. Разделить число на произведение можно тремя способами:

— вычислить произведение и разделить на него число:

12 : (2 • 3) = 12 : 6 = 2

— разделить число на первый множитель и результат разделить на второй множитель:

12 : (2 • 3) = (12 : 2) : 3 = 6 : 3 = 2

— разделить число на второй множитель и результат разделить на первый множитель:

12 : (2 • 3) = (12 : 3) : 2 = 4 : 2 = 2

Ты можешь выполнять деление любым из этих способов. Но лучше выбирать тот, который будет наиболее удобным.

Посмотри, как правило деления числа на произведение упрощает нахождение частного чисел 560 и 14. Представим 14 в виде произведения чисел 7 и 2. Затем разделим число 560 на первый множитель 7, а полученный результат разделим на второй множитель 2. 560 разделить на 7 будет 80. 80 разделить на 2 получится 40.

560 : 14 = 560 : (7 • 2) = 560 : 7 : 2 = 80 : 2 = 40

А вот как выполняется деление на числа, оканчивающиеся нолями. Чтобы разделить 4800 на 800, представим 800 в виде произведения чисел 100 и 8. Разделим сначала 4800 на 100, получим 48. Теперь этот результат делим на 8, получаем 6. Обрати внимание, что деление числа 4800 на 800 можно заменить делением числа 48 на 8. Эти числа, полученные из делимого и делителя отбрасыванием двух нолей, находящихся справа в их записях.

4800 : 800 = 4800 : (100 • 8) = 4800 : 100 : 8 = 48 : 8 = 6

Задания тренировочного модуля:

1. К каждой записи первого столбца выбери соответствующую запись из второго столбца.

48 : (2 · 4)	96 : 4 : 8
63 : (3 · 7)	48 : 2 : 4
96 : (4 · 8)	63 : 3 : 7

Правильный ответ:

48 : (2 · 4)	48 : 2 : 4
63 : (3 · 7)	63 : 3 : 7
96 : (4 · 8)	96 : 4 : 8

2. Зачеркни неверные решения.

44 : (4 • 11) = 44 : 11 = 4

54 : (6 • 3) = 54 : 6 : 3 = 3

72 : (9 • 2) = 72 : 9 • 2 = 16

Правильный вариант:

Нужно зачеркнуть: 44 : (4 • 11) = 44 : 11 = 4 и 72 : (9 • 2) = 72 : 9 • 2 = 16.

3. Впиши пропущенные числа.

3600 : (4 • 100 ) =___

750 : (25 • 10) = ___

210 : (7 • 6) = ___

Правильный вариант: 9; 3; 5.

Деление в столбик ➗ примеры и правила, как научиться

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.

Рассмотрим пример деления трёхзначного числа на однозначное 322:7. Для начала определимся с терминами:

322 — делимое или то, что необходимо поделить;
7 — делитель или то, на что нужно поделить:
частное — результат действия.

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза. Проверяем 4*7=28, 28<32 все верно. Пишем 4 под чертой — это первая цифра частного. Между 32 и 28 ставим знак «минус», вычитаем по правилам и результат записываем под чертой.

Важно:

Результат вычитания должен быть меньше делителя.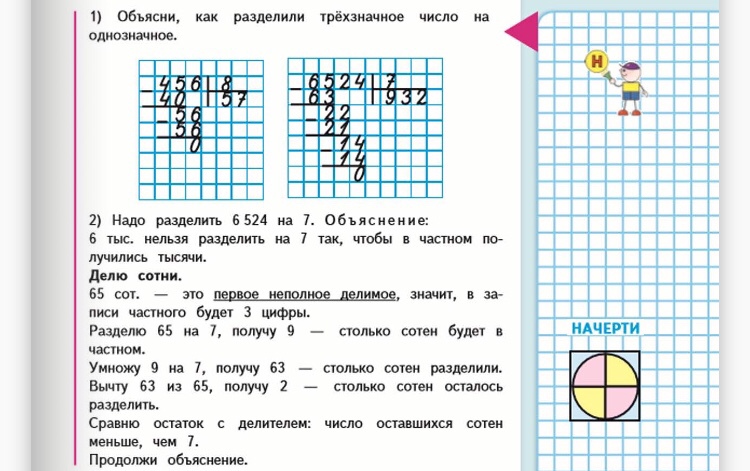 Если это не так, значит есть ошибка в расчете. Нужно увеличить выбранное число и выполнить действие еще раз.

Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся 2 и продолжаем размышлять.

Шаг 4. Сколько раз делитель 7 содержится в 42? Кажется, шесть раз. Проверяем 7*6=42, 42=42 все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Как выглядит деление в столбик с остатком

Это такое же деление, только в результате получается неровное число, как получилось в примере выше.

Например, делим 19 на 5. Наибольшее число, делящееся на 5 до 19 это 15. Проверяем 5*3=15, 19-15=4. Ответ: 3 и остаток 4. Записываем так: 19:5=3(4).
Еще пример: делим 29 на 6. Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).

Примеры на деление в столбик

Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!

Легкий уровень

Средний уровень

Сложный уровень

27:3=

48:4=

56:8=

72:9=

95:5=

270:15=

504:14=

315:5=

728:8=

855:9=

1749:11=

1080:45=

3888:72=

5248:64=

4818:66=

Ответы:

легкий уровень: 9; 12; 7; 8; 19;
средний уровень: 18; 36; 63; 91; 95;
сложный уровень: 159; 24; 54; 82; 73.

В детской школе Skysmart ученики решают примеры вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой. Запишите вашего ребенка на бесплатный вводный урок математики в Skysmart — мы покажем, что математика может быть увлекательным путешествием!

правила, примеры, решения, как целое число разделить на десятичную дробь

В этой статье мы разберем такое важное действие с десятичными дробями, как деление. Сначала сформулируем общие принципы, затем разберем, как правильно выполнять деление десятичных дробей столбиком как на другие дроби, так и на натуральные числа. Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на 0,1, 0,01, 100, 10 и др.

Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.

Основы деления десятичных дробей

Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.

Пример 1

Разделите 1,2 на 0,48.

Решение

Запишем десятичные дроби в виде обыкновенных. У нас получится:

1,2=1210=65

0,48=48100=1225.

Таким образом, нам надо разделить 65 на 1225. Считаем:

1,2:0,48=62:1225=65·2512=6·255·12=52

Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число 212, а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: 52=2,5.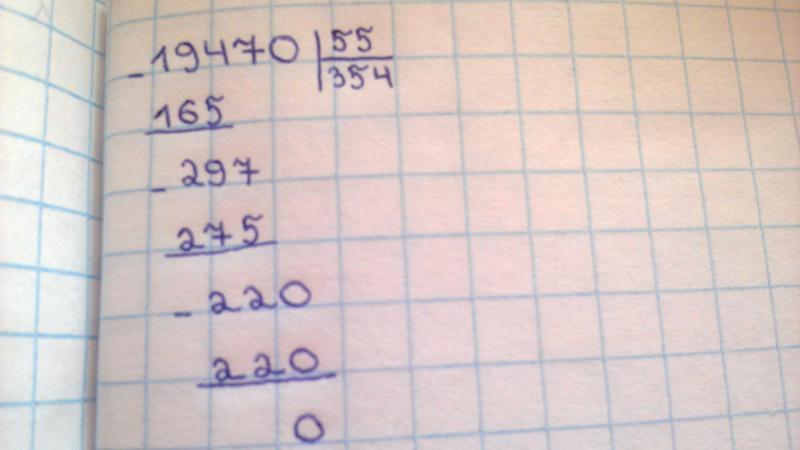 О том, как это сделать, мы уже писали ранее.

Ответ: 1,2:0,48=2,5.

Пример 2

Посчитайте, сколько будет 0,(504)0,56.

Решение

Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.

0,(504)=0,5041-0,001=0,5040,999=504999=56111

После этого конечную десятичную дробь также переведем в другой вид: 0,56=56100. Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:

0,(504):1,11=56111:56100=56111·10056=100111

У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:

Ответ: 0,(504):0,56=0,(900).

Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.

Пример 3

Найдите, сколько будет 0,779…/1,5602.

Решение

Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:

0,779…≈0,78

1,5602≈1,56

Можем продолжить подсчеты и получить примерный результат: 0,779…:1,5602≈0,78:1,56=78100:156100=78100·100156=78156=12=0,5.

Точность результата будет зависеть от степени округления.

Ответ: 0,779…:1,5602≈0,5.

Как разделить натуральное число на десятичную дробь и наоборот

Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.

Пример 4

Разделите 2,5 на 45.

Решение

Приведем 2,5 к виду обыкновенной дроби: 25510=512. Далее нам надо просто разделить ее на натуральное число. Делать это мы уже умеем:

25,5:45=512:45=512·145=1730

Если перевести результат в десятичную запись, то мы получим 0,5 (6).

Ответ: 25,5:45=0,5(6).

Как разделить десятичную дробь на натуральное число столбиком

Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.

Определение 1

Для деления столбиком десятичных дробей на натуральные числа необходимо:

1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).

2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.

Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.

Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.

Пример 5

Вычислите, сколько будет 65,144.

Решение

Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь 65,1400, которая будет равна исходной. Теперь пишем столбик для деления на 4:

Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:

Мы добрались до нулевого остатка, следовательно, процесс деления завершен.

Ответ: 65,14:4=16,285.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 6

Разделите 164,5 на 27.

Решение

Делим сначала дробную часть и получаем:

Отделяем полученную цифру запятой и продолжаем делить:

Мы видим, что остатки стали периодически повторяться, и в частном стали чередоваться цифры девять, два и пять. На этом мы остановимся и запишем ответ в виде периодической дроби 6,0(925).

Ответ: 164,5:27=6,0(925).

Как разделить столбиком одну десятичную дробь на другую

Такое деление можно свести к уже описанному выше процессу нахождения частного десятичной дроби и натурального числа. Для этого нам потребуется умножить делимое и делитель на 10, 100 и др. так, чтобы делитель превратился в натуральное число. Дальше выполняем описанную выше последовательность действий. Такой подход возможен благодаря свойствам деления и умножения. В буквенном виде мы записывали их так:

a:b=(a·10):(b·10), a:b=(a·100):(b·100) и так далее.

Сформулируем правило:

Определение 2

Для деления одной конечной десятичной дроби на другую необходимо:

1. Перенести запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, допишем в него нули с правой стороны.

2. После этого делим дробь столбиком на получившееся натуральное число.

Разберем конкретную задачу.

Пример 7

Разделите 7,287 на 2,1.

Решение: Чтобы делитель стал натуральным числом, нам надо перенести запятую на один знак вправо. Так мы перешли к делению десятичной дроби 72,87 на 21. Запишем полученные числа столбиком и вычислим

Ответ: 7,287:2,1=3,47

Пример 8

Вычислите 16,30,021.

Решение

Нам придется переносить запятую на три знака. В делителе для этого не хватит цифр, значит, нужно воспользоваться дополнительными нулями. Считаем, что получится в итоге:

Видим периодическое повторение остатков 4, 19, 1, 10, 16, 13. В частном повторяются 1, 9, 0, 4, 7 и 5. Тогда наш результат является периодической десятичной дробью 776,(190476).

Ответ: 16,3:0,021=776,(190476)

Описанный нами метод позволяет делать и наоборот, то есть делить натуральное число на конечную десятичную дробь. Посмотрим, как это делается.

Пример 9

Подсчитайте, сколько будет 3 5,4.

Решение

Очевидно, что нам придется перенести запятую вправо на один знак. После этого мы можем приступить к делению 30,0 на 54. Запишем данные столбиком и вычислим результат:

Повторение остатка дает нам в итоге число 0,(5), которое является периодической десятичной дробью.

Ответ: 3:5,4=0,(5).

Как разделить десятичные дроби на 1000, 100, 10 и др.

Согласно уже изученным правилам деления обыкновенных дробей, деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и др. Получается, чтобы выполнить деление, в данном случае достаточно просто перенести запятую на нужное количество цифр. Если значений в числе не хватит для переноса, нужно дописать нужное количество нулей.

Пример 10

Так, 56,21:10=5,621, а 0,32:100 000=0,0000032.

В случае с бесконечными десятичными дробями мы поступаем таким же образом.

Пример 11

Например, 3,(56):1 000=0,003(56) и 593,374…:100=5,93374….

Как разделить десятичные дроби на 0,001, 0,01, 0,1 и др.

Воспользовавшись тем же правилом, мы можем так же разделить дроби на указанные значения. Это действие будет аналогично умножению на 1000, 100, 10 соответственно. Для этого мы переносим запятую на одну, две или три цифры в зависимости от условий задачи и дописываем нули, если цифр в числе окажется недостаточно.

Пример 12

К примеру, 5,739:0,1=57,39 и 0,21:0,00001=21 000.

Это правило действует и в случае с бесконечными десятичными дробями. Советуем только быть внимательными с периодом дроби, которая получается в ответе.

Так, 7,5(716):0,01=757,(167), поскольку после того, как мы перенесли запятую в записи десятичной дроби 7,5716716716… на два знака вправо, у нас получилось 757,167167….

Если же у нас в примере непериодические дроби, то все обстоит проще: 394,38283…:0,001=394382,83….

Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот

Это действие мы также сводим к операциям с обыкновенными дробями. Для этого надо заменить десятичные числа соответствующими обыкновенными дробями, а смешанное число записать в виде неправильной дроби.

Если мы делим непериодическую дробь на обыкновенную либо на смешанное число, нужно поступить наоборот, заменив обыкновенную дробь или смешанное число соответствующей им десятичной дробью.

Страница 15 — ГДЗ Математика 3 класс. Моро, Бантова, Бельтюкова, Волкова, Степанова. Учебник часть 2

Вернуться к содержанию учебника

Деление суммы на число

Вопрос

Вспомни, как можно разделить сумму на число. Вычисли с устным объяснением:

(60 + 9) : 3

(30 + 12) : 3

(40 + 24) : 4

Закончи решение и объясни его:

36 : 2 = (20 + 16) : 2	78 : 2 = (60 + ) : 2 =
90 : 5 = (50 + ) : 5 =	96 : 4 = (80 + ) : 4 =

Подсказка

Чтобы разделить сумму на число, можно вычислить сумму и разделить её на число или разделить на число каждое слагаемое и полученные результаты сложить.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

1. Замени число 72 суммой таких двух слагаемых, чтобы его легко было разделить на 4, на 3, на 6.

Подсказка

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

84 : 6	3 • 18	86 : 2	68 ; 2
57 : 3	4 • 17	60 : 4	96 : 3
91 : 7	6 • 13	93 : 3	88 : 4

Подсказка

От перестановки множителей результат умножения не изменяется.

Чтобы умножить сумму на число, можно вычислить сумму и умножить её на число или умножить на число каждое слагаемое и полученные результаты сложить.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

3. В городе 3 театра, а библиотек я 6 раз больше. На сколько в городе больше библиотек, чем театров?

Подсказка

Чтобы узнать, на сколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее — вычитание.

Чтобы узнать, во сколько раз одно число больше или меньше другого, нужно узнать, сколько раз маленькое число содержится в большом — деление.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

4. Цена билета р. Пассажир отдал в кассу р. для покупки билетов. Сколько сдачи он должен получить?

Дополни условие и реши задачу.

Подсказка

Вариантов для решения этой задачи очень много. Мы предлагаем вставить числа 12, 100 и 3. Ты можешь вставить любые другие числа.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

39 : 3 • 4	100 — 3 • 4	84 — (48 + 26)
64 : 2 • 3	6 • 9 + 48 : 6	23 + (75 — 48)
48 : 4 • 8	66 : 3 • 2 — 5	53 — (53 — 40)

Подсказка

Повтори случаи табличного сложения и вычитания, умножения и деления, порядок действий при решении числовых выражений со скобками и без них.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

6. Найди и сравни длины ломаных.

Подсказка

Чтобы найти длину ломаной линии, нужно сложить длины всех её звеньев.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

7. Найди в многоугольниках прямые, острые и тупые углы. Выпиши их названия.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Вычисли. 64 : 4

7 • 12

50 : 2

39 : 3

Подсказка

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

Пользовательское соглашение

Деление на десятичную дробь | Математика

Деление на десятичную дробь сводится к делению на натуральное число.

Правило деления числа на десятичную дробь

Чтобы разделить число на десятичную дробь, надо и в делимом, и в делителе запятую перенести на столько цифр вправо, сколько их в делителе после запятой. После этого выполнить деление на натуральное число.

Примеры.

Выполнить деление на десятичную дробь:

1) 35,1 : 1,8

Чтобы разделить на десятичную дробь, нужно и в делимом, и в делителе перенести запятую на столько цифр вправо, сколько их после запятой в делителе, то есть, на один знак. Получаем: 35,1 : 1,8 =351 : 18. Теперь выполняем деление уголком. В итоге получаем: 35,1 : 1,8 = 19,5.

2) 14,76 : 3,6

Чтобы выполнить деление десятичных дробей, и в делимом, и в делителе переносим запятую вправо на один знак: 14,76 : 3,6 = 147,6 : 36. Теперь выполняем деление десятичной дроби на натуральное число. Результат: 14,76 : 3,6 = 4,1.

3) 70 : 1,75

Чтобы выполнить деление на десятичную дробь натурального числа, надо и в делимом, и в делителе перенести на столько знаков вправо, сколько их в делителе после запятой. Поскольку в делителе в этом случае запятая не пишется, недостающее количество знаков заполняем нулями: 70 : 1,75 = 7000 : 175. Делим уголком полученные натуральные числа: 70 : 1,75 = 7000 : 175 =40.

4) 0,1218 : 0,058

Чтобы разделить одну десятичную дробь на другую, переносим запятую вправо и в делимом, и в делителе на столько знаков, сколько их в делителе после запятой, то есть на три знака. Таким образом, 0,1218 : 0,058 = 121,8 : 58. Деление на десятичную дробь заменили делением на натуральное число. Делим уголком. Имеем: 0,1218 : 0,058 = 121,8 : 58 = 2,1.

5) 0,0456 : 3,8

И в делимом, и в делителе переносим запятую на один знак вправо. После этого делим десятичную дробь на натуральное число: 0,0456 : 3,8 = 0,456 : 38=0,012.

И еще пара примеров деления на десятичную дробь:

12,972 : 1,84 = 1297,2 : 184 = 7,05

268,8 : 0,56 = 26880 : 56 = 480

Что такое 72 делится на 6 с помощью длинного деления?

Смущает длинное деление? К концу этой статьи вы сможете разделить 72 на 6 с помощью деления в столбик и применить тот же метод к любой другой задаче деления в столбик! Давайте взглянем.

Хотите быстро выучить или показать учащимся, как решить 72, разделенное на 6, с помощью длинного деления? Воспроизведите это очень быстрое и веселое видео прямо сейчас!

Итак, первое, что нам нужно сделать, это уточнить термины, чтобы вы знали, что такое каждая часть деления:

Первое число 72 называется дивидендом.
Второе число 6 называется делителем.

Здесь мы разберем каждый шаг процесса деления в длину на 72, разделенные на 6, и объясним каждый из них, чтобы вы точно поняли, что происходит.

72 разделить на 6 пошаговое руководство

Шаг 1

Первым шагом является постановка нашей задачи деления с делителем слева и делимым справа, как показано ниже:

Шаг 2

Мы можем вычислить, что делитель (6) переходит в первую цифру делимого (7), 1 раз (а). Теперь, когда мы это знаем, можем поставить 1 вверху:

Шаг 3

Если мы умножим делитель на результат на предыдущем шаге (6 x 1 = 6), теперь мы можем добавить этот ответ под делимым:

Шаг 4

Затем мы вычтем результат предыдущего шага из второй цифры делимого (7-6 = 1) и запишем этот ответ ниже:

Шаг 5

Переместите вторую цифру делимого (2) вниз следующим образом:

Шаг 6

Делитель (6) переходит в нижнее число (12), 2 раза (а), поэтому мы можем поставить 2 сверху:

Шаг 7

Если мы умножим делитель на результат на предыдущем шаге (6 x 2 = 12), теперь мы можем добавить этот ответ под делимым:

Шаг 8

Затем мы вычтем результат предыдущего шага из третьей цифры делимого (12-12 = 0) и запишем этот ответ ниже:

Итак, каков ответ на 72 разделенное на 6?

Если вы дошли до этого урока, молодец! Больше нет цифр, которые можно было бы переместить из дивиденда, что означает, что мы выполнили задачу длинного деления.

Ваш ответ — это верхнее число, а любой остаток будет нижним числом. Итак, если 72 разделить на 6, окончательное решение будет:

Остаток 0

Цитируйте, ссылайтесь или ссылайтесь на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

Что 72 делится на 6 с помощью длинного деления?
«Сколько 72 будет разделено на 6 с использованием длинного деления?». VisualFractions.com . По состоянию на 9 мая 2021 г. https://visualfractions.com/calculator/long-division/what-is-72-divided-by-6-using-long-division/.
«Сколько 72 будет разделено на 6 с использованием длинного деления?». VisualFractions.com , https: // visualfractions.ru / калькулятор / long-div / what-is-72-div-by-6-using-long-div /. По состоянию на 9 мая 2021 г.
Что такое 72, разделенное на 6 с использованием длинного деления ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/long-division/what-is-72-divided-by-6-using-long-division/.

Дополнительные расчеты для вас

Теперь вы изучили метод деления числа 72 на 6 в столбик. Вот еще несколько способов вычисления:

Используя калькулятор, если вы наберете 72, разделив на 6, вы получите 12.
Вы также можете выразить 72/6 как смешанную дробь: 12 0/6
Если вы посмотрите на смешанную дробь 12 0/6, вы увидите, что числитель такой же, как остаток (0), знаменатель — это наш исходный делитель (6), а целое число — это наш окончательный ответ (12 ).

Калькулятор длинного деления

Введите другую задачу с длинным разделением для решения

Задача следующего длинного деления

Хотите более длинное деление, но не можете ввести два числа в калькулятор выше? Не волнуйтесь. Вот следующая проблема, которую вам необходимо решить:

Как 72 разделить на 7 с помощью длинного деления?

Задачи случайного длинного деления

Если вы дошли до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите задачи с длинным делением, да? Ниже приведены несколько случайно сгенерированных вычислений для вашего долгого удовольствия:

Деление десятичных знаков — Mental Math

Это полноценный урок для 5-6 классов с инструкциями и упражнениями, обучающими учащихся делить десятичные дроби с помощью математики в уме (на основе чувства чисел).Он начинается с некоторых разделов обмена, а затем объясняет их базовую стратегию. Студенты также делят десятичные дроби с помощью «деления измерения», например 0,45 ÷ 0,05, где мы думаем, сколько раз делитель входит в делимое. В уроке есть упражнения по шаблонам, задачи со словами, головоломка с числами и многое другое.

Здесь вы можете создавать рабочие листы для десятичного деления.

1. Сначала закрасьте детали. потом разделить и написать предложение о разделении.

а. Оттенок 0,3.
Разделить это на 3 части.

___ ÷ 3 = ___

б. Оттенок 0,64.
Разделить это на 2 части.

___ ÷ 2 = ___

г. Оттенок 1.8.
Разделить это на 3 части.

___ ÷ ___ = ___

г. Оттенок 1.6.
Разделить это на 4 части.

___ ÷ ___ = ___

e. Оттенок 0.30.
Разделить это на 10 частей.

___ ÷ ___ = ___

ф. Оттенок 0,1.
Разделить это на 10 частей.

___ ÷ ___ = ___

Десятичная дробь на целое число

Вы можете думать об умножении «Назад.”Чтобы решить 4,5 ÷ 5, подумайте: Какое число, умноженное на
на 5, даст дай мне 4.5? Или _____ × 5 = 4,5. Ответ — 0,9.
Или подумайте о « бананов, », разделенных среди группы людей. В единственное, на этот раз
«бананы» — это десятые, сотые или тысячные доли!
Например, 0,035 ÷ 5 равно « 35 тысячных разделить на 5 ”. Замените тысячные на бананы
на мгновение: « 35 бананов. делится на 5… равно 7 бананам. »Ответ на исходная задача
составляет 7 тысячных, или 0,007.
Другой пример: 0,12 ÷ 4 — это « 12 сотых разделить на 4 ». По сути, это задача деления
«12 разделить на 4», правда, в сотых долях. Ответ — 3 сотых или 0,03.

2. Напишите задачи деления с числами и решите.

а. 9 десятые разделить на 3 равно…	_______ ÷ ____ = _______
г. 72 тысячные, разделенные на 9, равняются …	_______ ÷ ____ = _______
г. 54 деление сотых на 6 дает …	_______ ÷ ____ = _______
г. 240 тысячных разделить на 60 равно …	_______ ÷ ____ = _______
e. 122 сотые разделить на 2 равно…	_______ ÷ ____ = _______

3. Разделить. Подумайте о делении «бананов»: как вы делите много десятых, сотых или тысячных долей.
Или подумайте об умножении в обратном направлении.

а. 0,024 ÷ 6 = ______

г. 0,24 ÷ 6 = _______

с. 2,4 ÷ 6 = ________

г. 0,49 ÷ 7 = _______

e. 1.2 ÷ 3 = ________

ф. 0,056 ÷ 7 = _______

г. 5,40 ÷ 9 = _______

ч. 0,20 ÷ 4 = ________

i. 0,050 ÷ 10 = _______

Обманывать! Помните, как 0,40 = 0,4? Мы можем опустить десятичный ноль, но мы также можем Напиши это. Когда деление десятичной дроби на целое число часто помогает «пометить» а нуль от числа до деления.

0,8 ÷ 100 (отметьте два нуля)

→ 0,800 ÷ 100 = 0,008

(800 тысячных разделенных на 100
равно 8 тысячных)

0,7 ÷ 10 (отметьте один ноль)

→ 0,70 ÷ 10 = 0,07

(70 сотых разделить на 10
равно 7 сотым.)

4 ÷ 8 (отметьте один ноль)

→ 4,0 ÷ 8 = 0,5

(40 десятых разделить на 8
равняется 5 десятым.)

4. Разделить. Отметьте дивиденд нулем или нулями.

а. 0,3 ÷ 5 = ________

г. 0,3 ÷ 10 = ________

c. 3 ÷ 5 = ________

г. 0,06 ÷ 12 = _______

e. 0,2 ÷ 40 = _______

ф. 2 ÷ 5 = _______

г. 0,3 ÷ 50 = ________

ч. 0,7 ÷ 100 = ________

i. 0,02 ÷ 10 = ________

5. Джейн разделила 2 доллара поровну среди пяти друзей.
Сколько получил каждый?

6. Если каждое сердцебиение длится 0,8 секунды, сколько времени длится пять ударов сердца?

Десять ударов сердца?

7. Напишите две задачи деления. и две задачи умножения с одинаковыми числами — семейство фактов!

а. 8 × 0,04 = 0,32

_____ × _____ = ______

_____ ÷ _____ = ______

б. ____ × ____ = _____

____ × ____ = _____

2 ÷ 0,4 = 5

____ ÷ ____ = _____

г. ______ × ______ = _______

______ × ______ = _______

______ ÷ ______ = _______

0,025 ÷ 5 = 0,005

Иногда помогает подумать , сколько раз делитель « идет на » или «Вписывается» в дивиденды .

Пример 1. 0,24 ÷ 0,03 =? Подумайте: « Как много раз будет 3 сотые переходят в 24 сотые? ”
Точно так же, как 3 превращается в 24 восемь раз, 3 сотые входят в 24 сотых 8 раз .

Пример 2. Мама отрезала кусочки длиной 0,4 метра из кусок материала длиной 1,2 метра.
Сколько штук она получила?

Подумайте: «Сколько раз 0,4 превратится в 1,2?» В ответ конечно простой: 3 раза.
Мы также можем написать деление из этой ситуации: 1,2 ÷ 0,4 = 3.

8. Разделить. Подумайте: сколько раз идет ли делитель на дивиденд?

а. 4,5 ÷ 0,5 = _______

г. 0,45 ÷ 0,05 = _______

г. 0,450 ÷ 0,005 = _______

г. 0,12 ÷ 0,06 = _______

e. 0,006 ÷ 0,002 = ______

ф. 0,63 ÷ 0,07 = ________

г. 2,1 ÷ 0,7 = ________

ч. 1,5 ÷ 0,3 = ________

i. 0,09 ÷ 0,01 = _______

9. Напишите деление предложение для каждой проблемы и решить.

а. Сколько кусков 0,3 м вы получите из 1,8 м ткани? _______ ÷ _____ = ________

г. Сколько штук 0,7 м получится из 4.2 м дерева? _______ ÷ _____ = ________

г. Сколько 0,05 м штук ты получить из 0,25 м веревки? _______ ÷ _____ = ________

Пример 3. 0,72 ÷ 0,008 = ?

Во-первых, тега ноль на 0,72, так что также имеет три десятичных знака, просто например, 0,008 имеет три десятичных знака.
Теперь получаем: 0,720 ÷ 0,008 = ?

Теперь подумайте: «Как много раз 8 тысячных умещается в 720 тысячных? »
Это то же самое, что спросить: «Сколько раз 8 умещается в 720?»

Ответ: 90 раз. Итак, 0,720 ÷ 0,008 = 90 ( не 0,90 или 0,090; просто равнина 90).

10. Разделить. Возможно, вам потребуется пометить ноль или нули в делимом так, чтобы оба числа имели одинаковое количество десятичных цифр
. Затем подумайте: сколько раз делитель входит в дивиденд?

а. 0,20 ÷ 0,05 = _______

г. 0,3 ÷ 0,05 = _______

г. 1 ÷ 0.2 = _______

e. 5 ÷ 0,2 = _______

г. 0,4 ÷ 0,02 = _______

ф. 0,05 ÷ 0,001 = _______

г. 0,6 ÷ 0,05 = _______

Дж. 1 ÷ 0,02 = _______

ч. 0,9 ÷ 0,01 = _______

к. 1 ÷ 0,01 = _______

и. 0,1 ÷ 0,01 = _______

л. 0,03 ÷ 0,002 = _______

11. The асфальтовая бригада каждый день проезжает 1,2 мили по дороге.

а. Сколько дней им нужно, чтобы преодолеть расстояние в 6 миль?

б. Сколько дней им нужно, чтобы преодолеть расстояние в 60 миль?

12. У Джека в кармане 1,45 доллара.

а. Сколько пятаков у Джека?

г. Введите десятичную дробь, если вы еще этого не сделали. деление, чтобы соответствовать проблеме.

13. Сколько 0,04-метровых палочек можно вырезать из 0,20-метровой доски?
Введите десятичное деление, соответствующее задаче.

14. Какие выражения соответствуют проблема?
Есть два. (Ты не должен что угодно посчитать.)

Одна книга толщиной 3 см лежит в ящике высотой
см.Сколько книг
толщиной 1,5 см можно сложить в эту коробку?

8 × 1,5 см + 3 см = 15 см

15 × 3 см + 1,5 см = 46,5 см

(15 см — 3 см) ÷ 1,5 см = 8

(15 см — 1,5 см) ÷ 3 см = 4,5

15 см + 3 см + 1,5 см = 19,5 см

(15 см ÷ 3 см) + 1,5 см = 6,5

(15 см ÷ 1,5) + 3 см = 13

15. Напишите сингл выражение (числовое предложение с несколькими операциями), чтобы решить эту проблему.Решать.

Сколько осталось от 5 метров материала
после того, как вы отрежете четыре куска по 0,6 метра?

16. У Джо 0,85 кг мяса. Сколько порций по 0,3 кг он может получить от этого?

Кроме того, «конвертируйте» эту задачу в граммы, помня, что в 1 кг 1000 грамм.

17. Разделите и разместите ответы. в головоломке с крестиком.

Поперечный:

а. 1 ÷ 0,04

г. 0,018 ÷ 9

с. 0,044 ÷ 0,004

г. 5 ÷ 10

e. 0,9 ÷ 0,09

Вниз:

а. 0,9 ÷ 0,06

б. 0,09 ÷ 3

с. 8,4 ÷ 0,7

д. 1 ÷ 100

e. 0,32 ÷ 8

18.Выясните шаблон и продолжайте как минимум еще две задачи.

а. 0,025 ÷ 0,005 =

0,25 ÷ 0,05 =

2,5 ÷ 0,5 =

б. 1000 ÷ 20 =

100 ÷ 2 =

10 ÷ 0,2 =

c. 4200 ÷ 40 =

420 ÷ 4 =

42 ÷ 0.4 =

Основываясь на том, что вы наблюдали в предыдущий упражнение, изменение
десятичное деление 0,987 ÷ 0,021 в ЦЕЛОЕ ЧИСЛО
проблема разделения с тем же ответом, и решить.

Этот урок взят из книги Марии Миллер Math Mammoth Decimals 2, размещенной на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер. Он соответствует Общему базовому стандарту для 5-го класса 5.NBT.7.

Математика Мамонт Десятичные 2

Самообучающийся рабочий текст для 5-6 классов, охватывающий четыре операции с десятичными знаками до трех десятичных знаков, с упором на десятичное умножение и деление. В книге также рассматриваются разряды, сравнение, округление, сложение и вычитание десятичных знаков. Есть много проблем с умственной математикой.

Скачать (6,25 $) . Также имеется в виде печатной копии.

=> Узнайте больше и посмотрите бесплатные образцы!

72 разделить на 12 | 72 разделить на 12 с остатком

Ответ на математические задачи Этапы решения

Математические ответы на деление дроби 72/12

7212 = 6

6 = 60 с точностью до десятых

6 = 6 с точностью до сотых

6 = 6 с точностью до тысячных

= 0 с точностью до десятых

= 0 с точностью до сотых

= 0 с точностью до тысячных

Другие разделы Домашнее задание по математике —

72 разделить пополам плюс 20

Домашнее задание ответов: (72/2) + 20 = 56

72 разделить пополам плюс 40

Домашнее задание ответов: (72/2) + 40 = 76

72/12 разделить на 2

Ответ: (72/12) ÷ 2 = 3

С помощью этого бесплатного инструмента можно легко решить домашнее задание по математике

Division.Чтобы решить домашнее задание или задание, все, что вам нужно сделать, это ввести значение в соответствующее поле и нажать «вычислить», чтобы получить математические ответы.

Что такое числитель / знаменатель

Числитель: мы называем верхнее число числителем, это число в верхней части имеющейся у вас дроби.

Знаменатель: мы называем нижнее число знаменателем, это целое число внизу, это число, на которое делится.

Шаги преобразования дробной части в десятичную

Шаг 1: Найдите число, которое можно умножить на нижнюю часть дроби, чтобы получилось 10, 100, 1000 или любая единица с последующими нулями.

Шаг 2: Умножьте верхнюю и нижнюю часть на выбранное вами число.

Шаг 3. Затем запишите только верхнее число, поместив десятичную запятую в правильное место, то есть на один пробел с правой стороны для каждого нуля в нижнем числе.

a / b = c В приведенных выше выражениях a называется делимым, b называется делителем, а c называется частным; в выражении a / b, a также называется числителем, а b также называется знаменателем.

Этот калькулятор дробей также можно использовать для вычисления доли в процентах, скидок на покупки, купонов, жировых отложений, валовой прибыли, потери веса, любви, налогов, увеличения и уменьшения населения, прибыли от продаж.Как только вы знаете значения, определить% легко.

Если вы обнаружите ошибку на этом сайте, мы будем благодарны, если вы сообщите нам об этом, используя предоставленный контактный адрес электронной почты. отправьте электронное письмо контакту на нашем сайте.

Далее Назад

Десятичные дроби

Делить на десятичные дроби немного сложно. В наши дни большинство учителей не возражают, если вы воспользуетесь калькулятором. Но хорошо знать, как сделать это самому, и вам всегда нужно уметь оценивать ответ, чтобы вы могли убедиться, что ответ калькулятора разумный.

Напомним, что в задаче Икс ÷ y знак равно z , также написано

y z Икс

Икс называется дивиденд , y это делитель , а также z это частное .

Шаг 1: Оцените ответ округление . Вы будете использовать эту оценку, чтобы проверить свой ответ позже.

Шаг 2: Если делитель не целое число, переместите десятичный разряд п места справа, чтобы превратить его в целое число. Затем переместите десятичный знак в делимом на такое же количество разрядов вправо (при необходимости добавив несколько дополнительных нулей).

Шаг 3: Делить как обычно. Если делитель не входит равномерно, добавьте нули справа от дивиденда и продолжайте делить, пока не получите 0 остаток или пока не появится повторяющийся узор.

Шаг 4: Поместите десятичную запятую в частное прямо над тем местом, где теперь десятичная запятая в делимом.

Шаг 5: Сравните свой ответ со своей оценкой, чтобы увидеть, разумен ли он.

Пример:

Делить.

0,45 ÷ 3,6

Шаг 1: Поскольку делитель больше делимого, мы получим ответ меньше, чем 1 .С 0,45 примерно в десять раз меньше 3,6 , мы ожидаем ответа, близкого к 0,1 .

Шаг 2: Делитель не является целым числом, поэтому переместите десятичную запятую на одну позицию вправо, чтобы сделать ее целым числом. Также переместите десятичную запятую в делимом на одну позицию вправо.

36 4.5

Шаг 3: Делите нормально, добавляя дополнительные нули справа от 4.5 когда вы закончите.

36 125 4.500 3 6 _ 90 72 _ 180 180 _ 0

Шаг 4: Поместите десятичную точку в частном непосредственно над десятичной точкой в делимом.

36 0,125 4.500 3 6 _ 90 72 _ 180 180 _ 0

Мы получили 0.125 .

Шаг 5: Сравните с вашей первоначальной оценкой. 0,125 близко к 0,1 , так что у нас все хорошо!

Иногда проще решить задачу десятичного деления с помощью мысленной математики. Это хорошая стратегия, когда вы видите, что, перемещая десятичные точки, вы можете превратить проблему в ту, на которую вы запомнили ответ.

Пример:

Делить.

0,42 ÷ 70

Мы знаем это 42 ÷ 7 знак равно 6 .

Если дивиденд является уменьшился с коэффициентом 10 , то коэффициент также уменьшится в 10 .

42 ÷ 7 знак равно 6 4.2 ÷ 7 знак равно 0.6 0,42 ÷ 7 знак равно 0,06

И если делитель является выросла с коэффициентом 10 , то коэффициент уменьшится в 10 .

0,42 ÷ 70 знак равно 0,006

Итак, ответ 0,006 .

Дивизион ÷ | Основы арифметики

На этой странице представлены основные сведения о Дивизионе (÷) .

См. Другие наши арифметические страницы для обсуждения и примеров: Сложение ( + ), Вычитание (-) и Умножение ( × ).

Дивизион

Обычный письменный символ деления — (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).

Деление — это противоположность умножения в математике.

Деление часто считается самой сложной из четырех основных арифметических функций.На этой странице объясняется, как выполнять расчеты деления. Когда мы хорошо разбираемся в методе и правилах, мы можем без ошибок использовать калькулятор для более сложных вычислений.

Дивизион позволяет нам разделить или «поделиться» числами, чтобы найти ответ. Например, давайте посмотрим, как мы можем найти ответ на 10 ÷ 2 (десять, разделенные на два). Это то же самое, что «разделить» 10 сладостей между 2 детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ — 5.

Некоторые быстрые правила о делении:

Если вы разделите 0 на другое число, ответ всегда будет 0. Например: 0 ÷ 2 = 0. То есть 0 сладостей, поровну разделенных между 2 детьми — каждый ребенок получает 0 сладостей.
Когда вы делите число на 0, вы вообще не делите (это большая проблема в математике). 2 ÷ 0 невозможно. У вас есть 2 сладости, но нет детей, чтобы разделить их между собой. Нельзя делить на 0.
Когда вы делите на 1, ответ будет таким же, как и число, которое вы делили.2 ÷ 1 = 2. Две сладости, разделенные на одного ребенка.
Когда вы делите на 2, вы уменьшаете число вдвое. 2 ÷ 2 = 1.
Любое число, разделенное на такое же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет, разделенных на двадцать детей — каждый ребенок получает по одной конфете.
Номера должны быть разделены в правильном порядке. 10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять сладостей, разделенных на двоих детей, очень отличаются от двух сладостей, разделенных на 10 детей.
Все дроби, такие как ½, ¼ и ¾, являются суммами деления.½ — это 1 ÷ 2. Одна конфета, разделенная на двоих детей. Смотрите нашу страницу Дроби для получения дополнительной информации.

Множественное вычитание

Так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.

Например:

Если у Джона есть 10 галлонов топлива в машине и он использует 2 галлона в день, сколько дней до того, как он закончится?

Мы можем решить эту проблему, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.

В день 1 Джон начинает с 10 галлона и заканчивается 8 галлонами. 10-2 = 8
В день 2 Джон начинает с 8 галлона и заканчивается 6 галлона. 8 — 2 = 6
В день 3 Джон начинает с 6 галлона и заканчивается с 4 галлона. 6 — 2 = 4
В день 4 Джон начинает с 4 галлона и заканчивается с 2 галлона. 4–2 = 2
В день 5 Джон начинает с 2 галлона и заканчивается 0 галлонами. 2–2 = 0

У Джона заканчивается топливо на пятый день.

Более быстрый способ выполнить этот расчет — разделить 10 на 2. То есть сколько раз 2 уходит в 10 или сколько партий по два галлона в десяти галлонах? 10 ÷ 2 = 5.

Таблица умножения (см. Умножение) может помочь нам найти ответ на простые вычисления деления.

В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (заштрихованный красным заголовок). Двигайтесь вниз по столбцу, пока не найдете искомый номер: 10 . Перемещайтесь по строке влево, чтобы увидеть ответ (заштрихованный красным заголовок) 5 .

Таблица умножения

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Мы можем выполнить другие простые вычисления деления, используя тот же метод.Например, 56 ÷ 8 = 7 . Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки, 8 .

Если возможно, вам следует попытаться запомнить приведенную выше таблицу умножения, потому что она значительно ускоряет решение простых вычислений умножения и деления.

Деление больших чисел

Вы можете использовать калькулятор для вычисления деления, особенно когда вы делите большие числа, которые труднее вычислить в уме.Однако важно понимать, как выполнять расчеты деления вручную. Это полезно, когда у вас нет под рукой калькулятора, но также необходимо для того, чтобы убедиться, что вы правильно используете калькулятор и не делаете ошибок. Деление может показаться устрашающим, но на самом деле, как и в большинстве арифметических операций, оно логично.

Как и всю математику, проще всего понять, если мы рассмотрим пример:

Машине Дэйва нужны новые шины. Ему нужно заменить все четыре шины на машине, а также запасную.

Дэйв получил предложение от местного гаража на сумму 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?

Задача, которую нам нужно вычислить, — это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 перейдет в 480?

Условно мы пишем это как:

Мы работаем слева направо в логической системе.

Мы начинаем с деления 4 на 5 и сразу же решаем задачу. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.

Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «Сколько раз 5 переходит в 4?».

Мы знаем, что 2 дважды переходит в 4 (4 ÷ 2 = 2), и мы знаем, что 1 переходит в 4 четыре раза (4 ÷ 1 = 4), но 5 не переходит в 4, потому что 5 больше 4.

Число, на которое мы делим (в данном случае 5), должно войти в число, на которое мы делим (в данном случае 4) целое количество раз. Как вы увидите, это необязательно должно быть точное целое число.

Поскольку 5 не переходит в 4, мы помещаем 0 в первый столбец (сотни). Для получения помощи с столбцами сотен, десятков и единиц см. Нашу страницу , числа .

	Сот	Десятки	шт.
	0
5	4	8	0

Затем мы переместимся вправо, чтобы включить столбец десятков.Теперь мы можем увидеть, сколько раз 5 переходит в 48.

5 действительно переходит в 48, поскольку 48 больше 5. Однако нам нужно выяснить, сколько раз оно идет.

Если мы обратимся к нашей таблице умножения, то увидим, что 9 × 5 = 45 и 10 × 5 = 50 .

48 , число, которое мы ищем, находится между этими двумя значениями. Помните, что нас интересует целое число раз , что 5 переходит в 48. Десять раз — это слишком много.

Мы можем видеть, что 5 переходит в 48 целое число (9) раз, но не точно, с оставшимися 3.

9 × 5 = 45
48-45 = 3

Теперь мы можем сказать, что 5 делится на 48 девять раз, но с остатком 3. Остаток — это то, что остается, когда мы вычитаем найденное число из числа, на которое делим: 48-45 = 3 .

Итак, 5 × 9 = 45, + 3, чтобы получить 48.

Мы можем ввести 9 в столбец десятков в качестве ответа для второй части расчета и поставить остаток перед нашим последним числом в столбце единиц.Наше последнее число становится 30.

	Сот	Десятки	шт.
	0	9
5	4	8	30

Теперь разделим 30 на 5 (или узнаем, сколько раз 5 делится на 30). Используя нашу таблицу умножения, мы можем увидеть, что ответ — ровно 6 без остатка. 5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.

	Сот	Десятки	шт.
	0	9	6
5	4	8	30

Поскольку остатков нет, мы закончили расчет и получили ответ 96 .

Новые шины Дэйва будут стоить £ 96 каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .

Отдел рецептов

Наш последний пример деления основан на рецепте. Часто при приготовлении рецепты сообщают вам, сколько еды они собираются приготовить, например, чтобы накормить 6 человек.

Ингредиенты, указанные ниже, необходимы для изготовления 24 сказочных лепешек, однако мы хотим приготовить только 8 сказочных лепешек. Мы немного изменили ингредиенты для удобства этого примера (оригинальный рецепт на сайте BBC Food).

Первое, что нам нужно установить, это сколько восьмерок в 24 — используйте приведенную выше таблицу умножения или свою память.3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Следовательно, нам нужно разделить каждый ингредиент, указанный ниже, на 3, чтобы получить необходимое количество смеси для изготовления 8 сказочных лепешек.

Состав

120 г сливочного масла, размягченного при комнатной температуре
120 г сахарной пудры
3 яйца от кур на свободном выгуле, слегка взбитые
1 чайная ложка ванильного экстракта
120 г муки самоподъемной
1-2 столовые ложки молока

Количество масла, сахара и муки все одинаково, 120гр.Следовательно, необходимо всего один раз проработать 120 ÷ 3, поскольку для этих трех ингредиентов ответ будет одинаковым.

Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3. Однако 3 ÷ 1 не идет, поскольку 3 больше 1. Затем мы смотрим, сколько умножений 3 получается в 12. Используя таблицу умножения если необходимо, мы можем увидеть, что 3 переходит в 12 ровно 4 умноженных на без остатка.

120 г ÷ 3, следовательно, 40 г. Теперь мы знаем, что нам понадобится 40 г масла, сахара и муки.

Исходный рецепт требует 3 яйца, и мы снова делим на 3. Итак, 3 ÷ 3 = 1, поэтому необходимо одно яйцо.

Далее рецепт требует 1 чайную ложку ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 то же самое, что third (одна треть). Вам понадобится чайной ложки ванильного экстракта, хотя на самом деле сложно точно отмерить чайной ложки!

Оценка может быть полезной, а единицы измерения можно менять!

Мы можем взглянуть на это с другой стороны, если знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам.(Если вам нужна помощь с единицами измерения, см. Нашу страницу Системы измерения .) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 делится на 5 один раз (3) с оставшимися 2. 2 ÷ 3 — это то же самое, что и so, поэтому 5 мл, разделенное на 3, дает 1 ⅔ мл, что в десятичных дробях составляет 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, немного больше полутора миллилитров. Если у вас на кухне есть крошечные мерные ложки, вы можете быть очень точными!

Мы можем оценить ответ, чтобы убедиться, что мы правы.Три партии по 1,5 мл дают нам 4,5 мл. Итак, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшие оценки могут быть забавой и хорошей практикой для нашей ментальной арифметики.

Следующий рецепт требует 1-2 ст. Л. Молока. Это от 1 до 2 столовых ложек молока. У нас нет точного количества, и то, сколько молока вы добавите, будет зависеть от консистенции вашей смеси.

Мы уже знаем, что 1 ÷ 3 — это ⅓, а 2 ÷ 3 -.Поэтому нам понадобится – столовой ложки молока, чтобы испечь восемь сказочных лепешек. Давайте посмотрим на это с другой стороны. Одна столовая ложка равна 15 мл. 15 ÷ 3 = 5, поэтому – столовой ложки равно 5–10 мл, что соответствует 1–2 чайным ложкам!

Дополнительная литература по навыкам, которые вам нужны

Основы счета
Часть необходимых навыков Руководство по счету

Эта электронная книга содержит рабочие примеры и простые для понимания объяснения, чтобы показать вам, как использовать основные математические операции и начать манипулировать числами.Он также включает в себя примеры из реальной жизни, чтобы прояснить, насколько эти концепции полезны в реальной жизни.

Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.

Пошаговое руководство по продольному делению

Что такое длинное деление?

Деление в столбик — это способ решения задач деления с большими числами. По сути, это задачи деления, которые вы не можете решить в уме.

Начало работы

Одна из проблем, с которой учащиеся сталкиваются с задачами деления в столбик, — это запоминание всех шагов.Вот трюк, чтобы научиться делить в столбик. Используйте аббревиатуру DMSB, что означает:

D = разделить
M = умножить
S = вычесть
B = сбить

Эту последовательность букв может быть трудно запомнить, поэтому подумайте об аббревиатуре в контексте семьи:

Папа, мама, сестра, брат.

Напишите D M S B в углу листа, чтобы запомнить последовательность, которую вы собираетесь использовать.

Как записать

Во-первых, вы должны записать проблему в формате длинного деления.Типичная задача деления выглядит так:

Дивиденд ÷ Делитель = Частное

Чтобы записать это в формате длинного деления, это выглядит так:

Давайте попробуем довольно простой пример:

65 ÷ 5 =?

Теперь давайте запишем эту проблему в формате длинного деления:

Мы готовы использовать аббревиатуру: D M S B

Шаг 1: D для разделения

Сколько раз 5 перейдет в 65? Это слишком сложно, чтобы обдумать это, поэтому давайте разберемся на более мелкие шаги.

Первая проблема, которую вы решите в этом уравнении, — сколько раз вы можете разделить 5 на 6. Ответ: 1. Итак, вы помещаете 1 в линию частного.

Шаг 2: M для умножения

Вы умножаете свой ответ из шага 1 на ваш делитель: 1 x 5 = 5. Вы пишете 5 под 6.

Шаг 3: S для вычитания

Далее вы вычитаете. В этом случае это будет 6 — 5 = 1.

Шаг 4: B для обрушения

Последним шагом в последовательности является уменьшение следующего числа из делимого, которое в данном случае равно 5.Вы пишете 5 рядом с 1, в результате получается число 15.

Теперь вы начинаете все сначала:

Шаг 1: D для разделения

Сколько раз можно разделить 5 на 15. Ответ: 3. Итак, вы помещаете 3 в строку частного.

Шаг 2: M для умножения

Вы умножаете свой ответ из шага 1 на ваш делитель: 3 x 5 = 15. Запишите это под числом 15.

Шаг 3: S для вычитания

Теперь вычтем 15 из 15.15 — 15 = 0.

Нет необходимости в шаге 4. Проблема решена.

Получив ответ, решите задачу в обратном порядке, используя умножение (5 x 13 = 65), чтобы убедиться, что ваш ответ правильный.

K5 Learning есть несколько бесплатных рабочих листов с полными делениями для 4-го, 5-го и 6-го класса. Проверьте их в нашем центре рабочих листов по математике.

Калькулятор дробей

Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.

Правила для выражений с дробями:

Дроби — используйте косую черту «/» между числителем и знаменателем, т. Е. Для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).

Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 . 1/2
• сложение дробей и смешанные числа: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3

Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.