Сложная процентная ставка – Сложная процентная ставка

Сложная+процентная+ставка

Сложная процентная ставка

Формулы наращения

Сложная процентная ставка наращения – это процентная ставка, при которой база начисления, в отличие от простых процентов, является п е р е м е н н о й , т.е. проценты начисляются на проценты.

Также заранее оговаривается некоторый единичный промежуток начисления процентов (год, месяц, квартал и т.д.) и ставка процента i (или i% = 100i). Пусть начальная сумма долга равна P. Тогда через единичный промежуток сумма долга составит S1 = P(1+i), как и в случае простых процентов. Однако к концу 2-го единичного промежутка сумма долга составит S2 = S1(1+i) = P(1+i)2 (в отличие от формулы S2 = P(1+2i) для простых процентов. К концу 3-го периода получаем S3 = S2(1+i) = P(1+i)3. И т.д. К концу n-го единичного промежутка получаем

Итак, через n промежутков начальная сумма P увеличится в (1+i)n раз. Множитель (1+i)n называется множителем наращения. Отметим, что наращение по сложным процентам представляет рост начальной суммы по закону геометрической прогрессии, первый член которой равен P, а знаменатель 1+i.

Задача 1. Исходная сумма вклада P = 40 000 р. Процентная ставка i%=10% годовых. Определить наращѐнную по сложным процентам за 3 года, а затем сравнить ее с суммой наращения по схеме простых процентов.

Решение. Применяя формулу (1) имеем

S3,слож = P(1+i)3 = 40 000 (1+0.1)3 = 53 240 р.

Вычислим наращѐнную сумму по схеме простых процентов:

S3,пр = P(1+3i) = 40 000 (1+0.3) = 52 000 р. < 53 240 р.

Итак, в рассматриваемом случае использование сложных процентов приводит к большей наращѐнной сумме, что выгоднее вкладчику по сравнению с наращением по схеме простых процентов.

Формула наращения сложных процентов (1), выведенная для целых

положительных n, применима и для нецелых t					0: St	= P(1+i)t.
Задача 2. Какой величины S4.6	достигнет долг, равный 8 000 р., через 4.6 года
при росте по сложной ставке процента i=20% годовых.
Решение. По условию задачи P = 8 000 р. Тогда
S4.6 = P(1+i)t = 8 000(1+0.2)4.6							18 506.48.
Итак, через 4.6 года долг достигнет значения 18 506 р. 48 коп.
В том случае, когда ставка сложных процентов меняется во времени, формула
наращѐнной суммы принимает вид
S = P (1	i )n1 (1	i	2	)n 2	…(1	i	m	)n m .	(2)
	1

Здесь P – начальная сумма, nk – продолжительность k-го периода начисления процентов и ik – ставка простых процентов в периоде с номером k.

Задача 3. В договоре об обслуживании банковского вклада в течение 4-х лет зафиксирована переменная ставка сложных процентов следующим образом. В 1-й год – 6% годовых, во 2-й и 3-й год ставка одна и та же – 5% годовых, в 4-й год

– 8%. Определить величину множителя наращения за 4 года.

Решение. Пусть P – некоторая начальная сумма. По условию задачи

i1 = 0.06, i2 = i3 = 0.05, i4 = 0.08.

Обозначим i23 = 0.05. Имеем в соответствии с формулой (2):

S = P (1 i1 )1 (1 i23 )2 (1 i4 )1 = P(1+0.06)(1+0.05)2 (1+0.08).

В результате вычислений получаем значение множителя наращения:

S/P = (1+0.06)(1+0.05)2 (1+0.08) = 1.262142.

Сравнение силы роста простых и сложных процентов

При одной и той же ставке процента i наращение сложных процентов:

идет быстрее, чем простых процентов, если длина периода наращения больше единичного периода;

идет медленнее, чем простых процентов, если длина периода наращения меньше единичного периода.

Ранее было отмечено, что наращение для единичного периода одинаково, независимо от того, используется схема простых процентов или сложных.

Обоснуем сказанное. В самом деле при i > 0:

если t >1, то (1+i)t > 1+ it; если 0 < t < 1, то (1+i)t < 1+ it; если t=1, то (1+i)t = 1+ it.

Для доказательства этого факта рассмотрим функции f(t) = (1+i)t и g(t) = 1+ it. Очевидно, f(0) = g(0), f(1) = g(1) и обе функции возрастают при t 0 не только по их содержательному смыслу, но и формально ввиду положительности их производных f (t) = (1+i)t ln(1+i) и g (t) = i. В то же время производная второго порядка f(t) = (1+i)t ln2(1+i) положительна при t 0, что означает выпуклость вниз функции f(t) при t 0 (т.е. ускоренный рост). При этом функция g(t) растет линейно

(g(t) = 0).

На графике изображены функции f(t) = (1+i)t и g(t) = 1+ it в зависимости от t:

Пример. Пусть сумма P=800 наращивается по ставке i=8% простых и сложных процентов. Тогда наращѐнные суммы таковы

Промежутки начисления	0	0.5	1	1.5	2
Простые проценты	800	832	864	896	928
Сложные проценты	800	831.38	864	897.9	933.12

Для оценки своих перспектив кредитору и должнику зачастую важно знать, через сколько времени сумма ссуды возрастает в N раз при данной процентной ставке i. Для этого приравняем множитель наращения величине N, в результате чего получим:

a)для простых процентов 1 + ni = N, откуда n = (N–1) / i.

b)для сложных процентов (1 + i)n = N, откуда n = ln N / ln(1 + i).

Задача 4. Рассчитать, за сколько лет долг увеличится вдвое при ставке простых и сложных процентов, равной 4% годовых. Результаты сравнить.

Решение. По условию задачи i=0.04, N=2. Имеем

a) для простых процентов n = (N–1) / i = 1 / i, откуда n = 1/0.04 = 25 лет

b) для сложных процентов n = ln N / ln(1 + i), откуда n = ln 2/ln(1.04) 17.67 лет. Расчет по схеме сложных процентов быстрее удваивает долг.

Некоторые способы начисления процентов при дробном числе лет

В практике финансовых учреждений при дробном числе лет t проценты начисляются по-разному. Рассмотрим три основных способа начисления.

1.По формуле сложных процентов: S = P(1+i)t.

2.На основе смешанного метода, согласно которому за целое число лет начисляются сложные проценты, а за дробное – простые: S = P(1+i)n (1+bi), где t=n+b, n – целое число лет, b – дробная часть года.

3.В ряде коммерческих банков применяется правило, в соответствии с которым за отрезок времени меньше периода начисления проценты не начисляются, т.е.

S = P(1+i)n.

Задача 5. Размер ссуды, представленной на 27 месяцев, равен 100 000 р. Годовая процентная ставка равна 20%. Вычислить наращѐнную сумму указанными тремя способами.

Решение. По условию задачи срок ссуды составляет 2.25 года. Имеем следующие расчеты.

По 1-му способу: SI = 100 000(1+0.2)2 . 2 5 150 715 р. 46 коп. По 2-му способу: SII = 100 000(1+0.2)2 (1+0.25 0.2) = 151 200 р. По 3-му способу: SIII = 100 000(1+0.2)2 = 144 000 р.

Формулы дисконтирования в случае сложных процентов

При математическом дисконтировании из формулы	сложных процентов
S = P(1+i)n имеем
P = S/(1+i)n.	(3)

Задача 6. Выписать таблицу для дисконтного множителя (1+i)– n при сроке ссуды 5, 10 и 20 лет; сложная ставка наращения составляет 10% и 20%.

Решение. Результаты расчетов по формуле (3) приведены в таблице

n, лет	i=10%=0.1	i=20%=0.2
5	0.621	0.402
10	0.386	0.162
20	0.149	0.026

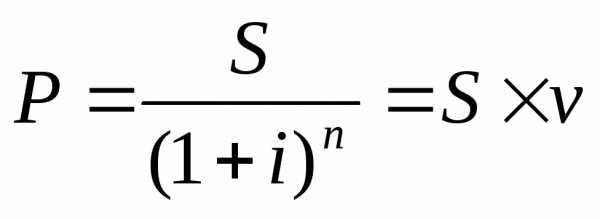
Если осуществляется дисконтирование по схеме банковского (коммерческого) учета, то изначально оговаривается учетная ставка d, 0 d<1. Она применяется не к начальной сумме, как при простой учетной ставке, а к сумме, уже дисконтированной на предыдущем промежутке времени. Размер дисконта, или учета, удерживаемого финансовым учреждением, равен

Задача 7. Вексель на сумму 20 000 р., срок платежа по которому наступает через 1.5 года, учтен по сложной процентной ставке 18% годовых. Определить сумму, полученную владельцем векселя при учете, а также соответствующий дисконт.

Решение. Здесь по условию задачи S=20 000, n=1.5, d=0.18. Тогда по формуле (4) получаем следующие результаты расчетов:

сумма, получаемая владельцем P = 20 000(1 – 0.18)1.5 14850 р. 83 коп.,

дисконт D = S – P 20 000 – 14850.83 = 5149 р. 17 коп.

studfiles.net

2.1 Сложные проценты

Раздел II. Начисление сложных процентов

Сложные проценты применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют ка-

питализацией процентов.

Формула наращения по сложным процентам

Пусть первоначальная сумма долга равна P, тогда через один год сумма долга с присоединенными процентами составит P(1+i), через 2 года P(1+i)(1+i)=P(1+i)2, через n лет — P(1+i)n. Таким образом, получаем формулу наращения для сложных процентов

где S — наращенная сумма, i — годовая ставка сложных процентов, n — срок ссуды, (1+i)n — множитель наращения.

В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т.д.). Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен P, а знаменатель (1+i).

Отметим, что при сроке n<1 наращение по простым процентам дает больший результат, чем по сложным, а при n>1 — наоборот. В этом нетрудно убедиться на конкретных числовых примерах. Наибольшее превышение суммы, наращенной по простым процентам, над суммой, наращенной по сложным процентам, (при одинаковых процентных ставках) достигается в средней части периода.

Формула наращения по сложным процентам, когда ставка меняется во времени

В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид

S = P(1+ i )n1	(1+ i )n2	…(1+ i )nk ,	(20)
1	2	k

где i1, i2,…, ik — последовательные значения ставок процентов, действующих в периоды n1, n2,…, nk соответственно.

Пример 6.

В договоре зафиксирована переменная ставка сложных процентов, определяемая как 20% годовых плюс маржа 10% в первые два года, 8% в третий год, 5% в четвертый год. Определить величину множителя наращения за 4 года.

Решение.

(1+0,3)2(1+0,28)(1+0,25)=2,704

studfiles.net

Переменная сложная процентная ставка

Переменная сложная процентная ставка – ставка, применяемая к активу с присоединенными к нему за предыдущий период процентами. Принцип ее расчета состоит в прибавлении суммы процентов к базе в конце установленного времени. При этом применяется разная процентная ставка, которая варьируется в зависимости от конкретного периода.

Действие сложной переменной ставки проявляется в долгосрочных инвестициях, имеющих множество периодов начисления процентов.

Специфика применения сложной переменной процентной ставки

Сложные переменные ставки используются для снижения влияния на капитал тех переменных факторов, которые имеют значение для распорядителя средств. Самым распространенным вариантом считается привязка процента к ставке рефинансирования центрального банка, которая является индикатором средней доходности капитала в стране.

Cложные переменные ставки используются с целью привлечения инвестора, так как ее доходность выше, чем у простой ставке, а сам процент может увеличиваться с каждым последующим периодом начисления. Этот метод используют банки при необходимости привлечения средств вкладчиков на длительный период.

В обратной ситуации, когда требуется разместить ресурсы на возвратной основе, кредитор может заинтересовать заемщика снижением ставок через некоторые промежутки времени. Доходность в этом случае обеспечивается за счет сложной ставки и первоначального применения уровня доходности выше среднего.

Изменение и порядок расчета сложных переменных процентных ставок

В зависимости от поставленных задач переменная ставка в разных периодах может изменяться следующим образом:

• пропорционально изменению привязанного к ней финансового параметра;
• иметь прогрессивный (регрессивный) характер, т. е. увеличиваться или уменьшаться с каждым последующим периодом;
• принимать значения, изначально установленные для каждого периода.

При известном значении переменных ставок, например, при включении их в условия договора, для инвестора имеет смысл определить наращенную сумму капитала (K), которая будет равна:

K = K_o * П (1+R_t) ^n(t), где

K_o – первоначальный размер актива;
П– произведение;
R_t – процентная ставка в период времени t;
n(t) – количество периодов t.

Периоды начисления могут быть неравномерными, поэтому целесообразно знать долю каждого из них (d) в общем сроке оборота капитала (T):

d = t / T

Также расчеты из области финансовой математики позволяют оценить общую доходность актива, т. е. найти среднюю ставку в конкретном периоде (R):

R = П (1+R_t) ^d(t) – 1, где

R_t – процентная ставка в период времени t;
d(t) – доля периода t.

На предварительном этапе оценки доходности вложений, предусматривающих использование сложной ставки, можно воспользоваться «правилом 72». Оно позволяет с небольшой погрешностью определить срок, через который сумма актива удвоится. Для этого необходимо число 72 разделить на среднюю ставку процента за период, в итоге получим количество периодов.

Преимущества использования сложной переменной процентной ставки

Опираясь на опыт западных стран, российские банки широко применяют метод сложных переменных ставок. Особенно распространен он в сфере ипотечного кредитования. Причем размер ставки может изменяться сразу, а может быть фиксированным в течение конкретного срока.

Для выбора оптимального пути заемщику необходимо оценить критерии и периодичность изменения ставки, а также общий срок обязательства. Сделать это можно путем вычислений, указанных выше.

utmagazine.ru

Простые и сложные процентные ставки

Как уже отмечалось выше (см. Базовые концепции финансового менеджмента), временная стоимость денег может быть выражена несложной зависимостью (формулой) математического дисконтирования: PV = FV/(1 + r), (2.1)

где через PV обозначена текущая (дисконтированная) стоимость будущего денежного потока; через FV – будущая (наращенная) стоимость текущего денежного потока; через r – ставка доходности, соответствующая оценке инвестором уровня риска. Формула, обратная формуле (2.1), носит название формулы наращения: FV = PV(1 + r). (2.2)

В формулах (2.1) и (2.2) ставка r представляет собой периодическую ставку, соответствующую одному периоду времени между текущим и будущим денежными потоками (в качестве такого периода может выступать год, квартал, месяц и др.) Если таких периодов до будущего платежа несколько, то формулы (2.1) и (2.2) примут соответственно вид PV = FV/(1 + r)ⁿ, (2.1′)

FV = PV(1 + r)ⁿ. (2.2′)

Формула (2.2′) выражает начисление процентов по сложной ставке. При этом процентный доход начисляется не только на основную сумму PV, но и на ранее начисленные проценты. В финансовом менеджменте использование сложного процента означает неявное предположение о реинвестировании получаемого дохода под действующую ставку доходности.

В некоторых случаях используется и ставка простого процента, начисляемая по формуле

FV = PV(1 + пr). (2.3)

При этом проценты начисляются только на основную сумму PV. Использование простых процентов правомерно в случаях, когда начисление производится за период, меньший, чем промежуток времени между соседними начислениями (выплатами) дохода.

Внутригодовые процентные начисления

В современной практике достаточно часто встречаются случаи, когда начисление процентов по некоторой номинальной годовой процентной ставке r осуществляется чаще, чем один раз в год. В частности, таким образом обычно начисляются проценты по банковским вкладам. В этом случае проценты, начисленные по подпериодам в соответствии с периодичностью начисления, будут реинвестироваться под ставку, равную номинальной годовой деленной на количество периодов начисления в году. Наращенная стоимость в таком случае будет иметь вид FV = PV(1 + r/m)^mn, (2.4)

где m — количество начислений в году, r — номинальная годовая процентная ставка, n — количество лет. Очевидно, что чем чаще происходит начисление процентов при одной и той же номинальной годовой ставке, тем выше будет начисленная сумма. При этом если устремить число начислений m к бесконечности, то есть продолжительность периода начисления – к нулю, то формула (2.4) примет вид²

FV = PV℮^{r n}, (2.4′)

где ℮ — основание натурального логарифма. Начисление процентов по формуле (2.4′) носит название непрерывного и используется в теории управления инвестиционным портфелем.

Эффективная годовая процентная ставка

Управленческая практика достаточно часто требует сравнения эффективности различных схем начисления процентов. Удобным инструментом для проведения подобных сравнений служит так называемая эффективная годовая процентная ставка, которую обычно обозначают R. Эффективная годовая ставка представляет собой процентную ставку с периодом начисления один год, эффект начисления которой эквивалентен начислению номинальной или периодической процентной ставки m раз в год. Соответственно эффективная годовая ставка R может быть определена из формулы

1 + R = (1 + r/m)^m. (2.5)

Заметим, что в правой части формулы (2.5) вместо отношения r/m может стоять процентная ставка за соответствующий внутригодовой период.

studfiles.net

Простая и сложная процентные ставки

«Прямые» формулы

«Обратные» формулы

Переменная процентная ставка и реинвестирование вкладов

Пусть срок долга имеет этапов, длина которых равна , ,

— при схеме простых процентов

— при схеме простых процентов

Примеры:

1. В контракте предусмотрено начисление а) простого, б) сложного процента в таком порядке: в первом полугодии по годовой процентной ставке 0,09, потом в следующем году ставка уменьшилась на 0,01, а в следующих двух полугодиях увеличилась на 0,005 в каждом из них. Найти величину наращенного вклада в конце срока, если величина первоначального вклада равна $800.

,

,

,

,

а)

б)

Рыночная процентная ставка как важнейший макроэкономический показатель

Важным макроэкономическим показателем выступает процентная ставка. Процентная ставка — это плата за деньги, предоставляемые в кредит. Были времена, когда законом не допускалось вознаграждение за то, что неизрасходованные, заемные деньги давали в заем. В современном мире широко пользуются кредитами, за пользование которыми устанавливается процент. Поскольку процентные ставки измеряют издержки использования денежных средств предпринимателями и вознаграждение за неиспользование денег потребительским сектором, то уровень процентных ставок играет значительную роль в экономике страны в целом.

Очень часто в экономической литературе пользуются термином «процентная ставка», хотя существует множество процентных ставок. Дифференциация процентных ставок связана с риском, на который идет заимодатель. Риск возрастает с увеличением срока кредита, так как становится выше вероятность того, что деньги могут потребоваться кредитору раньше установленной даты возврата ссуды, соответственно повышается процентная ставка. Она увеличивается, когда за кредитом обращается малоизвестный предприниматель. Мелкая фирма уплачивает более высокую процентную ставку, чем крупная. Для потребителей процентные ставки также варьируются.

Однако как бы ни отличались ставки процента, все они находятся под воздействием рыночного механизма: если предложение денег уменьшается, то процентные ставки увеличиваются, и наоборот. Именно поэтому рассмотрение всех процентных ставок можно свести к изучению закономерностей одной процентной ставки и в дальнейшем оперировать термином «процентная ставка»

Различают номинальные и реальные процентные ставки

Реальная процентная ставка определяется с учетом уровня инфляции. Она равна номинальной процентной ставке, которая устанавливается под воздействием спроса и предложения, за вычетом уровня инфляции:

= i — %ΔP

§ — реальная процентная ставка;

§ — номинальная процентная ставка;

§ — общий уровень цен.

Если, например, банк предоставляет кредит и взимает при этом 15%, а уровень инфляции составляет 10%, то реальная процентная ставка равна 5% (15% — 10%).

Способы начисления процентов:

Декурсивный способ	проценты начисляются в конце каждого интервала начисления	ссудный процент
Антисипативный способ	проценты начисляются в начале каждого интервала начисления	учетная ставка

§ — проценты за весь срок ссуды

§ — первоначальная сумма долга

§ — наращенная сумма, то есть сумма в конце срока

§ — ставка наращения процентов

§ — срок ссуды

	Простая процентная ставка	Сложная процетная ставка
Начисленные за весь срок проценты:
Наращенная сумма

Структура процентной ставки

 

Из чего складывается и зависит величина процентной ставки? Издревле этот вопрос задавался бесчисленное множество раз. Ответы на него давались разные, однако после работ И. Фишера и Дж. М. Кейнса выполненных в тридцатые годы прошлого столетия по данному вопросу появилось в определенной степени «общепринятое мнение», которое получило развитие в 50-60-е гг. в работах Г. Марковица, У. Шарпа и других.

 

Итак, что мы знаем о структуре процентной ставки? Мы знаем, что согласно И. Фишеру зависимость между номинальной и реальной ставками процента описывается уравнением:

 

(1)

 

где r_n – номинальная ставка процента,

r_r — реальная ставка процента,

i – уровень инфляции за период.

 

Мы также знаем «по Марковицу и Шарпу», что в реальной инвестиционной деятельности процентная ставка является комбинацией двух величин – ставки процента в отсутствие риска и премии за наличие риска:

(2)

 

где r – ставка процента характерная для будущих денежных потоков проекта (актива) имеющего определенный риск инвестирования,

r_f— ставка процента по безрисковым вложениям,

p — премия за риск инвестирования в подобные проекты (активы)[1] .

Таким образом, из работ классиков известно, что уровень процентной ставки является функцией очищенной от инфляции безрисковой ставки, инфляции и компенсации (премии) за риск:

 

(3)

где r_n– номинальная процентная ставка рискового проекта (актива),

r_fr — очищенная от инфляции безрисковая ставка процента.

 

Можно ли дальше расщепить какую-либо из компонент входящих в выражение (3)?

 

Конечно, можно! Самые наглядные примеры – модель кумулятивного построения (build up) и многофакторные модели арбитражного ценообразования (APT). Здесь наступил момент, когда автор настоящей статьи считает возможным сделать переход от «объективно-созерцательного» к «пристрастно-субъективному» изложению материала. По мнению автора, модель кумулятивного построения появилась на свет не от хорошей жизни, а из принципа заполнения вакуума. Идея проста: взяли исторически наблюдаемую максимальную премию как максимальное превышение рисковых ставок над безрисковыми и поделили ее на равное число пришедших в голову факторов риска. При реально «зафиксированных» максимальных рисковых ставках на уровне 35%, среднем уровне безрисковой ставки 5% и шести факторах риска (менеджмент, территориальная товарная, снабженческо-сбытовая диверсифицированность и т.п.) получилось, что на каждый компонент риска может приходиться максимум (35-5)/6 = 5%, а минимум – 0%. Все бы ничего, но как-то уж слишком много вопросов возникает к такому упрощенному подходу:

· Почему используются именно эти факторы риска, а не другие?

· Почему по умолчанию полагается, что степень влияния каждого из этих факторов ограничивается максимум пятью процентами?

· Как корректно градуировать каждый из входящих в модель факторов по системе «плохо-хорошо», и какова точность результата получаемого на выходе модели?

 

Говоря о других многофакторных моделях оценки процентных ставок (ставок дисконтирования), построенных на базе использования корреляционно-регрессионного анализа, автор настоящей статьи находит их значительно более привлекательными в части точности и обоснованности. Однако и у них есть свои минусы: таких моделей слишком много, используемые в них факторы зачастую слишком специфичны, а использованные для их синтеза данные охватывают различные временные ряды, полученные в разное время на различных географических рынках. Все это привело к тому, что на сегодняшний день на рынке нет одной-двух общепринятых моделей такого плана. В этой связи попробуем предложить вариант такой модели, основанной на минимально возможном количестве факторов. Забегая вперед, отметим, что по большому счету это не так сложно: необходимо «всего-то» корректно объяснить, что такое безрисковая ставка и какие могут быть риски инвестирования.

Безрисковая ставка

Безрисковая ставка – это ставка процента в отсутствие рисков. Обычно в качестве наблюдаемых безрисковых ставок используются процентные ставки по правительственным облигациям. Однако следует иметь в виду, что облигации подвержены инфляционному риску (наблюдаются номинальные, а не реальные ставки) и они чуть менее ликвидны, чем деньги. К тому же, в процентных ставках облигаций некоторых стран «зашит» риск дефолта (достаточно вспомнить опыт России образца 1998 г.). Если убрать все возможные риски (инфляцию, неликвидность, дефолт), то сухим остатком будет абсолютно безрисковая ставка (обозначим ее r_nf). Какова природа этой ставки? Эта ставка зиждется на двух взаимодополняющих факторах.

Во-первых, деньги сегодня стоят дороже, чем эти же деньги завтра (послезавтра и в последующие периоды). Если вы кому-то даете взаймы на определенный срок, значит, скорее всего, в течение этого срока вы будете терпеть определенные лишения (меньше тратить на повседневную жизнь, откладывать некоторые покупки на потом).

Во-вторых, нельзя скидывать со счетов ростовщический фактор: если кто-то просит у вас денег взаймы, значит, идя на это, заемщик (берущий деньги) рассчитывает на то, что получив и затем возвратив деньги в назначенный срок, он получит выгоду. Само собой разумеется, осознаете это и вы, и со своей стороны вполне резонно рассчитываете на «справедливую аннексию» части полученной заемщиком выгоды в свою пользу («делиться надо!» — А.Я. Лившиц).

 

 

Риски инвестирования

Какие риски поджидают инвестора вкладывающего средства в реальный проект или актив? Существует множество всевозможных рисков, но самые общие из них подразделяются на риск невозврата и риск неликвидности.

Риск невозврата может возникать в двух ситуациях:

1. когда проект (актив, или займополучатель) по объективным причинам не в состоянии вернуть вложенные деньги по причине банкротства, дефолта, халатности финансово-хозяйственной деятельности или форс-мажорных обстоятельств («хочет, но не может»).

2. когда займополучатель сознательно не выполняет обязательств по возврату денежных средств («может, но не хочет»).

Риск неликвидности связан с риском упущенных возможностей. Рассмотрим две ситуации. Предположим, инфляция отсутствует и в обозримом будущем не предвидится.

1. Инвестор покупает неденежный актив, приносящий ему невысокий процент, и у него почти не остается свободных денежных средств, за исключением средств на текущие расходы. Тогда, если ему вдруг представится возможность срочной выгодной покупки хорошего, но дорогого другого актива, он может упустить эту возможность, поскольку, во-первых, другой актив, как правило, нельзя обменять на имеющийся у инвестора актив, а можно купить только за деньги; во-вторых, срок реализации имеющегося актива может превысить время, в течение которого еще можно приобрести другой актив.

2. Инвестор обдумывает дать взаймы денежную сумму абсолютно надежному заемщику на определенный срок под невысокий процент, но не решается на это из-за сомнений типа: «А что, если за это время я упущу какие-либо потенциальные возможности из-за нехватки наличных денег? В конце-концов, могу просто не дожить до обещанного момента возврата».

Рассмотренные примеры объединяет возможность того, что ущерб от меньшей ликвидности неденежных активов может превысить генерируемые ими доходы. Поэтому для компенсации риска неликвидности следует применять премию за неликвидность — p_il:

 

(4)

 

или

 

(5)

 

где p_il – рыночная премия за риск неликвидности,

i_{срочная} — процентная ставка по срочным депозитам (1 год), или срочным кредитам (в этом случае i_{срочная} берется с отрицательным знаком),

i_{до востребования} — процентная ставка по депозитам до востребования, или кредитам с возможностью досрочного погашения (в этом случае i_{до востребования} берется с положительным знаком),

i_min — минимальная депозитная ставка, при которой возникает эффект ликвидной ловушки (когда владельцев денежных средств не прельщает перспектива суеты и снижения ликвидности своих активов ради символических 2-3% годовых).

Выражения (4) и (5) являются одними из возможных способов оценки премии за пониженную ликвидность.

Кроме рыночной величины премии за неликвидность, для каждого инвестора может быть рассчитана инвестиционная стоимость премии за риск неликвидности — p_INVil:

 

 

(6)

 

где L_c – издержки ликвидности денежных средств, определяемые по формулам авторской модели инвестиционной стоимости ликвидности актива,

L_nc — издержки ликвидности неденежного актива (проекта), определяемые по формулам вышеуказанной модели.



infopedia.su

Сложная процентная ставка — это… Что такое Сложная процентная ставка?



Сложная процентная ставка

Сложная процентная ставка

Сложная процентная ставка — процентная ставка, которая применяется к сумме с процентами, начисленными в предыдущем периоде. Обычно сложные процентные ставки используются для долгосрочных ссуд со сроком более года.
При сложной процентной ставке процентный платеж в каждом расчетном периоде добавляется к капиталу предыдущего периода, а процентный платеж в последующем периоде начисляется уже на эту наращенную величину первоначального капитала.

См. также:  Сложные процентные ставки   Процентные ставки  

Финансовый словарь Финам.

.

• Сложная предметная рубрика
• Сложная структура капитала

Смотреть что такое «Сложная процентная ставка» в других словарях:

• СЛОЖНАЯ ПРОЦЕНТНАЯ СТАВКА — процентная ставка, которая применяется к сумме с процентами, начисленными в предыдущем периоде. Обычно сложные процентные ставки используются для долгосрочных ссуд со сроком более года. При сложной процентной ставке процентный платеж в каждом… …   Словарь бизнес-терминов

• Сложная процентная ставка — …   Википедия

• Переменная сложная процентная ставка — процентная ставка, которая применяется к сумме с процентами, начисленными в предыдущем периоде; но которая может изменяться в определенные моменты времени в течение срока ссуды. См. также: Сложные процентные ставки Финансовый словарь Финам …   Финансовый словарь

• Учётная ставка — финансовый термин, финансовая категория, употребляемая для характеристики следующих процессов, связанных с кредитованием[1]: Под учётной ставкой понимается процентная ставка, по которой Центральный банк страны предоставляет кредиты коммерческим… …   Википедия

• Учетная ставка — Учётная ставка (англ. Discount rate) это сумма, указанная в процентном выражении к величине денежного обязательства (векселя), которую взимает приобретатель обязательства. Фактически, учётная ставка это цена, взимаемая за приобретение… …   Википедия

• Экономика страны — (National economy) Экономика страны это общественные отношения по обеспечению богатства страны и благосостояния ее граждан Роль национальной экономики в жизни государства, сущность, функции, отрасли и показатели экономики страны, структура стран… …   Энциклопедия инвестора

• Макроэкономическая статистика — (Macroeconomic statistics) Понятие макроэкономической статистики, виды статистических показателей Информация о понятии макроэкономической статистики, виды статистических показателей Содержание >>>>>>>>>>>> …   Энциклопедия инвестора

• Банк — (Bank) Банк это финансово кредитное учреждение, производящее операции с деньгами, ценными бумагами и драгоценными металлами Структура, деятельность и денежно кредитной политика банковской системы, сущность, функции и виды банков, активные и… …   Энциклопедия инвестора

• Депозит — (Deposit) Содержание Содержание Определение Размещение на депозите Понятие и правовая природа банковского вклада Нюансы российской банковской практики Депозитный сертификат Депози́т (банковский ) — это сумма , помещённая в на… …   Энциклопедия инвестора

• Центральный банк — (Central bank) Центральный банк это орган проведения денежно кредитной политики Информация о деятельности, политике, функциях, операциях Центрального банка, ставка рефинансирования Содержание >>>>>>>>>>>>> …   Энциклопедия инвестора

dic.academic.ru

Простые и сложные проценты

     На сегодняшний день наиболее простой по энергозатратам способ получения прибыли – это инвестиции. Особых усилий прикладывать не нужно, если имеются свободные денежные средства, их нужно положить в банк и спокойно ждать, когда сумма вклада увеличится до желаемого размера. Однако, есть здесь и свои риски. Не будем говорить о самых страшных, когда банк может просто обанкротиться. Риск существует и при неправильном или плохо просчитанном вложении средств. В этом случае вкладчик рискует не получить желаемой прибыли или получить ее в меньшем размере. В последнее время очень популярен инвестиционный заработок в интернете.

 

     Основной операцией в инвестиционной и экономической деятельности является операция начисления процентов. Что же это за операция? Поясним на конкретном примере. Например, когда вкладчик открывает в банке депозит, то через определенный период времени средства возвращаются к нему с прибылью. Вполне логично, что, получив прибыль, вкладчик захочет еще раз провести ту же операцию, а возможно, и несколько раз. Вот здесь перед ним и возникают такие понятия, как простые и сложные проценты. Какой из этих показателей более выгодный. Попробуем разобраться.

 Простые и сложные проценты

С повторным или неоднократным вложением денег регулярно сталкиваются не только профессиональные инвесторы или рядовые вкладчики, но и те, кто работают на валютных биржах. И если, скажем, при вложении денег в банк депозит приносит прибыль через определенное время, то при инвестировании в валютной сфере прибыль или наоборот, убыток, появляются после проведения каждой операции. Поэтому и просчитывать возможную прибыль здесь необходимо более тщательно, чем при банковских вкладах.

Итак, что же такое простые и сложные проценты?

 

Под простым процентом понимается прибыль, которая начисляется только на первоначальную сумму за каждый определенный промежуток времени.

 

Например, владелец кладет в банк депозит в размере 5000$, ставка 20% годовых. Простой процент будет приносить прибыль в размере 1000$ каждый год, независимо от того, какая сумма уже накопилась на счету за это время и независимо от того, оставляет он проценты в банке или регулярно снимает их.
То есть при схеме простого процента база начисления прибыли всегда равна первоначальной вложенной сумме. Этот вид начисления процентов используется при специальных банковских депозитах, а также при оформлении кредита. Если инвестор намерен периодически выводить прибыль со своего счета, ему также будет предложен депозит с начислением простого процента.

 

Сложный процент – несколько иная форма начисления процентов по вкладу. Прибыль здесь начисляется не на первоначальный взнос, а на целую сумму, вместе с уже начисленными процентами, которая в данный момент находится на счету у вкладчика. То есть, по истечении каждого периода сумма, на которую начисляется прибыль, пропорционально увеличивается.
Возьмем тот же пример с депозитом в размере 5000$ и ставкой 20% в год. В первый год проценты будут начисляться с 5000$, и прибыль составит 1000$. В следующем году процент уже будет начисляться с 6000$ и так далее, пока вкладчик не примет решение вывести депозит со счета.
Схема сложного процента используется на валютных и других биржах, потому что в этой области постоянно меняются суммы вложений. Также эта схема удобна, если инвестору нет необходимости выводить прибыль после окончания определенного периода. В этом случае деньги «работают» на своего владельца постоянно. Еще один пример, когда лучше использовать сложный процент, это когда планируется периодически или регулярно пополнять сумму вклада.

 
 

 

При первом знакомстве кажется, что между простыми и сложными процентами не так уж много отличий. Однако, преимущество сложных процентов очевидно, и с течением времени оно становится более явным. При использовании схемы сложного процента можно увеличить сумму инвестиции в несколько раз. Приведенные ниже примеры покажут наглядно, насколько выгоднее использовать сложные проценты. А чтобы использовать их грамотно, нужно уметь считать их правильно. В этом помогут следующие формулы.

 

Как рассчитать сложные проценты

 

Для того, чтобы просчитать, как приумножить деньги сложными процентами и какую прибыль принесет банковский вклад за несколько лет, нужно знать следующие показатели:

 

• первоначальный размер вклада К0

• ставка дохода R

• количество лет, за которые нужно просчитать доход n

• конечная сумма К

По следующей формуле можно рассчитать эту самую конечную прибыль:
К=К0*(1+R)n
А просчитав размер конечной суммы, легко можно установить размер прибыли – это разница между конечной и первоначальной суммами.
При помощи приведенной выше формулы всегда можно просчитать, какой результат принесет в будущем инвестиция.

 

     Иногда возникают ситуации, когда нужно, наоборот, вычислить стартовую сумму вклада. Тогда эту формулу нужно преобразовать вот в такой вид:
K0=K/(1+R)n
С помощью формулы можно узнать и такой параметр, как процентная ставка. Эта информация требуется, когда инвестор, к примеру, хочет узнать, какую ставку ему выбрать, и на какой период нужно сделать вклад, чтобы получить конкретную прибыль.
Формула вычисления сложных процентов:
R=n?K/K0-1
А вот по этой формуле высчитывается период времени, на который нужно вложить средства, чтобы получить определенную желаемую прибыль:
n=log1+R*K/K0

 

     При расчете срока вклада для получения определенной прибыли следует учитывать тот факт, что практически все банки используют целые периоды. То есть, если расчет по формуле показал, что средства для получения конкретной прибыли нужно вложить на 3 года и 9 месяцев, то нужно понимать, что в реальности необходимо будет положить депозит на 4 полных года.
Есть и более сложные примеры расчетов прибыли по сложным процентам. К таким примерам относятся вклады с возможностью пополнения. Допустим, у вкладчика есть депозит, который он ежемесячно пополняет определенной суммой. Как же рассчитать, какую прибыль он получит с такого депозита?

Здесь уже простой формулой расчета не обойтись, нужны более сложные механизмы.
Рассмотрим эту задачу на конкретном примере: вкладчик положил на счет 1000$ и каждый месяц добавляет к нему 50$. Допустим, процентная ставка составляет 1% в месяц. Для подсчета конечной суммы через пять лет нужно подставить в приведенные выше формулы показатели за каждый период, т.е. за 60 месяцев. Ведь сумма увеличивается не только за счет процентов, но и за счет ежемесячного добавления. При данных условиях по итогам первого месяца сумма на счету составила 1010$. К ней добавились еще 50$. То есть, для расчета конечной суммы во второй месяц процент нужно начислять уже на 1060$. И так далее, до окончания задуманного срока.

 

 

 

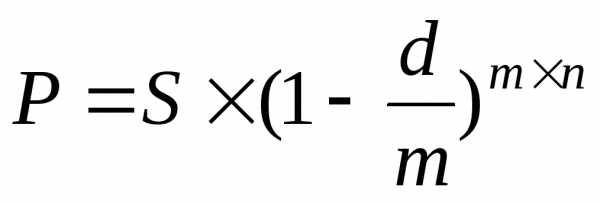
Конечно, каждый раз производить такие вычисления довольно сложно, особенно тем, кто не владеет достаточными познаниями в математике. Да и таблицы такие каждый раз не насоставляешься. Поэтому специально для вычисления сложных процентов по вкладам можно разработать свой калькулятор например в таблице excel.

 

Итак, очевидна разница между простыми и сложными процентами. Однако, следует отметить, что и схема простых процентов при грамотном ее использовании также может принести довольно хорошие результаты в виде прибыли. Более того, простые проценты являются единственным приемлемым вариантом, когда вкладчик нуждается в регулярном выводе средств со счета. Тогда он просто выводит сумму прибыли, накопившейся за месяц, полгода или год. Тогда как сложные проценты более приемлемы в случае долгосрочного вклада и повторного реинвестирования.

Читайте также: Фандрайзинг

 

trey.pro